In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold. It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is flat, i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.
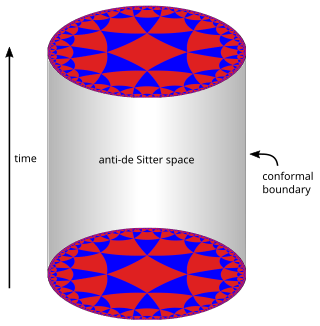
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.

Euler's Disk, invented between 1987 and 1990 by Joseph Bendik, is a trademark for a scientific educational toy. It is used to illustrate and study the dynamic system of a spinning and rolling disk on a flat or curved surface. It has been the subject of several scientific papers.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.

A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical tone. Vibrating strings are the basis of string instruments such as guitars, cellos, and pianos.
In physics, the Polyakov action is an action of the two-dimensional conformal field theory describing the worldsheet of a string in string theory. It was introduced by Stanley Deser and Bruno Zumino and independently by L. Brink, P. Di Vecchia and P. S. Howe in 1976, and has become associated with Alexander Polyakov after he made use of it in quantizing the string in 1981. The action reads:
The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
In probability theory and statistics, the normal-gamma distribution is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision.
In the differential geometry of surfaces, a Darboux frame is a natural moving frame constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space. It is named after French mathematician Jean Gaston Darboux.
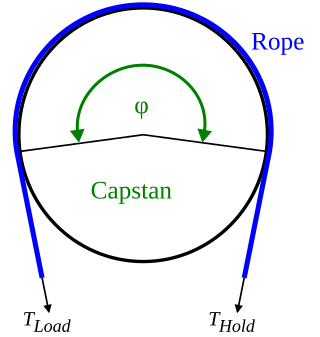
The capstan equation or belt friction equation, also known as Euler-Eytelwein formula, relates the hold-force to the load-force if a flexible line is wound around a cylinder.
In mechanics and geodynamics, a critical taper is the equilibrium angle made by the far end of a wedge-shaped agglomeration of material that is being pushed by the near end. The angle of the critical taper is a function of the material properties within the wedge, pore fluid pressure, and strength of the fault along the base of the wedge.
The Grey atmosphere is a useful set of approximations made for radiative transfer applications in studies of stellar atmospheres based on the simplified notion that the absorption coefficient of matter within a star's atmosphere is constant—that is, unchanging—for all frequencies of the star's incident radiation.
Contact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction. Frictional contact mechanics is the study of the deformation of bodies in the presence of frictional effects, whereas frictionless contact mechanics assumes the absence of such effects.
In orbital mechanics, Gauss's method is used for preliminary orbit determination from at least three observations of the orbiting body of interest at three different times. The required information are the times of observations, the position vectors of the observation points, the direction cosine vector of the orbiting body from the observation points and general physical data.
The fracture of soft materials involves large deformations and crack blunting before propagation of the crack can occur. Consequently, the stress field close to the crack tip is significantly different from the traditional formulation encountered in the Linear elastic fracture mechanics. Therefore, fracture analysis for these applications requires a special attention. The Linear Elastic Fracture Mechanics (LEFM) and K-field are based on the assumption of infinitesimal deformation, and as a result are not suitable to describe the fracture of soft materials. However, LEFM general approach can be applied to understand the basics of fracture on soft materials. The solution for the deformation and crack stress field in soft materials considers large deformation and is derived from the finite strain elastostatics framework and hyperelastic material models.

























