
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations that won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagrams, as would [Wilczek's] calculations that established a route to production and observation of the Higgs particle."

In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.

A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called analysis. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time.
In mathematics, specifically functional analysis, Mercer's theorem is a representation of a symmetric positive-definite function on a square as a sum of a convergent sequence of product functions. This theorem, presented in, is one of the most notable results of the work of James Mercer (1883–1932). It is an important theoretical tool in the theory of integral equations; it is used in the Hilbert space theory of stochastic processes, for example the Karhunen–Loève theorem; and it is also used to characterize a symmetric positive semi-definite kernel.

In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group, the finite abelian groups, and the additive group of the integers, the real numbers, and every finite dimensional vector space over the reals or a p-adic field.

In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In mathematics, a positive-definite function is, depending on the context, either of two types of function.

In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Roughly speaking, this means that if two functions and in the RKHS are close in norm, i.e., is small, then and are also pointwise close, i.e., is small for all . The converse does not need to be true. Informally, this can be shown by looking at the supremum norm: the sequence of functions converges pointwise, but do not converge uniformly i.e. do not converge with respect to the supremum norm.
In mathematics, particularly in functional analysis, a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a fixed Hilbert space. Projection-valued measures are formally similar to real-valued measures, except that their values are self-adjoint projections rather than real numbers. As in the case of ordinary measures, it is possible to integrate complex-valued functions with respect to a PVM; the result of such an integration is a linear operator on the given Hilbert space.
In mathematics, the Hamburger moment problem, named after Hans Ludwig Hamburger, is formulated as follows: given a sequence, does there exist a positive Borel measure μ on the real line such that
A quasiprobability distribution is a mathematical object similar to a probability distribution but which relaxes some of Kolmogorov's axioms of probability theory. Quasiprobabilities share several of general features with ordinary probabilities, such as, crucially, the ability to yield expectation values with respect to the weights of the distribution. However, they can violate the σ-additivity axiom: integrating over them does not necessarily yield probabilities of mutually exclusive states. Indeed, quasiprobability distributions also have regions of negative probability density, counterintuitively, contradicting the first axiom. Quasiprobability distributions arise naturally in the study of quantum mechanics when treated in phase space formulation, commonly used in quantum optics, time-frequency analysis, and elsewhere.
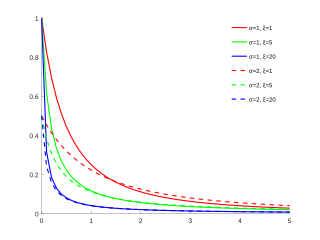
In statistics, the generalized Pareto distribution (GPD) is a family of continuous probability distributions. It is often used to model the tails of another distribution. It is specified by three parameters: location , scale , and shape . Sometimes it is specified by only scale and shape and sometimes only by its shape parameter. Some references give the shape parameter as .
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T || ≤ 1. This notion is a special case of the concept of a contraction mapping, but every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators. The theory of contractions on Hilbert space is largely due to Béla Szőkefalvi-Nagy and Ciprian Foias.
Fourier and related algebras occur naturally in the harmonic analysis of locally compact groups. They play an important role in the duality theories of these groups. The Fourier–Stieltjes algebra and the Fourier–Stieltjes transform on the Fourier algebra of a locally compact group were introduced by Pierre Eymard in 1964.

In mathematics, Hilbert spaces allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space.
In mathematics, the Pettis integral or Gelfand–Pettis integral, named after Israel M. Gelfand and Billy James Pettis, extends the definition of the Lebesgue integral to vector-valued functions on a measure space, by exploiting duality. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure. The integral is also called the weak integral in contrast to the Bochner integral, which is the strong integral.
In mathematics, a positive harmonic function on the unit disc in the complex numbers is characterized as the Poisson integral of a finite positive measure on the circle. This result, the Herglotz-Riesz representation theorem, was proved independently by Gustav Herglotz and Frigyes Riesz in 1911. It can be used to give a related formula and characterization for any holomorphic function on the unit disc with positive real part. Such functions had already been characterized in 1907 by Constantin Carathéodory in terms of the positive definiteness of their Taylor coefficients.
In mathematics, the Poisson boundary is a measure space associated to a random walk. It is an object designed to encode the asymptotic behaviour of the random walk, i.e. how trajectories diverge when the number of steps goes to infinity. Despite being called a boundary it is in general a purely measure-theoretical object and not a boundary in the topological sense. However, in the case where the random walk is on a topological space the Poisson boundary can be related to the Martin boundary which is an analytic construction yielding a genuine topological boundary. Both boundaries are related to harmonic functions on the space via generalisations of the Poisson formula.
In mathematics, Wiener's lemma is a well-known identity which relates the asymptotic behaviour of the Fourier coefficients of a Borel measure on the circle to its atomic part. This result admits an analogous statement for measures on the real line. It was first discovered by Norbert Wiener.































