
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.

In mathematics, a filter or order filter is a special subset of a partially ordered set (poset), describing "large" or "eventual" elements. Filters appear in order and lattice theory, but also topology, whence they originate. The notion dual to a filter is an order ideal.
In mathematical logic, model theory is the study of the relationship between formal theories, and their models. The aspects investigated include the number and size of models of a theory, the relationship of different models to each other, and their interaction with the formal language itself. In particular, model theorists also investigate the sets that can be defined in a model of a theory, and the relationship of such definable sets to each other. As a separate discipline, model theory goes back to Alfred Tarski, who first used the term "Theory of Models" in publication in 1954. Since the 1970s, the subject has been shaped decisively by Saharon Shelah's stability theory.
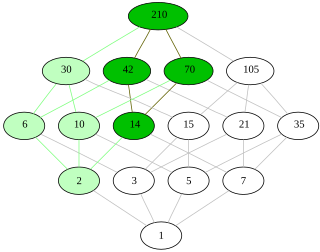
In the mathematical field of order theory, an ultrafilter on a given partially ordered set is a certain subset of namely a maximal filter on that is, a proper filter on that cannot be enlarged to a bigger proper filter on
In the mathematical discipline of set theory, forcing is a technique for proving consistency and independence results. Intuitively, forcing can be thought of as a technique to expand the set theoretical universe to a larger universe by introducing a new "generic" object .
In mathematics, especially in order theory, a Galois connection is a particular correspondence (typically) between two partially ordered sets (posets). Galois connections find applications in various mathematical theories. They generalize the fundamental theorem of Galois theory about the correspondence between subgroups and subfields, discovered by the French mathematician Évariste Galois.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
In mathematics, in set theory, the constructible universe, denoted by , is a particular class of sets that can be described entirely in terms of simpler sets. is the union of the constructible hierarchy. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this paper, he proved that the constructible universe is an inner model of ZF set theory, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axioms of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In mathematical order theory, an ideal is a special subset of a partially ordered set (poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
In the mathematical field of set theory, Martin's axiom, introduced by Donald A. Martin and Robert M. Solovay, is a statement that is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, but it is consistent with ZFC and the negation of the continuum hypothesis. Informally, it says that all cardinals less than the cardinality of the continuum, , behave roughly like . The intuition behind this can be understood by studying the proof of the Rasiowa–Sikorski lemma. It is a principle that is used to control certain forcing arguments.
In mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum. Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing. Every Boolean algebra A has an essentially unique completion, which is a complete Boolean algebra containing A such that every element is the supremum of some subset of A. As a partially ordered set, this completion of A is the Dedekind–MacNeille completion.
In model theory and related areas of mathematics, a type is an object that describes how a element or finite collection of elements in a mathematical structure might behave. More precisely, it is a set of first-order formulas in a language L with free variables x1, x2,..., xn that are true of a set of n-tuples of an L-structure . Depending on the context, types can be complete or partial and they may use a fixed set of constants, A, from the structure . The question of which types represent actual elements of leads to the ideas of saturated models and omitting types.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
This is a glossary of set theory.
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations, in the same way that elementary algebra describes numerical operations.
Feferman–Vaught theorem in model theory is a theorem by Solomon Feferman and Robert Lawson Vaught that shows how to reduce, in an algorithmic way, the first-order theory of a product of first-order structures to the first-order theory of elements of the structure.







