Related Research Articles
Systems theory is the transdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or human-made. Every system has causal boundaries, is influenced by its context, defined by its structure, function and role, and expressed through its relations with other systems. A system is "more than the sum of its parts" by expressing synergy or emergent behavior.

Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.
Biophysics is an interdisciplinary science that applies approaches and methods traditionally used in physics to study biological phenomena. Biophysics covers all scales of biological organization, from molecular to organismic and populations. Biophysical research shares significant overlap with biochemistry, molecular biology, physical chemistry, physiology, nanotechnology, bioengineering, computational biology, biomechanics, developmental biology and systems biology.

Biomechanics is the study of the structure, function and motion of the mechanical aspects of biological systems, at any level from whole organisms to organs, cells and cell organelles, using the methods of mechanics. Biomechanics is a branch of biophysics.

Computational biology refers to the use of data analysis, mathematical modeling and computational simulations to understand biological systems and relationships. An intersection of computer science, biology, and big data, the field also has foundations in applied mathematics, chemistry, and genetics. It differs from biological computing, a subfield of computer engineering which uses bioengineering to build computers.
Hemodynamics or haemodynamics are the dynamics of blood flow. The circulatory system is controlled by homeostatic mechanisms of autoregulation, just as hydraulic circuits are controlled by control systems. The hemodynamic response continuously monitors and adjusts to conditions in the body and its environment. Hemodynamics explains the physical laws that govern the flow of blood in the blood vessels.
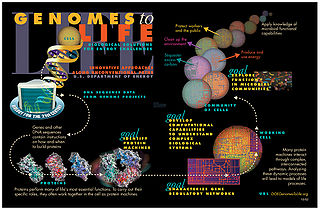
Systems biology is the computational and mathematical analysis and modeling of complex biological systems. It is a biology-based interdisciplinary field of study that focuses on complex interactions within biological systems, using a holistic approach to biological research.
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.
Systems science, also referred to as systems research, or, simply, systems, is a transdisciplinary field concerned with understanding systems—from simple to complex—in nature, society, cognition, engineering, technology and science itself. The field is diverse, spanning the formal, natural, social, and applied sciences.
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of the living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to prove and validate the scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged.

Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.
Computational science, also known as scientific computing, technical computing or scientific computation (SC), is a division of science that uses advanced computing capabilities to understand and solve complex physical problems. This includes
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together. The modern meaning of the term was introduced by Leo Kadanoff in the 1960s, but a simpler version of the concept was already implicit in the van der Waals equation and in the earlier Landau theory of phase transitions, which did not incorporate scaling correctly.

An ecosystem model is an abstract, usually mathematical, representation of an ecological system, which is studied to better understand the real system.
Joshua Morris Epstein is Professor of Epidemiology at the New York University College of Global Public Health. Formerly Professor of Emergency Medicine at Johns Hopkins University, with joint appointments in the departments of Applied Mathematics, Economics, Biostatistics, International Health, and Environmental Health Sciences and the Director of the JHU Center for Advanced Modeling in the Social, Behavioral, and Health Sciences. He is an External Professor at the Santa Fe Institute, a member of the New York Academy of Sciences, and a member of the Institute of Medicine's Committee on Identifying and Prioritizing New Preventive Vaccines.

Carlos Castillo-Chavez is a Mexican-American mathematician who was Regents Professor and Joaquín Bustoz Jr. Professor of Mathematical Biology at Arizona State University. Castillo-Chavez was founder and the Executive Director of the Mathematical and Theoretical Biology Institute (MTBI) and the Institute for Strengthening the Understanding of Mathematics and Science. For 2019, Castillo-Chavez was Provost Visiting Professor in the Applied Mathematics Division and Data Science Initiative at Brown University. Castillo-Chavez retired from Arizona State University at the end of spring 2020.
Nicolas Rashevsky was an American theoretical physicist who was one of the pioneers of mathematical biology, and is also considered the father of mathematical biophysics and theoretical biology.

Artificial life is a field of study wherein researchers examine systems related to natural life, its processes, and its evolution, through the use of simulations with computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American theoretical biologist, in 1986. In 1987 Langton organized the first conference on the field, in Los Alamos, New Mexico. There are three main kinds of alife, named for their approaches: soft, from software; hard, from hardware; and wet, from biochemistry. Artificial life researchers study traditional biology by trying to recreate aspects of biological phenomena.
Cardiophysics is an interdisciplinary science that stands at the junction of cardiology and medical physics, with researchers using the methods of, and theories from, physics to study cardiovascular system at different levels of its organisation, from the molecular scale to whole organisms. Being formed historically as part of systems biology, cardiophysics designed to reveal connections between the physical mechanisms, underlying the organization of the cardiovascular system, and biological features of its functioning.

Abba Gumelpronunciation is a Professor & The Michael and Eugenia Brin Endowed E-Nnovate Chair in Mathematics at the Department of Mathematics, University of Maryland, College Park. His research, which spans three main areas of applied mathematics, is focused on the use of mathematical modeling and rigorous approaches, together with statistical analysis, to gain insight into the dynamics of real-life phenomena arising in the natural and engineering sciences. The main emphasis of Gumel's work is on the mathematical theory of epidemics – specifically, he uses mathematical theories and methodologies to gain insights into the qualitative behavior of nonlinear dynamical systems arising from the mathematical modelling of phenomena in the natural and engineering sciences, with emphasis on the transmission dynamics and control of emerging and re-emerging human infectious diseases of public health and socio-economic interest.