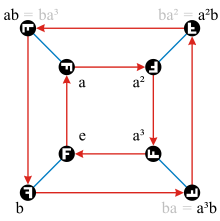
Definition
Let  be a group and
be a group and  be a generating set of
be a generating set of  . The Cayley graph
. The Cayley graph  is an edge-colored directed graph constructed as follows: [2]
is an edge-colored directed graph constructed as follows: [2]
- Each element
 of
of  is assigned a vertex: the vertex set of
is assigned a vertex: the vertex set of  is identified with
is identified with 
- Each element
 of
of  is assigned a color
is assigned a color  .
. - For every
 and
and  , there is a directed edge of color
, there is a directed edge of color  from the vertex corresponding to
from the vertex corresponding to  to the one corresponding to
to the one corresponding to  .
.
Not every convention requires that  generate the group. If
generate the group. If  is not a generating set for
is not a generating set for  , then
, then  is disconnected and each connected component represents a coset of the subgroup generated by
is disconnected and each connected component represents a coset of the subgroup generated by  .
.
If an element  of
of  is its own inverse,
is its own inverse,  then it is typically represented by an undirected edge.
then it is typically represented by an undirected edge.
The set  is often assumed to be finite, especially in geometric group theory, which corresponds to
is often assumed to be finite, especially in geometric group theory, which corresponds to  being locally finite and
being locally finite and  being finitely generated.
being finitely generated.
The set  is sometimes assumed to be symmetric (
is sometimes assumed to be symmetric ( ) and not containing the group identity element. In this case, the uncolored Cayley graph can be represented as a simple undirected graph.
) and not containing the group identity element. In this case, the uncolored Cayley graph can be represented as a simple undirected graph.
Characterization
The group  acts on itself by left multiplication (see Cayley's theorem). This may be viewed as the action of
acts on itself by left multiplication (see Cayley's theorem). This may be viewed as the action of  on its Cayley graph. Explicitly, an element
on its Cayley graph. Explicitly, an element  maps a vertex
maps a vertex  to the vertex
to the vertex  The set of edges of the Cayley graph and their color is preserved by this action: the edge
The set of edges of the Cayley graph and their color is preserved by this action: the edge  is mapped to the edge
is mapped to the edge  , both having color
, both having color  . In fact, all automorphisms of the colored directed graph
. In fact, all automorphisms of the colored directed graph  are of this form, so that
are of this form, so that  is isomorphic to the symmetry group of
is isomorphic to the symmetry group of  . [note 1] [note 2]
. [note 1] [note 2]
The left multiplication action of a group on itself is simply transitive, in particular, Cayley graphs are vertex-transitive. The following is a kind of converse to this:
To recover the group  and the generating set
and the generating set  from the unlabeled directed graph
from the unlabeled directed graph  , select a vertex
, select a vertex  and label it by the identity element of the group. Then label each vertex
and label it by the identity element of the group. Then label each vertex  of
of  by the unique element of
by the unique element of  that maps
that maps  to
to  The set
The set  of generators of
of generators of  that yields
that yields  as the Cayley graph
as the Cayley graph  is the set of labels of out-neighbors of
is the set of labels of out-neighbors of  . Since
. Since  is uncolored, it might have more directed graph automorphisms than the left multiplication maps, for example group automorphisms of
is uncolored, it might have more directed graph automorphisms than the left multiplication maps, for example group automorphisms of  which permute
which permute  .
.
Connection to group theory
Knowledge about the structure of the group can be obtained by studying the adjacency matrix of the graph and in particular applying the theorems of spectral graph theory. Conversely, for symmetric generating sets, the spectral and representation theory of  are directly tied together: take
are directly tied together: take  a complete set of irreducible representations of
a complete set of irreducible representations of  and let
and let  with eigenvalues
with eigenvalues  . Then the set of eigenvalues of
. Then the set of eigenvalues of  is exactly
is exactly  where eigenvalue
where eigenvalue  appears with multiplicity
appears with multiplicity  for each occurrence of
for each occurrence of  as an eigenvalue of
as an eigenvalue of 
The genus of a group is the minimum genus for any Cayley graph of that group. [7]
Geometric group theory
For infinite groups, the coarse geometry of the Cayley graph is fundamental to geometric group theory. For a finitely generated group, this is independent of choice of finite set of generators, hence an intrinsic property of the group. This is only interesting for infinite groups: every finite group is coarsely equivalent to a point (or the trivial group), since one can choose as finite set of generators the entire group.
Formally, for a given choice of generators, one has the word metric (the natural distance on the Cayley graph), which determines a metric space. The coarse equivalence class of this space is an invariant of the group.
Integral classification
An integral graph is one whose eigenvalues are all integers. While the complete classification of integral graphs remains an open problem, the Cayley graphs of certain groups are always integral. Using previous characterizations of the spectrum of Cayley graphs, note that  is integral iff the eigenvalues of
is integral iff the eigenvalues of  are integral for every representation
are integral for every representation  of
of  .
.
Cayley integral simple group
A group  is Cayley integral simple (CIS) if the connected Cayley graph
is Cayley integral simple (CIS) if the connected Cayley graph  is integral exactly when the symmetric generating set
is integral exactly when the symmetric generating set  is the complement of a subgroup of
is the complement of a subgroup of  . A result of Ahmady, Bell, and Mohar shows that all CIS groups are isomorphic to
. A result of Ahmady, Bell, and Mohar shows that all CIS groups are isomorphic to  , or
, or  for primes
for primes  . [9] It is important that
. [9] It is important that  actually generates the entire group
actually generates the entire group  in order for the Cayley graph to be connected. (If
in order for the Cayley graph to be connected. (If  does not generate
does not generate  , the Cayley graph may still be integral, but the complement of
, the Cayley graph may still be integral, but the complement of  is not necessarily a subgroup.)
is not necessarily a subgroup.)
In the example of  , the symmetric generating sets (up to graph isomorphism) are
, the symmetric generating sets (up to graph isomorphism) are
 :
:  is a
is a  -cycle with eigenvalues
-cycle with eigenvalues 
 :
:  is
is  with eigenvalues
with eigenvalues 
The only subgroups of  are the whole group and the trivial group, and the only symmetric generating set
are the whole group and the trivial group, and the only symmetric generating set  that produces an integral graph is the complement of the trivial group. Therefore
that produces an integral graph is the complement of the trivial group. Therefore  must be a CIS group.
must be a CIS group.
The proof of the complete CIS classification uses the fact that every subgroup and homomorphic image of a CIS group is also a CIS group. [9]
Cayley integral group
A slightly different notion is that of a Cayley integral group  , in which every symmetric subset
, in which every symmetric subset  produces an integral graph
produces an integral graph  . Note that
. Note that  no longer has to generate the entire group.
no longer has to generate the entire group.
The complete list of Cayley integral groups is given by  , and the dicyclic group of order
, and the dicyclic group of order  , where
, where  and
and  is the quaternion group. [9] The proof relies on two important properties of Cayley integral groups:
is the quaternion group. [9] The proof relies on two important properties of Cayley integral groups:
- Subgroups and homomorphic images of Cayley integral groups are also Cayley integral groups.
- A group is Cayley integral iff every connected Cayley graph of the group is also integral.
Normal and Eulerian generating sets
Given a general group  , a subset
, a subset  is normal if
is normal if  is closed under conjugation by elements of
is closed under conjugation by elements of  (generalizing the notion of a normal subgroup), and
(generalizing the notion of a normal subgroup), and  is Eulerian if for every
is Eulerian if for every  , the set of elements generating the cyclic group
, the set of elements generating the cyclic group  is also contained in
is also contained in  . A 2019 result by Guo, Lytkina, Mazurov, and Revin proves that the Cayley graph
. A 2019 result by Guo, Lytkina, Mazurov, and Revin proves that the Cayley graph  is integral for any Eulerian normal subset
is integral for any Eulerian normal subset  , using purely representation theoretic techniques. [10]
, using purely representation theoretic techniques. [10]
The proof of this result is relatively short: given  an Eulerian normal subset, select
an Eulerian normal subset, select  pairwise nonconjugate so that
pairwise nonconjugate so that  is the union of the conjugacy classes
is the union of the conjugacy classes  . Then using the characterization of the spectrum of a Cayley graph, one can show the eigenvalues of
. Then using the characterization of the spectrum of a Cayley graph, one can show the eigenvalues of  are given by
are given by  taken over irreducible characters
taken over irreducible characters  of
of  . Each eigenvalue
. Each eigenvalue  in this set must be an element of
in this set must be an element of  for
for  a primitive
a primitive  root of unity (where
root of unity (where  must be divisible by the orders of each
must be divisible by the orders of each  ). Because the eigenvalues are algebraic integers, to show they are integral it suffices to show that they are rational, and it suffices to show
). Because the eigenvalues are algebraic integers, to show they are integral it suffices to show that they are rational, and it suffices to show  is fixed under any automorphism
is fixed under any automorphism  of
of  . There must be some
. There must be some  relatively prime to
relatively prime to  such that
such that  for all
for all  , and because
, and because  is both Eulerian and normal,
is both Eulerian and normal,  for some
for some  . Sending
. Sending  bijects conjugacy classes, so
bijects conjugacy classes, so  and
and  have the same size and
have the same size and  merely permutes terms in the sum for
merely permutes terms in the sum for  . Therefore
. Therefore  is fixed for all automorphisms of
is fixed for all automorphisms of  , so
, so  is rational and thus integral.
is rational and thus integral.
Consequently, if  is the alternating group and
is the alternating group and  is a set of permutations given by
is a set of permutations given by  , then the Cayley graph
, then the Cayley graph  is integral. (This solved a previously open problem from the Kourovka Notebook.) In addition when
is integral. (This solved a previously open problem from the Kourovka Notebook.) In addition when  is the symmetric group and
is the symmetric group and  is either the set of all transpositions or the set of transpositions involving a particular element, the Cayley graph
is either the set of all transpositions or the set of transpositions involving a particular element, the Cayley graph  is also integral.
is also integral.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
In mathematical physics, n-dimensional de Sitter space is a maximally symmetric Lorentzian manifold with constant positive scalar curvature. It is the Lorentzian analogue of an n-sphere.
In statistics, the Wishart distribution is a generalization of the gamma distribution to multiple dimensions. It is named in honor of John Wishart, who first formulated the distribution in 1928. Other names include Wishart ensemble, or Wishart–Laguerre ensemble, or LOE, LUE, LSE.
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by ρ(·).
In mathematics, the Borel–Weil–Bott theorem is a basic result in the representation theory of Lie groups, showing how a family of representations can be obtained from holomorphic sections of certain complex vector bundles, and, more generally, from higher sheaf cohomology groups associated to such bundles. It is built on the earlier Borel–Weil theorem of Armand Borel and André Weil, dealing just with the space of sections, the extension to higher cohomology groups being provided by Raoul Bott. One can equivalently, through Serre's GAGA, view this as a result in complex algebraic geometry in the Zariski topology.

In mathematics, a compact (topological) group is a topological group whose topology realizes it as a compact topological space. Compact groups are a natural generalization of finite groups with the discrete topology and have properties that carry over in significant fashion. Compact groups have a well-understood theory, in relation to group actions and representation theory.
In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, Shinzo Watanabe, I. Shigekawa, and so on finally completed the foundations.
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to quantum chemistry studies of atoms, molecules and solids.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. A WZW model is associated to a Lie group, and its symmetry algebra is the affine Lie algebra built from the corresponding Lie algebra. By extension, the name WZW model is sometimes used for any conformal field theory whose symmetry algebra is an affine Lie algebra.

In mathematics, Burnside's theorem in group theory states that if G is a finite group of order where p and q are prime numbers, and a and b are non-negative integers, then G is solvable. Hence each non-Abelian finite simple group has order divisible by at least three distinct primes.
In mathematical physics, the gamma matrices, also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin particles. Gamma matrices were introduced by Paul Dirac in 1928.
In mathematics, the Harish-Chandra isomorphism, introduced by Harish-Chandra , is an isomorphism of commutative rings constructed in the theory of Lie algebras. The isomorphism maps the center of the universal enveloping algebra of a reductive Lie algebra to the elements of the symmetric algebra of a Cartan subalgebra that are invariant under the Weyl group .
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.

In mathematical physics, the Dirac equation in curved spacetime is a generalization of the Dirac equation from flat spacetime to curved spacetime, a general Lorentzian manifold.
Stochastic portfolio theory (SPT) is a mathematical theory for analyzing stock market structure and portfolio behavior introduced by E. Robert Fernholz in 2002. It is descriptive as opposed to normative, and is consistent with the observed behavior of actual markets. Normative assumptions, which serve as a basis for earlier theories like modern portfolio theory (MPT) and the capital asset pricing model (CAPM), are absent from SPT.
De-sparsified lasso contributes to construct confidence intervals and statistical tests for single or low-dimensional components of a large parameter vector in high-dimensional model.
Batch normalization is a method used to make training of artificial neural networks faster and more stable through normalization of the layers' inputs by re-centering and re-scaling. It was proposed by Sergey Ioffe and Christian Szegedy in 2015.