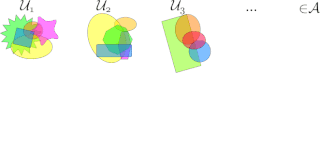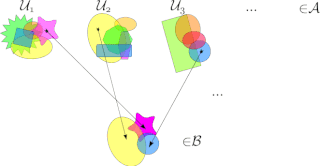Choquet game

Last updated March 30, 2024

The Choquet game is a topological game named after Gustave Choquet, who was in 1969 the first to investigate such games.^[1] A closely related game is known as the strong Choquet game.

Let $X$ be a non-empty topological space. The Choquet game of $X$ , $G(X)$ , is defined as follows: Player I chooses $U_{0}$ , a non-empty open subset of $X$ , then Player II chooses $V_{0}$ , a non-empty open subset of $U_{0}$ , then Player I chooses $U_{1}$ , a non-empty open subset of $V_{0}$ , etc. The players continue this process, constructing a sequence $U_{0}\supseteq V_{0}\supseteq U_{1}\supseteq V_{1}\supseteq U_{2}...$ . If $\bigcap \limits _{i=0}^{\infty }U_{i}=\emptyset$ then Player I wins, otherwise Player II wins.

It was proved by John C. Oxtoby that a non-empty topological space $X$ is a Baire space if and only if Player I has no winning strategy. A nonempty topological space $X$ in which Player II has a winning strategy is called a Choquet space. (Note that it is possible that neither player has a winning strategy.) Thus every Choquet space is Baire. On the other hand, there are Baire spaces (even separable metrizable ones) that are not Choquet spaces, so the converse fails.

The strong Choquet game of $X$ , $G^{s}(X)$ , is defined similarly, except that Player I chooses $(x_{0},U_{0})$ , then Player II chooses $V_{0}$ , then Player I chooses $(x_{1},U_{1})$ , etc, such that $x_{i}\in U_{i},V_{i}$ for all $i$ . A topological space $X$ in which Player II has a winning strategy for $G^{s}(X)$ is called a strong Choquet space. Every strong Choquet space is a Choquet space, although the converse does not hold.

All nonempty complete metric spaces and compact T₂ spaces are strong Choquet. (In the first case, Player II, given $(x_{i},U_{i})$ , chooses $V_{i}$ such that $\operatorname {diam} (V_{i})<1/i$ and $\operatorname {cl} (V_{i})\subseteq V_{i-1}$ . Then the sequence $\left\{x_{i}\right\}\to x\in V_{i}$ for all $i$ .) Any subset of a strong Choquet space that is a $G_{\delta }$ set is strong Choquet. Metrizable spaces are completely metrizable if and only if they are strong Choquet.^[2]^[3]

Related Research Articles

This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations are also continuous functions. Such a topology is called a vector topology and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space. One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Banach spaces, Hilbert spaces and Sobolev spaces are other well-known examples of TVSs.

The Baire category theorem (BCT) is an important result in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space. It is used in the proof of results in many areas of analysis and geometry, including some of the fundamental theorems of functional analysis.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.

In mathematics, a topological space $is said to be a Baire space if countable unions of closed sets with empty interior also have empty interior. According to the Baire category theorem, compact Hausdorff spaces and complete metric spaces are examples of Baire spaces. The Baire category theorem combined with the properties of Baire spaces has numerous applications in topology, geometry, and analysis, in particular functional analysis. For more motivation and applications, see the article Baire category theorem. The current article focuses more on characterizations and basic properties of Baire spaces per se.$

In the mathematical field of general topology, a meagre set is a subset of a topological space that is small or negligible in a precise sense detailed below. A set that is not meagre is called nonmeagre, or of the second category. See below for definitions of other related terms.

In general topology, a branch of mathematics, a non-empty family A of subsets of a set $is said to have the finite intersection property (FIP) if the intersection over any finite subcollection of is non-empty. It has the strong finite intersection property (SFIP) if the intersection over any finite subcollection of is infinite. Sets with the finite intersection property are also called centered systems and filter subbases .$

In general topology, set theory and game theory, a Banach–Mazur game is a topological game played by two players, trying to pin down elements in a set (space). The concept of a Banach–Mazur game is closely related to the concept of Baire spaces. This game was the first infinite positional game of perfect information to be studied. It was introduced by Stanisław Mazur as problem 43 in the Scottish book, and Mazur's questions about it were answered by Banach.

In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish topologists and logicians—Sierpiński, Kuratowski, Tarski and others. However, Polish spaces are mostly studied today because they are the primary setting for descriptive set theory, including the study of Borel equivalence relations. Polish spaces are also a convenient setting for more advanced measure theory, in particular in probability theory.

<span class="mw-page-title-main">Čech cohomology</span>

In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.

In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.

In topology, a branch of mathematics, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deformation retraction is a mapping that captures the idea of continuously shrinking a space into a subspace.

A subset $of a topological space has the property of Baire, or is called an almost open set, if it differs from an open set by a meager set; that is, if there is an open set such that is meager.$

In the mathematical field of topology, a hyperconnected space or irreducible space is a topological space X that cannot be written as the union of two proper closed subsets. The name irreducible space is preferred in algebraic geometry.

In mathematics, a topological game is an infinite game of perfect information played between two players on a topological space. Players choose objects with topological properties such as points, open sets, closed sets and open coverings. Time is generally discrete, but the plays may have transfinite lengths, and extensions to continuum time have been put forth. The conditions for a player to win can involve notions like topological closure and convergence.

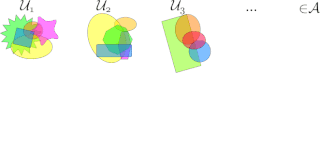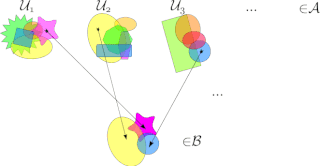
<span class="mw-page-title-main">Selection principle</span> Rule in mathematics

In mathematics, a selection principle is a rule asserting the possibility of obtaining mathematically significant objects by selecting elements from given sequences of sets. The theory of selection principles studies these principles and their relations to other mathematical properties. Selection principles mainly describe covering properties, measure- and category-theoretic properties, and local properties in topological spaces, especially function spaces. Often, the characterization of a mathematical property using a selection principle is a nontrivial task leading to new insights on the characterized property.

In mathematics, a Hurewicz space is a topological space that satisfies a certain basic selection principle that generalizes σ-compactness. A Hurewicz space is a space in which for every sequence of open covers $of the space there are finite sets such that every point of the space belongs to all but finitely many sets .$

In mathematics, a Rothberger space is a topological space that satisfies a certain a basic selection principle. A Rothberger space is a space in which for every sequence of open covers $of the space there are sets such that the family covers the space.$

In mathematics, a $-space$ is a topological space that satisfies a certain a basic selection principle. An infinite cover of a topological space is an $-cover if every finite subset of this space is contained in some member of the cover, and the whole space is not a member the cover. A cover of a topological space is a -cover if every point of this space belongs to all but finitely many members of this cover. A -space is a space in which every open -cover contains a -cover.$

In functional analysis and related areas of mathematics, a metrizable topological vector space (TVS) is a TVS whose topology is induced by a metric. An LM-space is an inductive limit of a sequence of locally convex metrizable TVS.

References

↑ Choquet, Gustave (1969). Lectures on Analysis: Integration and topological vector spaces. W. A. Benjamin. ISBN 9780805369601.
↑ Becker, Howard; Kechris, A. S. (1996). The Descriptive Set Theory of Polish Group Actions. Cambridge University Press. p. 59. ISBN 9780521576055.
↑ Kechris, Alexander (2012). Classical Descriptive Set Theory. Springer Science & Business Media. pp. 43–45. ISBN 9781461241904.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Choquet, Gustave (1969). Lectures on Analysis: Integration and topological vector spaces. W. A. Benjamin. ISBN 9780805369601.

[2] Becker, Howard; Kechris, A. S. (1996). The Descriptive Set Theory of Polish Group Actions. Cambridge University Press. p. 59. ISBN 9780521576055.

[3] Kechris, Alexander (2012). Classical Descriptive Set Theory. Springer Science & Business Media. pp. 43–45. ISBN 9781461241904.

[1]

[2]

[3]