 Convex circular triangle |  Circular horn triangle |
In geometry, a circular triangle is a triangle with circular arc edges.
 Convex circular triangle |  Circular horn triangle |
In geometry, a circular triangle is a triangle with circular arc edges.
 Reuleaux triangle |  Arbelos |
A convex circular triangle may be constructed by three circles intersecting each other and represents the area of intersection. Its edges are all curved outwards. The sum of the internal angles of a circular triangle is greater than 180°. A Reuleaux triangle is a special case based on an equilateral triangle where the center of each arc is on the opposite vertex.
A circular horn triangle is a similar concept, but represents the area interior to 3 mutually tangent circles so all of the internal angles are zero. [1] The arbelos is a special case with three collinear vertices and three semicircular edges. [2]
Other circular triangles can have a mixture of convex and concave circular arc edges.

Long arcs can produce concave figures regardless of whether individual edges are curved inwards or outwards. Inward curved arcs can create self-intersecting forms, such as the a triquetra figure:


Circular triangles can be seen in tessellation.
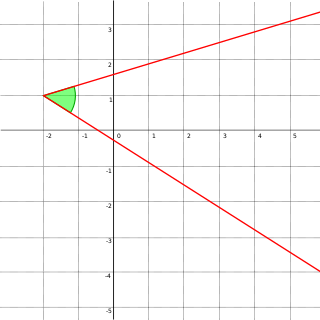
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term oblong is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.
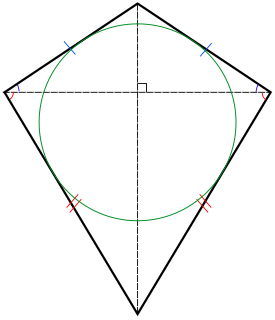
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

A Reuleaux triangle[ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

A simple polygon that is not convex is called concave, non-convex or reentrant. A concave polygon will always have at least one reflex interior angle—that is, an angle with a measure that is between 180 degrees and 360 degrees exclusive.

In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon. Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points.
In geometry, the (angular) defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the Euclidean plane would. The opposite notion is the excess.
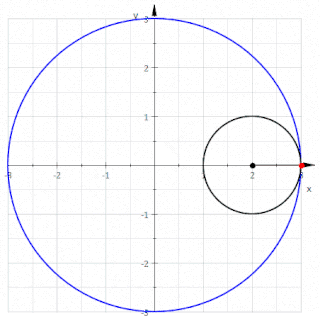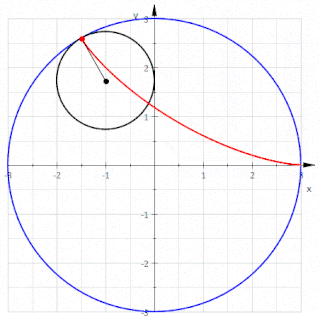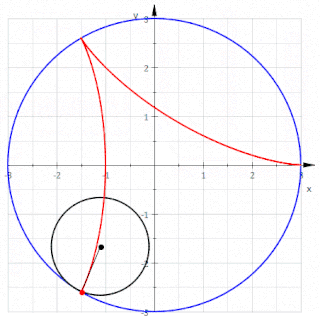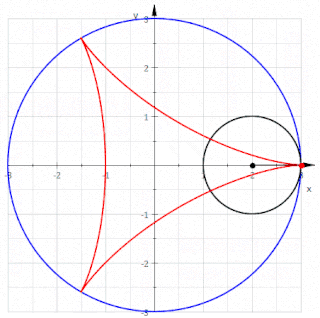
In geometry, a deltoid curve, also known as a tricuspoid curve or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three or one-and-a-half times its radius. It is named after the capital Greek letter delta (Δ) which it resembles.

In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.

In 2-dimensional geometry, a lens is a convex region bounded by two circular arcs joined to each other at their endpoints. In order for this shape to be convex, both arcs must bow outwards (convex-convex). This shape can be formed as the intersection of two circular disks. It can also be formed as the union of two circular segments, joined along a common chord.
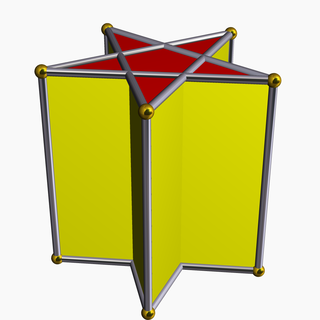
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.
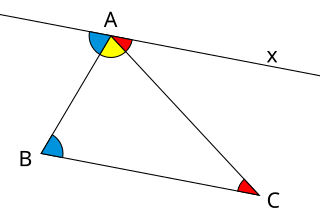
In a Euclidean space, the sum of angles of a triangle equals the straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
In geometry, a vertex, often denoted by letters such as , , , , is a point where two or more curves, lines, or edges meet. As a consequence of this definition, the point where two lines meet to form an angle and the corners of polygons and polyhedra are vertices.

In plane geometry, a lune is the concave-convex region bounded by two circular arcs. It has one boundary portion for which the connecting segment of any two nearby points moves outside the region and another boundary portion for which the connecting segment of any two nearby points lies entirely inside the region. A convex-convex region is termed a lens.

In geometry, the tritetragonal tiling or alternated octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbols of {(4,3,3)} or h{8,3}.