Related Research Articles
In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to plasticity, in which the object fails to do so and instead remains in its deformed state.

In materials science, fatigue is the initiation and propagation of cracks in a material due to cyclic loading. Once a fatigue crack has initiated, it grows a small amount with each loading cycle, typically producing striations on some parts of the fracture surface. The crack will continue to grow until it reaches a critical size, which occurs when the stress intensity factor of the crack exceeds the fracture toughness of the material, producing rapid propagation and typically complete fracture of the structure.

Nacre, also known as mother of pearl, is an organic–inorganic composite material produced by some molluscs as an inner shell layer; it is also the material of which pearls are composed. It is strong, resilient, and iridescent.
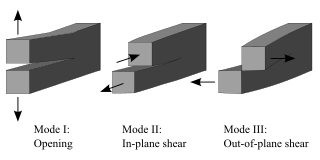
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.

Crazing is the phenomenon that produces a network of fine cracks on the surface of a material, for example in a glaze layer. Crazing frequently precedes fracture in some glassy thermoplastic polymers. As it only takes place under tensile stress, the plane of the crazing corresponds to the stress direction. The effect is visibly distinguishable from other types of fine cracking because the crazing region has different refractive indices from surrounding material. Crazing occurs in regions of high hydrostatic tension, or in regions of very localized yielding, which leads to the formation of interpenetrating microvoids and small fibrils. If an applied tensile load is sufficient, these bridges elongate and break, causing the microvoids to grow and coalesce; as microvoids coalesce, cracks begin to form.

Microstructure is the very small scale structure of a material, defined as the structure of a prepared surface of material as revealed by an optical microscope above 25× magnification. The microstructure of a material can strongly influence physical properties such as strength, toughness, ductility, hardness, corrosion resistance, high/low temperature behaviour or wear resistance. These properties in turn govern the application of these materials in industrial practice.

Stress corrosion cracking (SCC) is the growth of crack formation in a corrosive environment. It can lead to unexpected and sudden failure of normally ductile metal alloys subjected to a tensile stress, especially at elevated temperature. SCC is highly chemically specific in that certain alloys are likely to undergo SCC only when exposed to a small number of chemical environments. The chemical environment that causes SCC for a given alloy is often one which is only mildly corrosive to the metal. Hence, metal parts with severe SCC can appear bright and shiny, while being filled with microscopic cracks. This factor makes it common for SCC to go undetected prior to failure. SCC often progresses rapidly, and is more common among alloys than pure metals. The specific environment is of crucial importance, and only very small concentrations of certain highly active chemicals are needed to produce catastrophic cracking, often leading to devastating and unexpected failure.
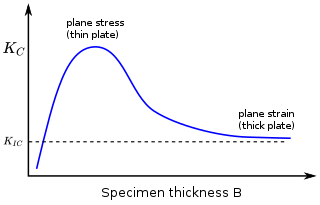
In materials science, fracture toughness is the critical stress intensity factor of a sharp crack where propagation of the crack suddenly becomes rapid and unlimited. A component's thickness affects the constraint conditions at the tip of a crack with thin components having plane stress conditions and thick components having plane strain conditions. Plane strain conditions give the lowest fracture toughness value which is a material property. The critical value of stress intensity factor in mode I loading measured under plane strain conditions is known as the plane strain fracture toughness, denoted . When a test fails to meet the thickness and other test requirements that are in place to ensure plane strain conditions, the fracture toughness value produced is given the designation . Fracture toughness is a quantitative way of expressing a material's resistance to crack propagation and standard values for a given material are generally available.
The J-integral represents a way to calculate the strain energy release rate, or work (energy) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by G. P. Cherepanov and independently in 1968 by James R. Rice, who showed that an energetic contour path integral was independent of the path around a crack.

Embrittlement is a significant decrease of ductility of a material, which makes the material brittle. Embrittlement is used to describe any phenomena where the environment compromises a stressed material's mechanical performance, such as temperature or environmental composition. This is oftentimes undesirable as brittle fracture occurs quicker and can much more easily propagate than ductile fracture, leading to complete failure of the equipment. Various materials have different mechanisms of embrittlement, therefore it can manifest in a variety of ways, from slow crack growth to a reduction of tensile ductility and toughness.

Fractography is the study of the fracture surfaces of materials. Fractographic methods are routinely used to determine the cause of failure in engineering structures, especially in product failure and the practice of forensic engineering or failure analysis. In material science research, fractography is used to develop and evaluate theoretical models of crack growth behavior.
Rubber toughening is a process in which rubber nanoparticles are interspersed within a polymer matrix to increase the mechanical robustness, or toughness, of the material. By "toughening" a polymer it is meant that the ability of the polymeric substance to absorb energy and plastically deform without fracture is increased. Considering the significant advantages in mechanical properties that rubber toughening offers, most major thermoplastics are available in rubber-toughened versions; for many engineering applications, material toughness is a deciding factor in final material selection.
In fracture mechanics, the energy release rate, , is the rate at which energy is transformed as a material undergoes fracture. Mathematically, the energy release rate is expressed as the decrease in total potential energy per increase in fracture surface area, and is thus expressed in terms of energy per unit area. Various energy balances can be constructed relating the energy released during fracture to the energy of the resulting new surface, as well as other dissipative processes such as plasticity and heat generation. The energy release rate is central to the field of fracture mechanics when solving problems and estimating material properties related to fracture and fatigue.
Polymer fracture is the study of the fracture surface of an already failed material to determine the method of crack formation and extension in polymers both fiber reinforced and otherwise. Failure in polymer components can occur at relatively low stress levels, far below the tensile strength because of four major reasons: long term stress or creep rupture, cyclic stresses or fatigue, the presence of structural flaws and stress-cracking agents. Formations of submicroscopic cracks in polymers under load have been studied by x ray scattering techniques and the main regularities of crack formation under different loading conditions have been analyzed. The low strength of polymers compared to theoretically predicted values are mainly due to the many microscopic imperfections found in the material. These defects namely dislocations, crystalline boundaries, amorphous interlayers and block structure can all lead to the non-uniform distribution of mechanical stress.
In materials modeled by linear elastic fracture mechanics (LEFM), crack extension occurs when the applied energy release rate exceeds , where is the material's resistance to crack extension.
Alan G. Thomas (1927-2019) was an international authority on the mechanics of rubbery materials, in particular their fracture mechanics properties. Along with Ronald S. Rivlin, he published the Rupture of Rubber series of articles, beginning in 1953. He was the first to apply Griffith's energy release rate criterion to the analysis of rubber's strength and fatigue behavior.

In mechanical engineering and materials science, a notch refers to a V-shaped, U-shaped, or semi-circular defect deliberately introduced into a planar material. In structural components, a notch causes a stress concentration which can result in the initiation and growth of fatigue cracks. Notches are used in materials characterization to determine fracture mechanics related properties such as fracture toughness and rates of fatigue crack growth.

Microcracks in rock, also known as microfractures and cracks, are spaces in rock with the longest length of 1000 μm and the other two dimensions of 10 μm. In general, the ratio of width to length of microcracks is between 10−3 to 10−5.

Emmanuel E. Gdoutos is a Greek academic, Professor Emeritus at the Democritus University of Thrace and Full Member of the Academy of Athens. He has worked in experimental mechanics, fracture mechanics, composite materials, and sandwich structures. His main scientific accomplishments include the solution of many problems of crack growth under combination of opening-mode and sliding-mode loading which were published in his book: “Problems of Mixed-Mode Crack Propagation." His contributions have been widely recognized worldwide through membership and leadership in scientific societies, national academies and honorary diplomas and awards.
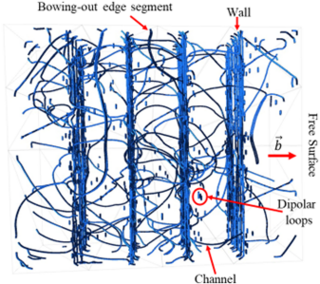
Persistent slip-bands (PSBs) are associated with strain localisation due to fatigue in metals and cracking on the same plane. Transmission electron microscopy (TEM) and three-dimensional discrete dislocation dynamics simulation were used to reveal and understand dislocations type and arrangement/patterns to relate it to the sub-surface structure. PSB – ladder structure – is formed mainly from low-density channels of mobile gliding screw dislocation segments and high-density walls of dipolar edge dislocation segments piled up with tangled bowing-out edge segment and different sizes of dipolar loops scattered between the walls and channels. One type of dislocation loop forms the boundary of a completely enclosed patch of slipped material on the slip plane which terminates at the free surface. Widening of the slip band: Screw dislocation can have high enough resolved shear stress for a glide on more than one slip plane. Cross-slip can occur. But this leaves some segments of dislocation on the original slip plane. Dislocation can cross-slip back on to a parallel primary slip plane. where it forms a new dislocation source, and the process can repeat. These walls in PSBs are a ‘dipole dispersion’ form of stable arrangement of edge dislocations with minimal long-range stress field which has a minimal long-range stress field. Which different to slip-bands that is a planar stack of a stable array that has a strong long-range stress field. And – in the free surface – cut and open (elimination) of dislocation loops at the surface cause the irreversible/persistent surface step associated with slip-bands. Surface relief through extrusion occurs on the Burgers vector direction and extrusion height and PSB depth increase with PSB thickness. PSB and planar walls are parallel and perpendicularly aligned with the normal direction of the Critical resolved shear stress, respectively. And once dislocation saturate and reach its sessile configuration, cracks were observed to nucleate and propagate along PSB extrusions.
References
- ↑ Kienzler, R.; Maugin, G. A. (2002). Configurational mechanics of materials (Vol. 427). Springer.
- ↑ Steinmann, P. (2008). "On boundary potential energies in deformational and configurational mechanics". Journal of the Mechanics and Physics of Solids. 56 (3): 772–800. Bibcode:2008JMPSo..56..772S. doi:10.1016/j.jmps.2007.07.001.
- ↑ Verron, E. (2010). "Configurational mechanics: a tool to investigate fracture and fatigue of rubber" (PDF). Rubber Chemistry and Technology. 83 (3): 270–281. doi:10.5254/1.3525685. S2CID 138329716.