
In mathematics, particularly in complex analysis, a Riemann surface is a one-dimensional complex manifold.
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In the mathematical field of Riemannian geometry, the scalar curvature is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry of the metric near that point. It is defined by a complicated explicit formula in terms of partial derivatives of the metric components, although it is also characterized by the volume of infinitesimally small geodesic balls. In the context of the differential geometry of surfaces, the scalar curvature is twice the Gaussian curvature, and completely characterizes the curvature of a surface. In higher dimensions, however, the scalar curvature only represents one particular part of the Riemann curvature tensor.

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.
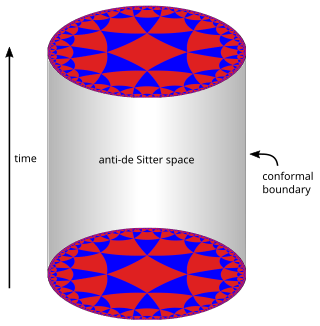
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.

In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane.
In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil. Kähler geometry refers to the study of Kähler manifolds, their geometry and topology, as well as the study of structures and constructions that can be performed on Kähler manifolds, such as the existence of special connections like Hermitian Yang–Mills connections, or special metrics such as Kähler–Einstein metrics.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.

In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman.

In mathematics, a symmetric space is a Riemannian manifold whose group of symmetries contains an inversion symmetry about every point. This can be studied with the tools of Riemannian geometry, leading to consequences in the theory of holonomy; or algebraically through Lie theory, which allowed Cartan to give a complete classification. Symmetric spaces commonly occur in differential geometry, representation theory and harmonic analysis.
In mathematics, an isotropic manifold is a manifold in which the geometry does not depend on directions. Formally, we say that a Riemannian manifold is isotropic if for any point and unit vectors , there is an isometry of with and . Every connected isotropic manifold is homogeneous, i.e. for any there is an isometry of with This can be seen by considering a geodesic :[0,2]\to M} from to and taking the isometry which fixes and maps to
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a complete, finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique. The theorem was proven for closed manifolds by Mostow and extended to finite volume manifolds by Marden (1974) in 3 dimensions, and by Prasad in all dimensions at least 3. Gromov (1981) gave an alternate proof using the Gromov norm. Besson, Courtois & Gallot (1996) gave the simplest available proof.
In differential geometry, the Margulis lemma is a result about discrete subgroups of isometries of a non-positively curved Riemannian manifold. Roughly, it states that within a fixed radius, usually called the Margulis constant, the structure of the orbits of such a group cannot be too complicated. More precisely, within this radius around a point all points in its orbit are in fact in the orbit of a nilpotent subgroup.
In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero. The notion of curvature extends to the category of geodesic metric spaces, where one can use comparison triangles to quantify the curvature of a space; in this context, non-positively curved spaces are known as (locally) CAT(0) spaces.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane : the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value for infinity. With the Riemann model, the point is near to very large numbers, just as the point is near to very small numbers.
In mathematics, hyperbolic complex space is a Hermitian manifold which is the equivalent of the real hyperbolic space in the context of complex manifolds. The complex hyperbolic space is a Kähler manifold, and it is characterised by being the only simply connected Kähler manifold whose holomorphic sectional curvature is constant equal to -1. Its underlying Riemannian manifold has non-constant negative curvature, pinched between -1 and -1/4 : in particular, it is a CAT(-1/4) space.











