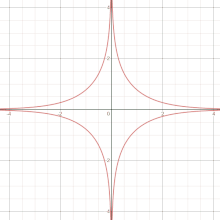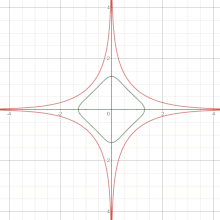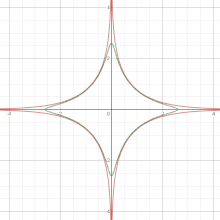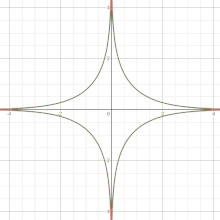
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In mathematics, the Gudermannian function relates a hyperbolic angle measure to a circular angle measure called the gudermannian of and denoted . The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude when parameter

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.

In geometry, a tractrix is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693).

In trigonometry, tangent half-angle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle. The tangent of half an angle is the stereographic projection of the circle through the point at angle radians onto the line through the angles . Among these formulas are the following:

In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of xy = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.
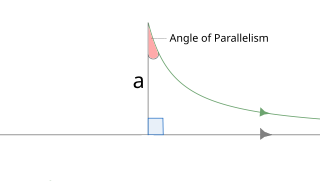
In hyperbolic geometry, angle of parallelism is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
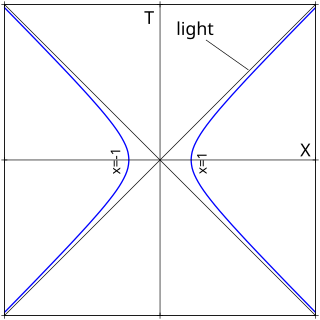
Hyperbolic motion is the motion of an object with constant proper acceleration in special relativity. It is called hyperbolic motion because the equation describing the path of the object through spacetime is a hyperbola, as can be seen when graphed on a Minkowski diagram whose coordinates represent a suitable inertial (non-accelerated) frame. This motion has several interesting features, among them that it is possible to outrun a photon if given a sufficient head start, as may be concluded from the diagram.
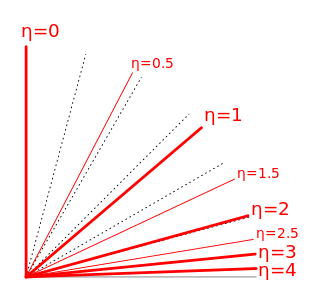
In experimental particle physics, pseudorapidity, , is a commonly used spatial coordinate describing the angle of a particle relative to the beam axis. It is defined as

In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with arc- or ar-.

Rapidity is a measure for relativistic velocity. For one-dimensional motion, rapidities are additive. However, velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are almost exactly proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of n-dimensional hyperbolic geometry in which points are represented by points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space or by the displacement vectors from the origin to those points, and m-planes are represented by the intersections of (m+1)-planes passing through the origin in Minkowski space with S+ or by wedge products of m vectors. Hyperbolic space is embedded isometrically in Minkowski space; that is, the hyperbolic distance function is inherited from Minkowski space, analogous to the way spherical distance is inherited from Euclidean distance when the n-sphere is embedded in (n+1)-dimensional Euclidean space.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
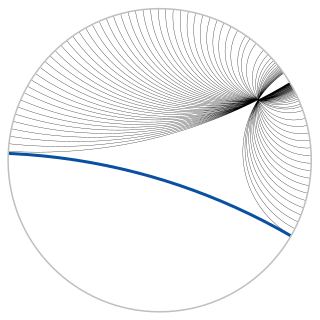
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.

In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities,