Cosmic age problem

Last updated

The cosmic age problem was a historical problem in astronomy concerning the age of the universe. The problem was that at various times in the 20th century, the universe was estimated to be younger than the oldest observed stars. Estimates of the universe's age came from measurements of the current expansion rate of the universe, the Hubble constant , as well as cosmological models relating to the universe's matter and energy contents (see the Friedmann equations). Issues with measuring as well as not knowing about the existence of dark energy led to spurious estimates of the age. [1] [2] Additionally, objects such as galaxies, stars, and planets could not have existed in the extreme temperatures and densities shortly after the Big Bang.

Contents

Since around 1997–2003, the problem is believed to have been solved by most cosmologists: modern cosmological measurements lead to a precise estimate of the age of the universe (i.e. time since the Big Bang) of 13.8 billion years, and recent age estimates for the oldest objects are either younger than this, or consistent allowing for measurement uncertainties.

Historical development

Early years

Following theoretical developments of the Friedmann equations by Alexander Friedmann and Georges Lemaître in the 1920s, and the discovery of the expanding universe by Edwin Hubble in 1929, it was immediately clear that tracing this expansion backwards in time predicts that the universe had almost zero size at a finite time in the past. This concept, initially known as the "Primeval Atom" by Lemaitre, was later elaborated into the modern Big Bang theory. If the universe had expanded at a constant rate in the past, the age of the universe now (i.e. the time since the Big Bang) is simply proportional to the inverse of the Hubble constant, often known as the Hubble time. For Big Bang models with zero cosmological constant and positive matter density, the actual age must be somewhat younger than this Hubble time; typically the age would be between 66% and 90% of the Hubble time[ citation needed ], depending on the density of matter.

Hubble's early estimate of his constant [3] was 550 (km/s)/Mpc, and the inverse of that is 1.8 billion years. It was believed by many geologists such as Arthur Holmes in the 1920s that the Earth was probably over 2 billion years old, but with large uncertainty.[ citation needed ] The possible discrepancy between the ages of the Earth and the universe was probably one motivation for the development of the Steady State theory in 1948 as an alternative to the Big Bang; [4] in the (now obsolete) steady state theory, the universe is infinitely old and on average unchanging with time. The steady state theory postulated spontaneous creation of matter to keep the average density constant as the universe expands, and therefore most galaxies still have an age less than 1/H0. However, if H0 had been 550 (km/s)/Mpc, our Milky Way galaxy would be exceptionally large compared to most other galaxies, so it could well be much older than an average galaxy, therefore eliminating the age problem.

1950–1970

In the 1950s, two substantial errors were discovered in Hubble's extragalactic distance scale: first in 1952, Walter Baade discovered there were two classes of Cepheid variable star. Hubble's sample comprised different classes nearby and in other galaxies, and correcting this error made all other galaxies twice as distant as Hubble's values, thus doubling the Hubble time. [5] A second error was discovered by Allan Sandage and coworkers: for galaxies beyond the Local Group, Cepheids were too faint to observe with Hubble's instruments, so Hubble used the brightest stars as distance indicators. Many of Hubble's "brightest stars" were actually HII regions or clusters containing many stars, which caused another underestimation of distances for these more distant galaxies. [6] Thus, in 1958 Sandage [7] published the first reasonably accurate measurement of the Hubble constant, at 75 (km/s)/Mpc, which is close to modern estimates of 68–74 (km/s)/Mpc. [8]

The age of the Earth (actually the Solar System) was first accurately measured around 1955 by Clair Patterson at 4.55 billion years, [9] essentially identical to the modern value. For H0 ~ 75 (km/s)/Mpc, the inverse of H0 is 13.0 billion years; so after 1958 the Big Bang model age was comfortably older than the Earth.

However, in the 1960s and onwards, new developments in the theory of stellar evolution enabled age estimates for large star clusters called globular clusters: these generally gave age estimates of around 15 billion years, with substantial scatter.[ citation needed ] Further revisions of the Hubble constant by Sandage and Gustav Tammann in the 1970s gave values around 50–60 (km/s)/Mpc, [10] and an inverse of 16-20 billion years, consistent with globular cluster ages.

1975–1990

However, in the late 1970s to early 1990s, the age problem re-appeared: new estimates of the Hubble constant gave higher values, with Gerard de Vaucouleurs estimating values 90–100 (km/s)/Mpc, [11] while Marc Aaronson and co-workers gave values around 80-90  (km/s)/Mpc. [12] Sandage and Tammann continued to argue for values 50–60, leading to a period of controversy sometimes called the "Hubble wars".[ citation needed ] The higher values for H0 appeared to predict a universe younger than the globular cluster ages, and gave rise to some speculations during the 1980s that the Big Bang model was seriously incorrect.

Late 1990s: probable solution

The age problem was eventually thought to be resolved by several developments between 1995 and 2003: firstly, a large program with the Hubble Space Telescope measured the Hubble constant at 72 (km/s)/Mpc with 10 percent uncertainty. [13] Secondly, measurements of parallax by the Hipparcos spacecraft in 1995 revised globular cluster distances upwards by 5-10 percent; [14] this made their stars brighter than previously estimated and therefore younger, shifting their age estimates down to around 12-13 billion years. [15] Finally, from 1998 to 2003 a number of new cosmological observations including supernovae, cosmic microwave background observations and large galaxy redshift surveys led to the acceptance of dark energy and the establishment of the Lambda-CDM model as the standard model of cosmology. The presence of dark energy implies that the universe was expanding more slowly at around half its present age than today, which makes the universe older for a given value of the Hubble constant. The combination of the three results above essentially removed the discrepancy between estimated globular cluster ages and the age of the universe. [16]

More recent measurements from WMAP and the Planck spacecraft lead to an estimate of the age of the universe of 13.80 billion years [17] with only 0.3 percent uncertainty (based on the standard Lambda-CDM model), and modern age measurements for globular clusters [18] and other objects are currently smaller than this value (within the measurement uncertainties). A substantial majority of cosmologists therefore believe the age problem is now resolved. [19]

New research from teams, including one led by Nobel laureate Adam Riess of the Space Telescope Science Institute in Baltimore, has found the universe to be between 12.5 and 13 billion years old, disagreeing with the Planck findings. Whether this stems merely from errors in data gathering, or is related to the as yet unexplained aspects of physics, such as Dark Energy or Dark Matter, has yet to be confirmed. [20]

Dynamical modeling of the universe

In this section, we wish to explore the effect of the dynamical modeling of the universe on the estimate of the universe's age. We will assume the modern observed Hubble value km/s/Mpc so that the discussion below focuses on the effect of the dynamical modeling and less on the effect of the historical accuracy of the Hubble constant.

The 1932 Einstein-de Sitter model of the universe assumes that the universe is filled with only matter and has vanishing curvature. This model received some popularity in the 1980s and offers an explicit solution for the scale factor (see, e.g., D. Baumann 2022) [2]

where is the universe's current age. This then implies that the age of the universe is directly related to the Hubble constant

Substituting in the Hubble constant, the universe has an age of billion years, in disagreement with, e.g., the age of the oldest stars.

If one then allows for dark energy in the form of a cosmological constant in addition to matter, this two-component model predicts the following relationship between age and the Hubble constant

Plugging in observed values of the density parameters results in an age of the universe billion years, now consistent with stellar age observations.

Related Research Articles

<span class="mw-page-title-main">Big Bang</span> Physical theory describing the expansion of the universe

The Big Bang is a physical theory that describes how the universe expanded from an initial state of high density and temperature. The Big Bang theory was inspired by the discovery of the expanding Universe by Edwin Hubble. It was first proposed in 1927 by Roman Catholic priest and physicist Georges Lemaître. Lemaître reasoned that if we go back in time, there must be fewer and fewer matter, until all the energy of the universe is packed in a unique quantum. Various cosmological models of the Big Bang explain the evolution of the observable universe from the earliest known periods through its subsequent large-scale form. These models offer a comprehensive explanation for a broad range of observed phenomena, including the abundance of light elements, the cosmic microwave background (CMB) radiation, and large-scale structure. The overall uniformity of the universe, known as the flatness problem, is explained through cosmic inflation: a sudden and very rapid expansion of space during the earliest moments. However, physics currently lacks a widely accepted theory of quantum gravity that can successfully model the earliest conditions of the Big Bang.

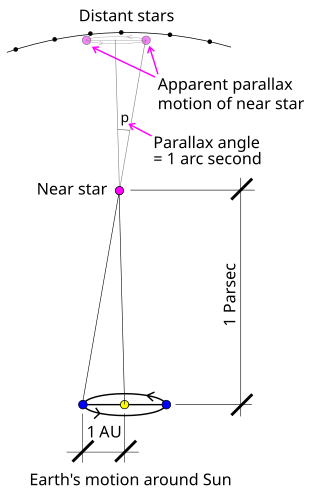
<span class="mw-page-title-main">Parsec</span> Unit of length used in astronomy

The parsec is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (AU), i.e. 30.9 trillion kilometres. The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 AU subtends an angle of one arcsecond. The nearest star, Proxima Centauri, is about 1.3 parsecs from the Sun: from that distance, the gap between the Earth and the Sun spans slightly less than 1/3600 of one degree of view. Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand parsecs, and the Andromeda Galaxy at over 700,000 parsecs.

<span class="mw-page-title-main">Redshift</span> Change of wavelength in photons during travel

In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation. The opposite change, a decrease in wavelength and increase in frequency and energy, is known as a blueshift, or negative redshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. The main causes of electromagnetic redshift in astronomy and cosmology are the relative motions of radiation sources, which give rise to the relativistic Doppler effect, and gravitational potentials, which gravitationally redshift escaping radiation. All sufficiently distant light sources show cosmological redshift corresponding to recession speeds proportional to their distances from Earth, a fact known as Hubble's law that implies the universe is expanding.

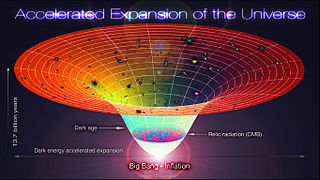
<span class="mw-page-title-main">Accelerating expansion of the universe</span> Cosmological phenomenon

Observations show that the expansion of the universe is accelerating, such that the velocity at which a distant galaxy recedes from the observer is continuously increasing with time. The accelerated expansion of the universe was discovered in 1998 by two independent projects, the Supernova Cosmology Project and the High-Z Supernova Search Team, which used distant type Ia supernovae to measure the acceleration. The idea was that as type Ia supernovae have almost the same intrinsic brightness, and since objects that are farther away appear dimmer, the observed brightness of these supernovae can be used to measure the distance to them. The distance can then be compared to the supernovae's cosmological redshift, which measures how much the universe has expanded since the supernova occurred; the Hubble law established that the farther away that an object is, the faster it is receding. The unexpected result was that objects in the universe are moving away from one another at an accelerating rate. Cosmologists at the time expected that recession velocity would always be decelerating, due to the gravitational attraction of the matter in the universe. Three members of these two groups have subsequently been awarded Nobel Prizes for their discovery. Confirmatory evidence has been found in baryon acoustic oscillations, and in analyses of the clustering of galaxies.

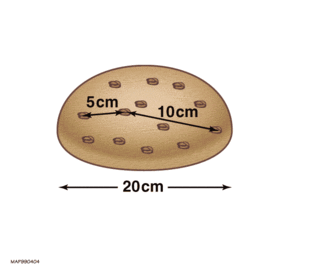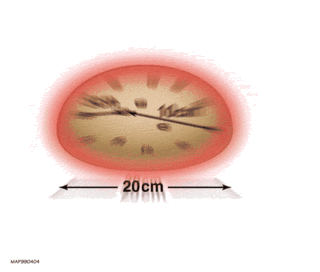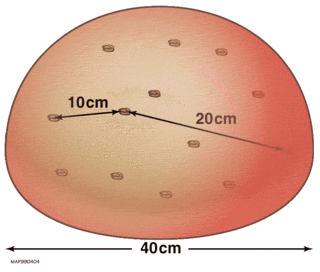
<span class="mw-page-title-main">Hubble's law</span> Observation in physical cosmology

Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving away from Earth. The velocity of the galaxies has been determined by their redshift, a shift of the light they emit toward the red end of the visible spectrum. The discovery of Hubble's law is attributed to Edwin Hubble's work published in 1929.

In physical cosmology, the Big Rip is a hypothetical cosmological model concerning the ultimate fate of the universe, in which the matter of the universe, from stars and galaxies to atoms and subatomic particles, and even spacetime itself, is progressively torn apart by the expansion of the universe at a certain time in the future, until distances between particles will infinitely increase. According to the standard model of cosmology, the scale factor of the universe is accelerating, and, in the future era of cosmological constant dominance, will increase exponentially. However, this expansion is similar for every moment of time, and is characterized by an unchanging, small Hubble constant, effectively ignored by any bound material structures. By contrast, in the Big Rip scenario the Hubble constant increases to infinity in a finite time.

<span class="mw-page-title-main">Observable universe</span> All of space observable from the Earth at the present

The observable universe is a ball-shaped region of the universe comprising all matter that can be observed from Earth or its space-based telescopes and exploratory probes at the present time; the electromagnetic radiation from these objects has had time to reach the Solar System and Earth since the beginning of the cosmological expansion. Initially, it was estimated that there may be 2 trillion galaxies in the observable universe. That number was reduced in 2021 to only several hundred billion based on data from New Horizons. Assuming the universe is isotropic, the distance to the edge of the observable universe is roughly the same in every direction. That is, the observable universe is a spherical region centered on the observer. Every location in the universe has its own observable universe, which may or may not overlap with the one centered on Earth.

<span class="mw-page-title-main">Cosmic distance ladder</span> Succession of methods by which astronomers determine the distances to celestial objects

The cosmic distance ladder is the succession of methods by which astronomers determine the distances to celestial objects. A direct distance measurement of an astronomical object is possible only for those objects that are "close enough" to Earth. The techniques for determining distances to more distant objects are all based on various measured correlations between methods that work at close distances and methods that work at larger distances. Several methods rely on a standard candle, which is an astronomical object that has a known luminosity.

<span class="mw-page-title-main">Allan Sandage</span> American astronomer

Allan Rex Sandage was an American astronomer. He was Staff Member Emeritus with the Carnegie Observatories in Pasadena, California. He determined the first reasonably accurate values for the Hubble constant and the age of the universe.

In physical cosmology, the age of the universe is the time elapsed since the Big Bang. Astronomers have derived two different measurements of the age of the universe: a measurement based on direct observations of an early state of the universe, which indicate an age of 13.787±0.020 billion years as interpreted with the Lambda-CDM concordance model as of 2021; and a measurement based on the observations of the local, modern universe, which suggest a younger age. The uncertainty of the first kind of measurement has been narrowed down to 20 million years, based on a number of studies that all show similar figures for the age. These studies include researches of the microwave background radiation by the Planck spacecraft, the Wilkinson Microwave Anisotropy Probe and other space probes. Measurements of the cosmic background radiation give the cooling time of the universe since the Big Bang, and measurements of the expansion rate of the universe can be used to calculate its approximate age by extrapolating backwards in time. The range of the estimate is also within the range of the estimate for the oldest observed star in the universe.

Tired light is a class of hypothetical redshift mechanisms that was proposed as an alternative explanation for the redshift-distance relationship. These models have been proposed as alternatives to the models that involve the expansion of the universe. The concept was first proposed in 1929 by Fritz Zwicky, who suggested that if photons lost energy over time through collisions with other particles in a regular way, the more distant objects would appear redder than more nearby ones.

The expansion of the universe is parametrized by a dimensionless scale factor. Also known as the cosmic scale factor or sometimes the Robertson Walker scale factor, this is a key parameter of the Friedmann equations.

<span class="mw-page-title-main">Messier 90</span> Galaxy in the constellation Virgo

Messier 90 is an intermediate spiral galaxy exhibiting a weak inner ring structure about 60 million light-years away in the constellation Virgo. It was discovered by Charles Messier in 1781.

The Lambda-CDM, Lambda cold dark matter, or ΛCDM model is a mathematical model of the Big Bang theory with three major components:

  1. a cosmological constant denoted by lambda (Λ) associated with dark energy
  2. the postulated cold dark matter
  3. ordinary matter
<span class="mw-page-title-main">IC 1101</span> Galaxy in the constellation Virgo

IC 1101 is a class S0 supergiant (cD) lenticular galaxy at the center of the Abell 2029 galaxy cluster. It has an isophotal diameter at about 123.65 to 169.61 kiloparsecs. It possesses a diffuse core which is the largest known core of any galaxy to date, and contains a supermassive black hole, one of the largest discovered. The galaxy is located at 354.0 megaparsecs from Earth. The galaxy was discovered on 19 June 1790, by the British astronomer William Herschel.

The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion; the universe does not expand "into" anything and does not require space to exist "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation only applies with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.

Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly observable, but is more convenient for calculations. The distance measures discussed here all reduce to the common notion of Euclidean distance at low redshift.

In cosmology, baryon acoustic oscillations (BAO) are fluctuations in the density of the visible baryonic matter of the universe, caused by acoustic density waves in the primordial plasma of the early universe. In the same way that supernovae provide a "standard candle" for astronomical observations, BAO matter clustering provides a "standard ruler" for length scale in cosmology. The length of this standard ruler is given by the maximum distance the acoustic waves could travel in the primordial plasma before the plasma cooled to the point where it became neutral atoms, which stopped the expansion of the plasma density waves, "freezing" them into place. The length of this standard ruler can be measured by looking at the large scale structure of matter using astronomical surveys. BAO measurements help cosmologists understand more about the nature of dark energy by constraining cosmological parameters.

<span class="mw-page-title-main">Steady-state model</span> Model of the universe – alternative to the Big Bang model

In cosmology, the steady-state model or steady state theory is an alternative to the Big Bang theory. In the steady-state model, the density of matter in the expanding universe remains unchanged due to a continuous creation of matter, thus adhering to the perfect cosmological principle, a principle that says that the observable universe is always the same at any time and any place.

<span class="mw-page-title-main">SN Refsdal</span> Supernova that has been lensed

SN Refsdal is the first detected multiply-lensed supernova, visible within the field of the galaxy cluster MACS J1149+2223. It was named after Norwegian astrophysicist Sjur Refsdal, who, in 1964, first proposed using time-delayed images from a lensed supernova to study the expansion of the universe. The observations were made using the Hubble Space Telescope.

References

  1. ↑ Evidence for the Big Bang by Björn Feuerbacher and Ryan Scranton. January 25, 2006. Retrieved 16 April 2007.
  2. 1 2 Baumann, Daniel (2022). Cosmology. Cambridge University Press. doi:10.1017/9781108937092. ISBN   9781108838078.
  3. ↑ Hubble, E. (15 March 1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi: 10.1073/pnas.15.3.168 . PMC   522427 . PMID   16577160.
  4. ↑ Kragh, Helge (1999). Cosmology and Controversy . Princeton Univ. Press. ISBN   978-0691005461.
  5. ↑ Baade, W. (February 1956). "The Period-Luminosity Relation of the Cepheids". Publications of the Astronomical Society of the Pacific. 68 (400): 5. Bibcode:1956PASP...68....5B. doi: 10.1086/126870 .
  6. ↑ Humason, M. L.; Mayall, N. U.; Sandage, A. R. (April 1956). "Redshifts and magnitudes of extragalactic nebulae". The Astronomical Journal. 61: 97. Bibcode:1956AJ.....61...97H. doi:10.1086/107297.
  7. ↑ Sandage, Allan (1958). "Current Problems in the Extragalactic Distance Scale". Astrophysical Journal. 127: 513. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
  8. ↑ Riess, A.; Macri, Lucas; Casertano, Stefano; Lampeitl, Hubert; Ferguson, Henry C.; Filippenko, Alexei V.; Jha, Saurabh W.; Li, Weidong; Chornock, Ryan (2011). "A 3% solution: determination of the Hubble constant with the Hubble Space Telescope". Astrophysical Journal. 730 (119): 119. arXiv: 1103.2976 . Bibcode:2011ApJ...730..119R. doi:10.1088/0004-637X/730/2/119. S2CID   53531339.
  9. ↑ Patterson, C.; Tilton, G.; Inghram, M. (21 January 1955). "Age of the Earth". Science. 121 (3134): 69–75. Bibcode:1955Sci...121...69P. doi:10.1126/science.121.3134.69. PMID   17782556.
  10. ↑ Sandage, A.; Tammann, G. A. (1976). "Steps toward the Hubble constant. VII - Distances to NGC 2403, M101, and the Virgo cluster using 21 centimeter line widths compared with optical methods: The global value of H sub 0". The Astrophysical Journal. 210: 7. Bibcode:1976ApJ...210....7S. doi: 10.1086/154798 .
  11. ↑ de Vaucouleurs, G. (23 September 1982). "Five crucial tests of the cosmic distance scale using the Galaxy as fundamental standard". Nature. 299 (5881): 303–307. Bibcode:1982Natur.299..303D. doi:10.1038/299303a0. S2CID   4331115.
  12. ↑ Aaronson, M.; Bothun, G.; Mould, J.; Huchra, J.; Schommer, R. A.; Cornell, M. E. (1986). "A distance scale from the infrared magnitude/H I velocity-width relations. V - Distance moduli to 10 galaxy clusters, and positive detection of bulk supercluster motion toward the microwave anisotropy". The Astrophysical Journal. 302: 536. Bibcode:1986ApJ...302..536A. doi:10.1086/164014.
  13. ↑ Madore, Barry F.; Freedman, Wendy L.; Silbermann, N.; Harding, Paul; Huchra, John; Mould, Jeremy R.; Graham, John A.; Ferrarese, Laura; Gibson, Brad K.; Han, Mingsheng; Hoessel, John G.; Hughes, Shaun M.; Illingworth, Garth D.; Phelps, Randy; Sakai, Shoko; Stetson, Peter (10 April 1999). "The Key Project on the Extragalactic Distance Scale. XV. A Cepheid Distance to the Fornax Cluster and Its Implications". The Astrophysical Journal. 515 (1): 29–41. arXiv: astro-ph/9812157 . Bibcode:1999ApJ...515...29M. doi:10.1086/307004. S2CID   119389510.
  14. ↑ Reid, N (1998). "Globular clusters, Hipparcos, and the age of the galaxy". Proceedings of the National Academy of Sciences of the United States of America. 95 (1): 8–12. Bibcode:1998PNAS...95....8R. doi: 10.1073/pnas.95.1.8 . PMC   34182 . PMID   9419316.
  15. ↑ Chaboyer, Brian; Demarque, P.; Kernan, Peter J.; Krauss, Lawrence M. (10 February 1998). "The Age of Globular Clusters in Light of : Resolving the Age Problem?". The Astrophysical Journal. 494 (1): 96–110. arXiv: astro-ph/9706128 . Bibcode:1998ApJ...494...96C. doi:10.1086/305201. S2CID   14638994.
  16. ↑ Krauss, Lawrence M.; Chaboyer, Brian (3 January 2003). "Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology". Science. 299 (5603): 65–69. Bibcode:2003Sci...299...65K. doi:10.1126/science.1075631. PMID   12511641. S2CID   10814581.
  17. ↑ Planck Collaboration, Planck; Ade, P. A. R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A. J.; Barreiro, R. B.; Bartlett, J. G.; Battaner, E.; Benabed, K.; Benoît, A.; Benoit-Lévy, A.; Bernard, J. -P.; Bersanelli, M.; Bielewicz, P.; Bobin, J.; Bock, J. J.; Bonaldi, A.; Bond, J. R.; Borrill, J.; Bouchet, F. R.; Bridges, M.; Bucher, M.; Burigana, C.; Butler, R. C.; et al. (2013). "Planck 2013 results XVI: Cosmological Parameters". Astronomy. 571: A16. arXiv: 1303.5076 . Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID   118349591.
  18. ↑ VandenBerg, Don A.; Brogaard, K.; Leaman, R.; Casagrande, L. (1 October 2013). "The Ages of 55 Globular Clusters as Determined Using an Improved ΔVHB
    TO     Method Along with Color-Magnitude Diagram Constraints, and Their Implications for Broader Issues". The Astrophysical Journal. 775 (2): 134. arXiv: 1308.2257 . Bibcode:2013ApJ...775..134V. doi:10.1088/0004-637X/775/2/134. S2CID   117065283.
  19. ↑ "Cosmological Parameters" (PDF). Review of Particle Properties 2014. Particle Data Group.
  20. ↑ "The universe may be a billion years younger than we thought". NBCNews.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.