Counterexample

Last updated June 09, 2024

A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy.^[1] For example, the fact that "student John Smith is not lazy" is a counterexample to the generalization "students are lazy", and both a counterexample to, and disproof of, the universal quantification "all students are lazy."^[2]

In mathematics

In mathematics, counterexamples are often used to prove the boundaries of possible theorems. By using counterexamples to show that certain conjectures are false, mathematical researchers can then avoid going down blind alleys and learn to modify conjectures to produce provable theorems. It is sometimes said that mathematical development consists primarily in finding (and proving) theorems and counterexamples.^[3]

Rectangle example

Suppose that a mathematician is studying geometry and shapes, and she wishes to prove certain theorems about them. She conjectures that "All rectangles are squares", and she is interested in knowing whether this statement is true or false.

In this case, she can either attempt to prove the truth of the statement using deductive reasoning, or she can attempt to find a counterexample of the statement if she suspects it to be false. In the latter case, a counterexample would be a rectangle that is not a square, such as a rectangle with two sides of length 5 and two sides of length 7. However, despite having found rectangles that were not squares, all the rectangles she did find had four sides. She then makes the new conjecture "All rectangles have four sides". This is logically weaker than her original conjecture, since every square has four sides, but not every four-sided shape is a square.

The above example explained — in a simplified way — how a mathematician might weaken her conjecture in the face of counterexamples, but counterexamples can also be used to demonstrate the necessity of certain assumptions and hypothesis. For example, suppose that after a while, the mathematician above settled on the new conjecture "All shapes that are rectangles and have four sides of equal length are squares". This conjecture has two parts to the hypothesis: the shape must be 'a rectangle' and must have 'four sides of equal length'. The mathematician then would like to know if she can remove either assumption, and still maintain the truth of her conjecture. This means that she needs to check the truth of the following two statements:

"All shapes that are rectangles are squares."
"All shapes that have four sides of equal length are squares".

A counterexample to (1) was already given above, and a counterexample to (2) is a non-square rhombus. Thus, the mathematician now knows that each assumption by itself is insufficient.

Other mathematical examples

A counterexample to the statement "all prime numbers are odd numbers" is the number 2, as it is a prime number but is not an odd number.^[1] Neither of the numbers 7 or 10 is a counterexample, as neither of them are enough to contradict the statement. In this example, 2 is in fact the only possible counterexample to the statement, even though that alone is enough to contradict the statement. In a similar manner, the statement "All natural numbers are either prime or composite" has the number 1 as a counterexample, as 1 is neither prime nor composite.

Euler's sum of powers conjecture was disproved by counterexample. It asserted that at least nn^th powers were necessary to sum to another n^th power. This conjecture was disproved in 1966,^[4] with a counterexample involving n = 5; other n = 5 counterexamples are now known, as well as some n = 4 counterexamples.^[5]

Witsenhausen's counterexample shows that it is not always true (for control problems) that a quadratic loss function and a linear equation of evolution of the state variable imply optimal control laws that are linear.

All Euclidean plane isometries are mappings that preserve area, but the converse is false as shown by counterexamples shear mapping and squeeze mapping.

Other examples include the disproofs of the Seifert conjecture, the Pólya conjecture, the conjecture of Hilbert's fourteenth problem, Tait's conjecture, and the Ganea conjecture.

In philosophy

In philosophy, counterexamples are usually used to argue that a certain philosophical position is wrong by showing that it does not apply in certain cases. Alternatively, the first philosopher can modify their claim so that the counterexample no longer applies; this is analogous to when a mathematician modifies a conjecture because of a counterexample.

For example, in Plato's Gorgias , Callicles, trying to define what it means to say that some people are "better" than others, claims that those who are stronger are better.

But Socrates replies that, because of their strength of numbers, the class of common rabble is stronger than the propertied class of nobles, even though the masses are prima facie of worse character. Thus Socrates has proposed a counterexample to Callicles' claim, by looking in an area that Callicles perhaps did not expect — groups of people rather than individual persons.

Callicles might challenge Socrates' counterexample, arguing perhaps that the common rabble really are better than the nobles, or that even in their large numbers, they still are not stronger. But if Callicles accepts the counterexample, then he must either withdraw his claim, or modify it so that the counterexample no longer applies. For example, he might modify his claim to refer only to individual persons, requiring him to think of the common people as a collection of individuals rather than as a mob.

As it happens, he modifies his claim to say "wiser" instead of "stronger", arguing that no amount of numerical superiority can make people wiser.

Related Research Articles

<span class="mw-page-title-main">Conjecture</span> Proposition in mathematics that is unproven

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.

In the mathematical field of geometric topology, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.

In mathematics, a theorem is a statement that has been proved, or can be proved. The proof of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems.

A mathematical proof is a deductive argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.

In mathematics, the adjective trivial is often used to refer to a claim or a case which can be readily obtained from context, or an object which possesses a simple structure. The noun triviality usually refers to a simple technical aspect of some proof or definition. The origin of the term in mathematical language comes from the medieval trivium curriculum, which distinguishes from the more difficult quadrivium curriculum. The opposite of trivial is nontrivial, which is commonly used to indicate that an example or a solution is not simple, or that a statement or a theorem is not easy to prove.

In mathematics, the Hodge conjecture is a major unsolved problem in algebraic geometry and complex geometry that relates the algebraic topology of a non-singular complex algebraic variety to its subvarieties.

In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof, which proves the existence of a particular kind of object without providing an example. For avoiding confusion with the stronger concept that follows, such a constructive proof is sometimes called an effective proof.

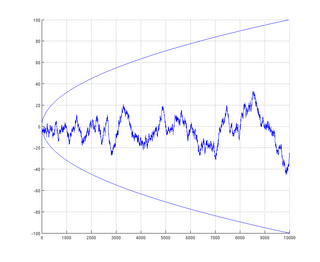
In mathematics, the Mertens conjecture is the statement that the Mertens function $is bounded by . Although now disproven, it had been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens, and disproved by Andrew Odlyzko and Herman te Riele . It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.$

In mathematics, an impossibility theorem is a theorem that demonstrates a problem or general set of problems cannot be solved. These are also known as proofs of impossibility, negative proofs, or negative results. Impossibility theorems often resolve decades or centuries of work spent looking for a solution by proving there is no solution. Proving that something is impossible is usually much harder than the opposite task, as it is often necessary to develop a proof that works in general, rather than to just show a particular example. Impossibility theorems are usually expressible as negative existential propositions or universal propositions in logic.

The mathematician Irving Kaplansky is notable for proposing numerous conjectures in several branches of mathematics, including a list of ten conjectures on Hopf algebras. They are usually known as Kaplansky's conjectures.

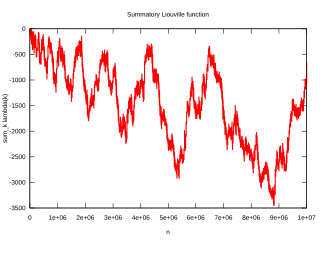
<span class="mw-page-title-main">Pólya conjecture</span> Disproved conjecture in number theory

In number theory, the Pólya conjecture stated that "most" of the natural numbers less than any given number have an odd number of prime factors. The conjecture was set forth by the Hungarian mathematician George Pólya in 1919, and proved false in 1958 by C. Brian Haselgrove. Though mathematicians typically refer to this statement as the Pólya conjecture, Pólya never actually conjectured that the statement was true; rather, he showed that the truth of the statement would imply the Riemann hypothesis. For this reason, it is more accurately called "Pólya's problem".

In logic and mathematics, proof by example is a logical fallacy whereby the validity of a statement is illustrated through one or more examples or cases—rather than a full-fledged proof.

In mathematical programming and polyhedral combinatorics, the Hirsch conjecture is the statement that the edge-vertex graph of an n-facet polytope in d-dimensional Euclidean space has diameter no more than n − d. That is, any two vertices of the polytope must be connected to each other by a path of length at most n − d. The conjecture was first put forth in a letter by Warren M. Hirsch to George B. Dantzig in 1957 and was motivated by the analysis of the simplex method in linear programming, as the diameter of a polytope provides a lower bound on the number of steps needed by the simplex method. The conjecture is now known to be false in general.

<span class="mw-page-title-main">Fermat's Last Theorem</span> 17th-century conjecture proved by Andrew Wiles in 1994

In number theory, Fermat's Last Theorem states that no three positive integers $a$ , $b$ , and $c$ satisfy the equation $a n + b n = c n$ for any integer value of $n$ greater than $2$ . The cases $n = 1$ and $n = 2$ have been known since antiquity to have infinitely many solutions.

Wiles's proof of Fermat's Last Theorem is a proof by British mathematician Andrew Wiles of a special case of the modularity theorem for elliptic curves. Together with Ribet's theorem, it provides a proof for Fermat's Last Theorem. Both Fermat's Last Theorem and the modularity theorem were believed to be impossible to prove using current knowledge by almost all current mathematicians at the time.

<span class="mw-page-title-main">Pythagorean theorem</span> Relation between sides of a right triangle

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

In geometry, Keller's conjecture is the conjecture that in any tiling of $n$ -dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire $(n - 1)$ -dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.

References

1 2 "Mathwords: Counterexample". www.mathwords.com. Retrieved 2019-11-28.
↑ Weisstein, Eric W. "Counterexample". mathworld.wolfram.com. Retrieved 2019-11-28.
↑ "What Is Counterexample?". www.cut-the-knot.org. Retrieved 2019-11-28.
↑ Lander, Parkin (1966). "Counterexample to Euler's conjecture on sums of like powers" (PDF). Bulletin of the American Mathematical Society. 72 (6). Americal Mathematical Society: 1079. doi: 10.1090/s0002-9904-1966-11654-3 . ISSN 0273-0979 . Retrieved 2 August 2018.
↑ Elkies, Noam (October 1988). "On A4 + B4 + C4 = D4" (PDF). Mathematics of Computation. 51 (184): 825–835.

External links

Quotations related to Counterexample at Wikiquote

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 "Mathwords: Counterexample". www.mathwords.com. Retrieved 2019-11-28.

[2] Weisstein, Eric W. "Counterexample". mathworld.wolfram.com. Retrieved 2019-11-28.

[3] "What Is Counterexample?". www.cut-the-knot.org. Retrieved 2019-11-28.

[4] Lander, Parkin (1966). "Counterexample to Euler's conjecture on sums of like powers" (PDF). Bulletin of the American Mathematical Society. 72 (6). Americal Mathematical Society: 1079. doi: 10.1090/s0002-9904-1966-11654-3 . ISSN 0273-0979 . Retrieved 2 August 2018.

[5] Elkies, Noam (October 1988). "On A4 + B4 + C4 = D4" (PDF). Mathematics of Computation. 51 (184): 825–835.

[1]

[2]

[3]

[4]

[5]