
In number theory, a Carmichael number is a composite number , which in modular arithmetic satisfies the congruence relation:

The abc conjecture is a conjecture in number theory that arose out of a discussion of Joseph Oesterlé and David Masser in 1985. It is stated in terms of three positive integers and that are relatively prime and satisfy . The conjecture essentially states that the product of the distinct prime factors of is usually not much smaller than . A number of famous conjectures and theorems in number theory would follow immediately from the abc conjecture or its versions. Mathematician Dorian Goldfeld described the abc conjecture as "The most important unsolved problem in Diophantine analysis".
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.

In number theory, Bertrand's postulate is the theorem that for any integer , there exists at least one prime number with
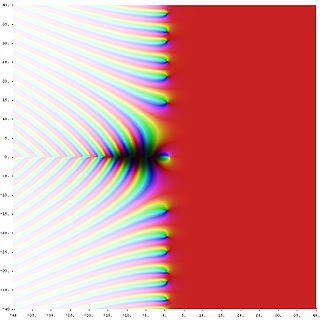
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.
In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936, is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that
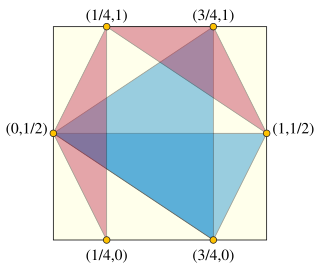
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.
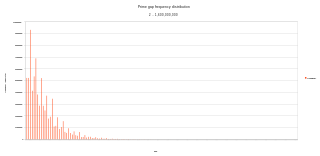
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.

In number theory, the divisor summatory function is a function that is a sum over the divisor function. It frequently occurs in the study of the asymptotic behaviour of the Riemann zeta function. The various studies of the behaviour of the divisor function are sometimes called divisor problems.
In mathematics, the modulus of convexity and the characteristic of convexity are measures of "how convex" the unit ball in a Banach space is. In some sense, the modulus of convexity has the same relationship to the ε-δ definition of uniform convexity as the modulus of continuity does to the ε-δ definition of continuity.
In mathematics, the Johnson–Lindenstrauss lemma is a result named after William B. Johnson and Joram Lindenstrauss concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. In the classical proof of the lemma, the embedding is a random orthogonal projection.
In number theory, specifically the study of Diophantine approximation, the lonely runner conjecture is a conjecture about the long-term behavior of runners on a circular track. It states that runners on a track of unit length, with constant speeds all distinct from one another, will each be lonely at some time—at least units away from all others.

In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery that the pair correlation between pairs of zeros of the Riemann zeta function is
In arithmetic combinatorics, the Erdős–Szemerédi theorem states that for every finite set of integers, at least one of , the set of pairwise sums or , the set of pairwise products form a significantly larger set. More precisely, the Erdős–Szemerédi theorem states that there exist positive constants c and such that for any non-empty set

Michael Jeffrey Larsen is an American mathematician, a distinguished professor of mathematics at Indiana University Bloomington.
In mathematics, a uniformly smooth space is a normed vector space satisfying the property that for every there exists such that if with and then
In number theory, Gillies' conjecture is a conjecture about the distribution of prime divisors of Mersenne numbers and was made by Donald B. Gillies in a 1964 paper in which he also announced the discovery of three new Mersenne primes. The conjecture is a specialization of the prime number theorem and is a refinement of conjectures due to I. J. Good and Daniel Shanks. The conjecture remains an open problem: several papers give empirical support, but it disagrees with the widely accepted Lenstra–Pomerance–Wagstaff conjecture.
The Erdős–Tenenbaum–Ford constant is a mathematical constant that appears in number theory. Named after mathematicians Paul Erdős, Gérald Tenenbaum, and Kevin Ford, it is defined as

Stanisław Knapowski was a Polish mathematician who worked on prime numbers and number theory. Knapowski published 53 papers despite dying at only 36 years old.















