De Finetti's theorem

Last updated

In probability theory, de Finetti's theorem states that exchangeable observations are conditionally independent relative to some latent variable. An epistemic probability distribution could then be assigned to this variable. It is named in honor of Bruno de Finetti.

Contents

For the special case of an exchangeable sequence of Bernoulli random variables it states that such a sequence is a "mixture" of sequences of independent and identically distributed (i.i.d.) Bernoulli random variables.

A sequence of random variables is called exchangeable if the joint distribution of the sequence is unchanged by any permutation of the indices. While the variables of the exchangeable sequence are not themselves independent, only exchangeable, there is an underlying family of i.i.d. random variables. That is, there are underlying, generally unobservable, quantities that are i.i.d. – exchangeable sequences are mixtures of i.i.d. sequences.

Background

A Bayesian statistician often seeks the conditional probability distribution of a random quantity given the data. The concept of exchangeability was introduced by de Finetti. De Finetti's theorem explains a mathematical relationship between independence and exchangeability. [1]

An infinite sequence

of random variables is said to be exchangeable if for any natural number n and any finite sequence i1, ..., in and any permutation of the sequence π:{i1, ..., in } → {i1, ..., in },

both have the same joint probability distribution.

If an identically distributed sequence is independent, then the sequence is exchangeable; however, the converse is false—there exist exchangeable random variables that are not statistically independent, for example the Pólya urn model.

Statement of the theorem

A random variable X has a Bernoulli distribution if Pr(X = 1) = p and Pr(X = 0) = 1 − p for some p ∈ (0, 1).

De Finetti's theorem states that the probability distribution of any infinite exchangeable sequence of Bernoulli random variables is a "mixture" of the probability distributions of independent and identically distributed sequences of Bernoulli random variables. "Mixture", in this sense, means a weighted average, but this need not mean a finite or countably infinite (i.e., discrete) weighted average: it can be an integral rather than a sum.

More precisely, suppose X1, X2, X3, ... is an infinite exchangeable sequence of Bernoulli-distributed random variables. Then there is some probability distribution m on the interval [0, 1] and some random variable Y such that

Another way of stating the theorem

Suppose is an infinite exchangeable sequence of Bernoulli random variables. Then are conditionally independent and identically distributed given the exchangeable sigma-algebra (i.e., the sigma-algebra consisting of events that are measurable with respect to and invariant under finite permutations of the indices).

Example

Here is a concrete example. We construct a sequence

of random variables, by "mixing" two i.i.d. sequences as follows.

We assume p = 2/3 with probability 1/2 and p = 9/10 with probability 1/2. Given the event p = 2/3, the conditional distribution of the sequence is that the Xi are independent and identically distributed and X1 = 1 with probability 2/3 and X1 = 0 with probability 1 − 2/3. Given the event p = 9/10, the conditional distribution of the sequence is that the Xi are independent and identically distributed and X1 = 1 with probability 9/10 and X1 = 0 with probability 1 − 9/10.

This can be interpreted as follows: Make two biased coins, one showing "heads" with 2/3 probability and one showing "heads" with 9/10 probability. Flip a fair coin once to decide which biased coin to use for all flips that are recorded. Here "heads" at flip i means Xi=1.

The independence asserted here is conditional independence, i.e. the Bernoulli random variables in the sequence are conditionally independent given the event that p = 2/3, and are conditionally independent given the event that p = 9/10. But they are not unconditionally independent; they are positively correlated.

In view of the strong law of large numbers, we can say that

Rather than concentrating probability 1/2 at each of two points between 0 and 1, the "mixing distribution" can be any probability distribution supported on the interval from 0 to 1; which one it is depends on the joint distribution of the infinite sequence of Bernoulli random variables.

The definition of exchangeability, and the statement of the theorem, also makes sense for finite length sequences

but the theorem is not generally true in that case. It is true if the sequence can be extended to an exchangeable sequence that is infinitely long. The simplest example of an exchangeable sequence of Bernoulli random variables that cannot be so extended is the one in which X1 = 1 − X2 and X1 is either 0 or 1, each with probability 1/2. This sequence is exchangeable, but cannot be extended to an exchangeable sequence of length 3, let alone an infinitely long one.

Extensions

Versions of de Finetti's theorem for finite exchangeable sequences, [2] [3] and for Markov exchangeable sequences [4] have been proved by Diaconis and Freedman and by Kerns and Szekely. Two notions of partial exchangeability of arrays, known as separate and joint exchangeability lead to extensions of de Finetti's theorem for arrays by Aldous and Hoover. [5]

The computable de Finetti theorem shows that if an exchangeable sequence of real random variables is given by a computer program, then a program which samples from the mixing measure can be automatically recovered. [6]

In the setting of free probability, there is a noncommutative extension of de Finetti's theorem which characterizes noncommutative sequences invariant under quantum permutations. [7]

Extensions of de Finetti's theorem to quantum states have been found to be useful in quantum information, [8] [9] [10] in topics like quantum key distribution [11] and entanglement detection. [12] A multivariate extension of de Finetti’s theorem can be used to derive Bose–Einstein statistics from the statistics of classical (i.e. independent) particles. [13]

See also

Related Research Articles

<span class="mw-page-title-main">Expected value</span> Average value of a random variable

In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable.

<span class="mw-page-title-main">Entropy (information theory)</span> Expected amount of information needed to specify the output of a stochastic data source

In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable , which takes values in the alphabet and is distributed according to :

<span class="mw-page-title-main">Probability theory</span> Branch of mathematics concerning probability

Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.

<span class="mw-page-title-main">Probability distribution</span> Mathematical function for the probability a given outcome occurs in an experiment

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

In probability theory, the central limit theorem (CLT) establishes that, in many situations, for independent and identically distributed random variables, the sampling distribution of the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.

<span class="mw-page-title-main">Bernoulli process</span> Random process of binary (boolean) random variables

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesXi are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable Xi in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

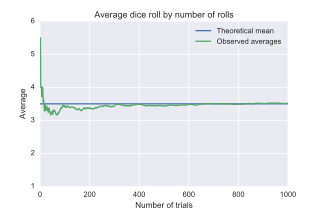
<span class="mw-page-title-main">Law of large numbers</span> Averages of repeated trials converge to the expected value

In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed.

In probability theory, Kolmogorov's zero–one law, named in honor of Andrey Nikolaevich Kolmogorov, specifies that a certain type of event, namely a tail event of independent σ-algebras, will either almost surely happen or almost surely not happen; that is, the probability of such an event occurring is zero or one.

In mathematics and statistics, an asymptotic distribution is a probability distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators.

In probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable:Z = X + Y. If, further, it can be expressed as the distribution of the sum of two or more independent identically distributed random variables, then it is divisible:Z = X1 + X2.

The Hewitt–Savage zero–one law is a theorem in probability theory, similar to Kolmogorov's zero–one law and the Borel–Cantelli lemma, that specifies that a certain type of event will either almost surely happen or almost surely not happen. It is sometimes known as the Savage-Hewitt law for symmetric events. It is named after Edwin Hewitt and Leonard Jimmie Savage.

In statistics, an exchangeable sequence of random variables is a sequence X1, X2, X3, ... whose joint probability distribution does not change when the positions in the sequence in which finitely many of them appear are altered. Thus, for example the sequences

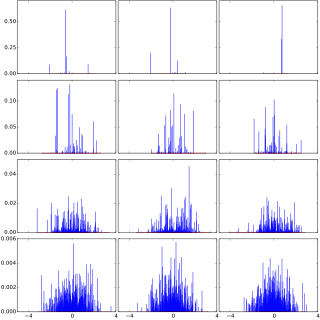
<span class="mw-page-title-main">Dirichlet process</span> Family of stochastic processes

In probability theory, Dirichlet processes are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose range is itself a set of probability distributions. It is often used in Bayesian inference to describe the prior knowledge about the distribution of random variables—how likely it is that the random variables are distributed according to one or another particular distribution.

In probability theory, a probability distribution is infinitely divisible if it can be expressed as the probability distribution of the sum of an arbitrary number of independent and identically distributed (i.i.d.) random variables. The characteristic function of any infinitely divisible distribution is then called an infinitely divisible characteristic function.

This page lists articles related to probability theory. In particular, it lists many articles corresponding to specific probability distributions. Such articles are marked here by a code of the form (X:Y), which refers to number of random variables involved and the type of the distribution. For example (2:DC) indicates a distribution with two random variables, discrete or continuous. Other codes are just abbreviations for topics. The list of codes can be found in the table of contents.

In statistics, asymptotic theory, or large sample theory, is a framework for assessing properties of estimators and statistical tests. Within this framework, it is often assumed that the sample size n may grow indefinitely; the properties of estimators and tests are then evaluated under the limit of n → ∞. In practice, a limit evaluation is considered to be approximately valid for large finite sample sizes too.

In statistics, a Pólya urn model, named after George Pólya, is a family of urn models that can be used to interpret many commonly used statistical models.

In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usually abbreviated as i.i.d., iid, or IID. IID was first defined in statistics and finds application in different fields such as data mining and signal processing.

References

  1. ↑ See the Oxford lecture notes of Steffen Lauritzen http://www.stats.ox.ac.uk/~steffen/teaching/grad/definetti.pdf
  2. ↑ Diaconis, P.; Freedman, D. (1980). "Finite exchangeable sequences". Annals of Probability. 8 (4): 745–764. doi: 10.1214/aop/1176994663 . MR   0577313. Zbl   0434.60034.
  3. ↑ Szekely, G. J.; Kerns, J. G. (2006). "De Finetti's theorem for abstract finite exchangeable sequences". Journal of Theoretical Probability. 19 (3): 589–608. doi:10.1007/s10959-006-0028-z. S2CID   119981020.
  4. ↑ Diaconis, P.; Freedman, D. (1980). "De Finetti's theorem for Markov chains". Annals of Probability. 8 (1): 115–130. doi: 10.1214/aop/1176994828 . MR   0556418. Zbl   0426.60064.
  5. ↑ Persi Diaconis and Svante Janson (2008) "Graph Limits and Exchangeable Random Graphs",Rendiconti di Matematica, Ser. VII 28(1), 33–61.
  6. ↑ Cameron Freer and Daniel Roy (2009) "Computable exchangeable sequences have computable de Finetti measures", Proceedings of the 5th Conference on Computability in Europe: Mathematical Theory and Computational Practice, Lecture Notes in Computer Science, Vol. 5635, pp. 218–231.
  7. ↑ Koestler, Claus; Speicher, Roland (2009). "A noncommutative de Finetti theorem: Invariance under quantum permutations is equivalent to freeness with amalgamation". Commun. Math. Phys. 291 (2): 473–490. arXiv: 0807.0677 . Bibcode:2009CMaPh.291..473K. doi:10.1007/s00220-009-0802-8. S2CID   115155584.
  8. ↑ Caves, Carlton M.; Fuchs, Christopher A.; Schack, Ruediger (2002-08-20). "Unknown quantum states: The quantum de Finetti representation". Journal of Mathematical Physics. 43 (9): 4537–4559. arXiv: quant-ph/0104088 . Bibcode:2002JMP....43.4537C. doi:10.1063/1.1494475. ISSN   0022-2488. S2CID   17416262.
  9. ↑ J. Baez (2007). "This Week's Finds in Mathematical Physics (Week 251)" . Retrieved 29 April 2012.
  10. ↑ Brandao, Fernando G.S.L.; Harrow, Aram W. (2013-01-01). "Quantum de finetti theorems under local measurements with applications". Proceedings of the forty-fifth annual ACM symposium on Theory of Computing. STOC '13. New York, NY, USA: ACM. pp. 861–870. arXiv: 1210.6367 . doi:10.1145/2488608.2488718. ISBN   9781450320290. S2CID   1772280.
  11. ↑ Renner, Renato (2005-12-30). "Security of Quantum Key Distribution". arXiv: quant-ph/0512258 .
  12. ↑ Doherty, Andrew C.; Parrilo, Pablo A.; Spedalieri, Federico M. (2005-01-01). "Detecting multipartite entanglement". Physical Review A. 71 (3): 032333. arXiv: quant-ph/0407143 . Bibcode:2005PhRvA..71c2333D. doi:10.1103/PhysRevA.71.032333. S2CID   44241800.
  13. ↑ Bach, A.; Blank, H.; Francke, H. (1985). "Bose-Einstein statistics derived from the statistics of classical particles". Lettere al Nuovo Cimento. 43 (4): 195–198. doi:10.1007/BF02746978. S2CID   121413539.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.