
In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.

In calculus, Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the kth-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order k of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.

A logistic function or logistic curve is a common S-shaped curve with equation
In mathematics, Itô's lemma or Itô's formula is an identity used in Itô calculus to find the differential of a time-dependent function of a stochastic process. It serves as the stochastic calculus counterpart of the chain rule. It can be heuristically derived by forming the Taylor series expansion of the function up to its second derivatives and retaining terms up to first order in the time increment and second order in the Wiener process increment. The lemma is widely employed in mathematical finance, and its best known application is in the derivation of the Black–Scholes equation for option values.

Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of gravity (cg), known as pitch, roll and yaw. These are collectively known as aircraft attitude, often principally relative to the atmospheric frame in normal flight, but also relative to terrain during takeoff or landing, or when operating at low elevation. The concept of attitude is not specific to fixed-wing aircraft, but also extends to rotary aircraft such as helicopters, and dirigibles, where the flight dynamics involved in establishing and controlling attitude are entirely different.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival?

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In mathematical finance, a risk-neutral measure is a probability measure such that each share price is exactly equal to the discounted expectation of the share price under this measure. This is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market, a derivative's price is the discounted expected value of the future payoff under the unique risk-neutral measure. Such a measure exists if and only if the market is arbitrage-free.
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation. The method is to reduce a partial differential equation to a family of ordinary differential equations along which the solution can be integrated from some initial data given on a suitable hypersurface.
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R,. People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again.

Stability derivatives, and also control derivatives, are measures of how particular forces and moments on an aircraft change as other parameters related to stability change. For a defined "trim" flight condition, changes and oscillations occur in these parameters. Equations of motion are used to analyze these changes and oscillations. Stability and control derivatives are used to linearize (simplify) these equations of motion so the stability of the vehicle can be more readily analyzed.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.

In mathematical finance, the Black–Scholes equation is a partial differential equation (PDE) governing the price evolution of a European call or European put under the Black–Scholes model. Broadly speaking, the term may refer to a similar PDE that can be derived for a variety of options, or more generally, derivatives.

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways..
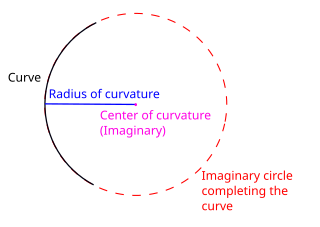
In differential geometry, the radius of curvature (Rc), R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.












































