Related Research Articles
Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.
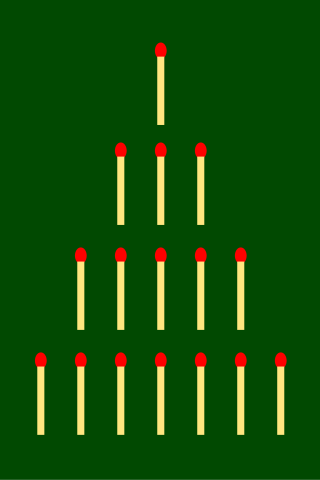
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.
In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a one-heap game of nim, or to an infinite generalization of nim. It can therefore be represented as a natural number, the size of the heap in its equivalent game of nim, as an ordinal number in the infinite generalization, or alternatively as a nimber, the value of that one-heap game in an algebraic system whose addition operation combines multiple heaps to form a single equivalent heap in nim.

In mathematics, the surreal number system is a totally ordered proper class containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. The surreals share many properties with the reals, including the usual arithmetic operations ; as such, they form an ordered field. If formulated in von Neumann–Bernays–Gödel set theory, the surreal numbers are a universal ordered field in the sense that all other ordered fields, such as the rationals, the reals, the rational functions, the Levi-Civita field, the superreal numbers can be realized as subfields of the surreals. The surreals also contain all transfinite ordinal numbers; the arithmetic on them is given by the natural operations. It has also been shown that the maximal class hyperreal field is isomorphic to the maximal class surreal field.
In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric. In other words, the only difference between player 1 and player 2 is that player 1 goes first. The game is played until a terminal position is reached. A terminal position is one from which no moves are possible. Then one of the players is declared the winner and the other the loser. Furthermore, impartial games are played with perfect information and no chance moves, meaning all information about the game and operations for both players are visible to both players.
In mathematics, the nimbers, also called Grundy numbers, are introduced in combinatorial game theory, where they are defined as the values of heaps in the game Nim. The nimbers are the ordinal numbers endowed with nimber addition and nimber multiplication, which are distinct from ordinal addition and ordinal multiplication.

Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.
In combinatorial game theory, a game is partisan if it is not impartial. That is, some moves are available to one player and not to the other.

Abstract strategy games admit a number of definitions which distinguish these from strategy games in general, mostly involving no or minimal narrative theme, outcomes determined only by player choice, and perfect information. For example, Go is a pure abstract strategy game since it fulfills all three criteria; chess and related games are nearly so but feature a recognizable theme of ancient warfare; and Stratego is borderline since it is deterministic, loosely based on 19th-century Napoleonic warfare, and features concealed information.
In combinatorial game theory, the zero game is the game where neither player has any legal options. Therefore, under the normal play convention, the first player automatically loses, and it is a second-player win. The zero game has a Sprague–Grundy value of zero. The combinatorial notation of the zero game is: { | }.
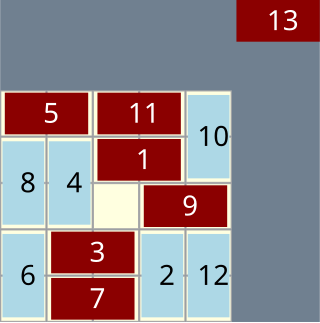
Domineering is a mathematical game that can be played on any collection of squares on a sheet of graph paper. For example, it can be played on a 6×6 square, a rectangle, an entirely irregular polyomino, or a combination of any number of such components. Two players have a collection of dominoes which they place on the grid in turn, covering up squares. One player places tiles vertically, while the other places them horizontally. As in most games in combinatorial game theory, the first player who cannot move loses.

Hackenbush is a two-player game invented by mathematician John Horton Conway. It may be played on any configuration of colored line segments connected to one another by their endpoints and to a "ground" line.

Several map-coloring games are studied in combinatorial game theory. The general idea is that we are given a map with regions drawn in but with not all the regions colored. Two players, Left and Right, take turns coloring in one uncolored region per turn, subject to various constraints. The move constraints and the winning condition are features of the particular game.
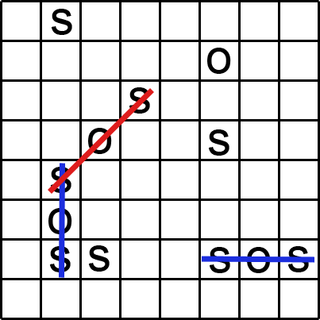
SOS is paper and pencil game for two or more players. It is similar to tic-tac-toe and dots and boxes, but has greater complexity.

Kayles is a simple impartial game in combinatorial game theory, invented by Henry Dudeney in 1908. Given a row of imagined bowling pins, players take turns to knock out either one pin, or two adjacent pins, until all the pins are gone. Using the notation of octal games, Kayles is denoted 0.77.
The octal games are a class of two-player games that involve removing tokens from heaps of tokens. They have been studied in combinatorial game theory as a generalization of Nim, Kayles, and similar games.
In the mathematical theory of games, genus theory in impartial games is a theory by which some games played under the misère play convention can be analysed, to predict the outcome class of games.
In combinatorial game theory, and particularly in the theory of impartial games in misère play, an indistinguishability quotient is a commutative monoid that generalizes and localizes the Sprague–Grundy theorem for a specific game's rule set.
In combinatorial game theory, a branch of mathematics, a hot game is one in which each player can improve their position by making the next move.
In combinatorial game theory, a subtraction game is an abstract strategy game whose state can be represented by a natural number or vector of numbers and in which the allowed moves reduce these numbers. Often, the moves of the game allow any number to be reduced by subtracting a value from a specified subtraction set, and different subtraction games vary in their subtraction sets. These games also vary in whether the last player to move wins or loses (misère). Another winning convention that has also been used is that a player who moves to a position with all numbers zero wins, but that any other position with no moves possible is a draw.
References
- Conway, John Horton (1976), On Numbers and Games , Academic Press.