
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 1015 K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 1015 K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5x1012 K (from the Large Hadron Collider).

In mathematics, a self-similar object is exactly or approximately similar to a part of itself. Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales. Self-similarity is a typical property of fractals. Scale invariance is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar to the whole. For instance, a side of the Koch snowflake is both symmetrical and scale-invariant; it can be continually magnified 3x without changing shape. The non-trivial similarity evident in fractals is distinguished by their fine structure, or detail on arbitrarily small scales. As a counterexample, whereas any portion of a straight line may resemble the whole, further detail is not revealed.

Technicolor theories are models of physics beyond the Standard Model that address electroweak gauge symmetry breaking, the mechanism through which W and Z bosons acquire masses. Early technicolor theories were modelled on quantum chromodynamics (QCD), the "color" theory of the strong nuclear force, which inspired their name.

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.
Quantum metrology is the study of making high-resolution and highly sensitive measurements of physical parameters using quantum theory to describe the physical systems, particularly exploiting quantum entanglement and quantum squeezing. This field promises to develop measurement techniques that give better precision than the same measurement performed in a classical framework. Together with quantum hypothesis testing, it represents an important theoretical model at the basis of quantum sensing.
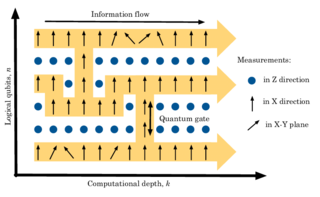
The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal, gamma and inverse Gaussian distributions, the purely discrete scaled Poisson distribution, and the class of compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. Tweedie distributions are a special case of exponential dispersion models and are often used as distributions for generalized linear models.
In applied mathematics, the numerical sign problem is the problem of numerically evaluating the integral of a highly oscillatory function of a large number of variables. Numerical methods fail because of the near-cancellation of the positive and negative contributions to the integral. Each has to be integrated to very high precision in order for their difference to be obtained with useful accuracy.

Active matter is matter composed of large numbers of active "agents", each of which consumes energy in order to move or to exert mechanical forces. Such systems are intrinsically out of thermal equilibrium. Unlike thermal systems relaxing towards equilibrium and systems with boundary conditions imposing steady currents, active matter systems break time reversal symmetry because energy is being continually dissipated by the individual constituents. Most examples of active matter are biological in origin and span all the scales of the living, from bacteria and self-organising bio-polymers such as microtubules and actin, to schools of fish and flocks of birds. However, a great deal of current experimental work is devoted to synthetic systems such as artificial self-propelled particles. Active matter is a relatively new material classification in soft matter: the most extensively studied model, the Vicsek model, dates from 1995.
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian
In theoretical physics, the logarithmic Schrödinger equation is one of the nonlinear modifications of Schrödinger's equation. It is a classical wave equation with applications to extensions of quantum mechanics, quantum optics, nuclear physics, transport and diffusion phenomena, open quantum systems and information theory, effective quantum gravity and physical vacuum models and theory of superfluidity and Bose–Einstein condensation. Its relativistic version was first proposed by Gerald Rosen. It is an example of an integrable model.
The Vicsek model is a mathematical model used to describe active matter. One motivation of the study of active matter by physicists is the rich phenomenology associated to this field. Collective motion and swarming are among the most studied phenomena. Within the huge number of models that have been developed to catch such behavior from a microscopic description, the most famous is the model introduced by Tamás Vicsek et al. in 1995.
Linear optical quantum computing or linear optics quantum computation (LOQC) is a paradigm of quantum computation, allowing universal quantum computation. LOQC uses photons as information carriers, mainly uses linear optical elements, or optical instruments to process quantum information, and uses photon detectors and quantum memories to detect and store quantum information.
Physicists often use various lattices to apply their favorite models in them. For instance, the most favorite lattice is perhaps the square lattice. There are 14 Bravais space lattice where every cell has exactly the same number of nearest, next nearest, nearest of next nearest etc. neighbors and hence they are called regular lattice. Often physicists and mathematicians study phenomena which require disordered lattice where each cell do not have exactly the same number of neighbors rather the number of neighbors can vary wildly. For instance, if one wants to study the spread of disease, viruses, rumors etc. then the last thing one would look for is the square lattice. In such cases a disordered lattice is necessary. One way of constructing a disordered lattice is by doing the following.
The KLM scheme or KLM protocol is an implementation of linear optical quantum computing (LOQC), developed in 2000 by Emanuel Knill, Raymond Laflamme and Gerard J. Milburn. This protocol makes it possible to create universal quantum computers solely with linear optical tools. The KLM protocol uses linear optical elements, single-photon sources and photon detectors as resources to construct a quantum computation scheme involving only ancilla resources, quantum teleportations and error corrections.
Supersymmetric theory of stochastic dynamics or stochastics (STS) is an exact theory of stochastic (partial) differential equations (SDEs), the class of mathematical models with the widest applicability covering, in particular, all continuous time dynamical systems, with and without noise. The main utility of the theory from the physical point of view is a rigorous theoretical explanation of the ubiquitous spontaneous long-range dynamical behavior that manifests itself across disciplines via such phenomena as 1/f, flicker, and crackling noises and the power-law statistics, or Zipf's law, of instantonic processes like earthquakes and neuroavalanches. From the mathematical point of view, STS is interesting because it bridges the two major parts of mathematical physics – the dynamical systems theory and topological field theories. Besides these and related disciplines such as algebraic topology and supersymmetric field theories, STS is also connected with the traditional theory of stochastic differential equations and the theory of pseudo-Hermitian operators.
In the theory of dynamical systems, a bailout embedding is a system defined as
The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. The quantum Fisher information of a state with respect to the observable is defined as
A set of networks that satisfies given structural characteristics can be treated as a network ensemble. Brought up by Ginestra Bianconi in 2007, the entropy of a network ensemble measures the level of the order or uncertainty of a network ensemble.




















