Related Research Articles

Ronald Lewis Graham was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.

Martin David Davis was an American mathematician and computer scientist who contributed to the fields of computability theory and mathematical logic. His work on Hilbert's tenth problem led to the MRDP theorem. He also advanced the Post–Turing model and co-developed the Davis–Putnam–Logemann–Loveland (DPLL) algorithm, which is foundational for Boolean satisfiability solvers.

Sir Vaughan Frederick Randal Jones was a New Zealand mathematician known for his work on von Neumann algebras and knot polynomials. He was awarded a Fields Medal in 1990.

Robin James Wilson is an English mathematician. He is an emeritus professor in the Department of Mathematics at the Open University, having previously been Head of the Pure Mathematics Department and Dean of the Faculty. He was a stipendiary lecturer at Pembroke College, Oxford and, as of 2006, Gresham Professor of Geometry at Gresham College, London, where he has also been a visiting professor. On occasion, he teaches at Colorado College in the United States. He is also a long standing fellow of Keble College, Oxford.

In mathematics, Scheinerman's conjecture, now a theorem, states that every planar graph is the intersection graph of a set of line segments in the plane. This conjecture was formulated by E. R. Scheinerman in his Ph.D. thesis (1984), following earlier results that every planar graph could be represented as the intersection graph of a set of simple curves in the plane. It was proven by Jeremie Chalopin and Daniel Gonçalves.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.
In mathematics, a representation is a very general relationship that expresses similarities between mathematical objects or structures. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the representing objects yi conform, in some consistent way, to those existing among the corresponding represented objects xi. More specifically, given a set Π of properties and relations, a Π-representation of some structure X is a structure Y that is the image of X under a homomorphism that preserves Π. The label representation is sometimes also applied to the homomorphism itself.
Carsten Thomassen is a Danish mathematician. He has been a Professor of Mathematics at the Technical University of Denmark since 1981, and since 1990 a member of the Royal Danish Academy of Sciences and Letters. His research concerns discrete mathematics and more specifically graph theory.
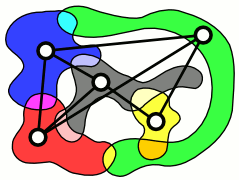
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.

In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.
In graph theory, a string graph is an intersection graph of curves in the plane; each curve is called a "string". Given a graph G, G is a string graph if and only if there exists a set of curves, or strings, such that the graph having a vertex for each curve and an edge for each intersecting pair of curves is isomorphic to G.
Steven Lawrence Kleiman is an American mathematician.

In graph theory, the crossing numbercr(G) of a graph G is the lowest number of edge crossings of a plane drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing.
Douglas Brent West is a professor of graph theory at University of Illinois at Urbana-Champaign. He received his Ph.D. from Massachusetts Institute of Technology in 1978; his advisor was Daniel Kleitman. He is the "W" in G. W. Peck, a pseudonym for a group of six mathematicians that includes West. He is the editor of the journal Discrete Mathematics.
In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.
A dot product representation of a simple graph is a method of representing a graph using vector spaces and the dot product from linear algebra. Every graph has a dot product representation.
Zdeněk Dvořák is a Czech mathematician specializing in graph theory.
Ann Natalie Trenk is an American mathematician interested in graph theory and the theory of partially ordered sets, and known for her research on proper distinguishing colorings of graphs and on tolerance graphs. She is the Lewis Atterbury Stimson Professor of Mathematics at Wellesley College.
Pearls in Graph Theory: A Comprehensive Introduction is an undergraduate-level textbook on graph theory by Nora Hartsfield and Gerhard Ringel. It was published in 1990 by Academic Press with a revised edition in 1994 and a paperback reprint of the revised edition by Dover Books in 2003. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.
References
- 1 2 3 4 Faculty profile, Johns Hopkins University, retrieved 2013-07-12.
- ↑ Chalopin, J.; Gonçalves, D. (2009), "Every planar graph is the intersection graph of segments in the plane" (PDF), ACM Symposium on Theory of Computing .
- ↑ Ed Scheinerman at the Mathematics Genealogy Project
- ↑ List of Ford Award winners Archived 1999-09-10 at the Wayback Machine , MAA, retrieved 2013-07-12.
- ↑ List of Fellows of the American Mathematical Society, retrieved 2013-07-12.
- ↑ Review of Fractional Graph Theory, MR 1481157 and MR 2963519.