Eight-vertex model

Last updated March 24, 2021

In statistical mechanics, the eight-vertex model is a generalisation of the ice-type (six-vertex) models; it was discussed by Sutherland,^[1] and Fan & Wu,^[2] and solved by Baxter in the zero-field case.^[3]

Description

As with the ice-type models, the eight-vertex model is a square lattice model, where each state is a configuration of arrows at a vertex. The allowed vertices have an even number of arrows pointing towards the vertex; these include the six inherited from the ice-type model (1-6), and sinks and sources (7, 8).

Eightvertex2 Eightvertex2.png — Eightvertex2

We consider a $N\times N$ lattice, with $N^{2}$ vertices and $2N^{2}$ edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex $j$ has an associated energy $\epsilon _{j}$ and Boltzmann weight $w_{j}=e^{-{\frac {\epsilon _{j}}{kT}}}$ , giving the partition function over the lattice as

Z=\sum \exp \left(-{\frac {\sum _{j}n_{j}\epsilon _{j}}{kT}}\right)

where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.

Solution in the zero-field case

The zero-field case of the model corresponds physically to the absence of external electric fields. Hence, the model remains unchanged under the reversal of all arrows; the states 1 and 2, and 3 and 4, consequently must occur as pairs. The vertices can be assigned arbitrary weights

{\begin{aligned}w_{1}=w_{2}&=a\\w_{3}=w_{4}&=b\\w_{5}=w_{6}&=c\\w_{7}=w_{8}&=d.\end{aligned}}

The solution is based on the observation that rows in transfer matrices commute, for a certain parametrisation of these four Boltzmann weights. This came about as a modification of an alternate solution for the six-vertex model; it makes use of elliptic theta functions.

Commuting transfer matrices

The proof relies on the fact that when $\Delta '=\Delta$ and $\Gamma '=\Gamma$ , for quantities

{\begin{aligned}\Delta &={\frac {a^{2}+b^{2}-c^{2}-d^{2}}{2(ab+cd)}}\\\Gamma &={\frac {ab-cd}{ab+cd}}\end{aligned}}

the transfer matrices $T$ and $T'$ (associated with the weights $a$ , $b$ , $c$ , $d$ and $a'$ , $b'$ , $c'$ , $d'$ ) commute. Using the star-triangle relation, Baxter reformulated this condition as equivalent to a parametrisation of the weights given as

a:b:c:d=\operatorname {snh} (\eta -u):\operatorname {snh} (\eta +u):\operatorname {snh} (2\eta ):k\operatorname {snh} (2\eta )\operatorname {snh} (\eta -u)\operatorname {snh} (\eta +u)

for fixed modulus $k$ and $\eta$ and variable $u$ . Here snh is the hyperbolic analogue of sn, given by

{\begin{aligned}\operatorname {snh} (u)&=-i\operatorname {snh} (iu)\\{\text{where }}\operatorname {snh} (u)&={\frac {H(u)}{k^{1/2}\Theta (u)}}\end{aligned}}

and $H(u)$ and $\Theta (u)$ are Jacobi elliptic functions of modulus $k$ . The associated transfer matrix $T$ thus is a function of $u$ alone; for all $u$ , $v$

T(u)T(v)=T(v)T(u).

The matrix function $Q(u)$

The other crucial part of the solution is the existence of a nonsingular matrix-valued function $Q$ , such that for all complex $u$ the matrices $Q(u),Q(u')$ commute with each other and the transfer matrices, and satisfy

\zeta (u)T(u)Q(u)=\phi (u-\eta )Q(u+2\eta )+\phi (u+\eta )Q(u-2\eta )

(1)

where

{\begin{aligned}\zeta (u)&=[c^{-1}H(2\eta )\Theta (u-\eta )\Theta (u+\eta )]^{N}\\\phi (u)&=[\Theta (0)H(u)\Theta (u)]^{N}.\end{aligned}}

The existence and commutation relations of such a function are demonstrated by considering pair propagations through a vertex, and periodicity relations of the theta functions, in a similar way to the six-vertex model.

Explicit solution

The commutation of matrices in ( 1 ) allow them to be diagonalised, and thus eigenvalues can be found. The partition function is calculated from the maximal eigenvalue, resulting in a free energy per site of

{\begin{aligned}f=\epsilon _{5}-2kT\sum _{n=1}^{\infty }{\frac {\sinh ^{2}((\tau -\lambda )n)(\cosh(n\lambda )-\cosh(n\alpha ))}{n\sinh(2n\tau )\cosh(n\lambda )}}\end{aligned}}

for

{\begin{aligned}\tau &={\frac {\pi K'}{2K}}\\\lambda &={\frac {\pi \eta }{iK}}\\\alpha &={\frac {\pi u}{iK}}\end{aligned}}

where $K$ and $K'$ are the complete elliptic integrals of moduli $k$ and $k'$ . The eight vertex model was also solved in quasicrystals.

Equivalence with an Ising model

There is a natural correspondence between the eight-vertex model, and the Ising model with 2-spin and 4-spin nearest neighbour interactions. The states of this model are spins $\sigma =\pm 1$ on faces of a square lattice. The analogue of 'edges' in the eight-vertex model are products of spins on adjacent faces:

{\begin{aligned}\alpha _{ij}&=\sigma _{ij}\sigma _{i,j+1}\\\mu _{ij}&=\sigma _{ij}\sigma _{i+1,j}.\end{aligned}}

The most general form of the energy for this model is

{\begin{aligned}\epsilon &=-\sum _{ij}(J_{h}\mu _{ij}+J_{v}\alpha _{ij}+J\alpha _{ij}\mu _{ij}+J'\alpha _{i+1,j}\mu _{ij}+J''\alpha _{ij}\alpha _{i+1,j})\end{aligned}}

where $J_{h}$ , $J_{v}$ , $J$ , $J'$ describe the horizontal, vertical and two diagonal 2-spin interactions, and $J''$ describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.

We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model $\mu$ , $\alpha$ respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each $\sigma$ configuration then corresponds to a unique $\mu$ , $\alpha$ configuration, whereas each $\mu$ , $\alpha$ configuration gives two choices of $\sigma$ configurations.

Equating general forms of Boltzmann weights for each vertex $j$ , the following relations between the $\epsilon _{j}$ and $J_{h}$ , $J_{v}$ , $J$ , $J'$ , $J''$ define the correspondence between the lattice models:

{\begin{aligned}\epsilon _{1}&=-J_{h}-J_{v}-J-J'-J'',\quad \epsilon _{2}=J_{h}+J_{v}-J-J'-J''\\\epsilon _{3}&=-J_{h}+J_{v}+J+J'-J'',\quad \epsilon _{4}=J_{h}-J_{v}+J+J'-J''\\\epsilon _{5}&=\epsilon _{6}=J-J'+J''\\\epsilon _{7}&=\epsilon _{8}=-J+J'+J''.\end{aligned}}

It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.

These relations gives the equivalence $Z_{I}=2Z_{8V}$ between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.

Notes

↑ Sutherland, Bill (1970). "Two‐Dimensional Hydrogen Bonded Crystals without the Ice Rule". Journal of Mathematical Physics. AIP Publishing. 11 (11): 3183–3186. Bibcode:1970JMP....11.3183S. doi:10.1063/1.1665111. ISSN 0022-2488.
↑ Fan, Chungpeng; Wu, F. Y. (1970-08-01). "General Lattice Model of Phase Transitions". Physical Review B. American Physical Society (APS). 2 (3): 723–733. Bibcode:1970PhRvB...2..723F. doi:10.1103/physrevb.2.723. ISSN 0556-2805.
↑ Baxter, R. J. (1971-04-05). "Eight-Vertex Model in Lattice Statistics". Physical Review Letters. American Physical Society (APS). 26 (14): 832–833. Bibcode:1971PhRvL..26..832B. doi:10.1103/physrevlett.26.832. ISSN 0031-9007.

Related Research Articles

In mathematical physics and mathematics, the Pauli matrices are a set of three $2 \times 2$ complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries. They are

In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol represents a collection of numbers; defined from the sign of a permutation of the natural numbers $1, 2, \dots, n$ , for some positive integer $n$ . It is named after the Italian mathematician and physicist Tullio Levi-Civita. Other names include the permutation symbol, antisymmetric symbol, or alternating symbol, which refer to its antisymmetric property and definition in terms of permutations.

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.

Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.

In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: properly, an exponential family is a set of distributions, where the specific distribution varies with the parameter; however, a parametric family of distributions is often referred to as "a distribution", and the set of all exponential families is sometimes loosely referred to as "the" exponential family.

In statistics, the Neyman–Pearson lemma was introduced by Jerzy Neyman and Egon Pearson in a paper in 1933. The Neyman-Pearson lemma is part of the Neyman-Pearson theory of statistical testing, which introduced concepts like errors of the second kind, power function, and inductive behavior. The previous Fisherian theory of significance testing postulated only one hypothesis. By introducing a competing hypothesis, the Neyman-Pearsonian flavor of statistical testing allows investigating the two types of errors. The trivial cases where one always rejects or accepts the null hypothesis are of little interest but it does prove that one must not relinquish control over one type of error while calibrating the other. Neyman and Pearson accordingly proceeded to restrict their attention to the class of all $level tests while subsequently minimizing type II error, traditionally denoted by . Their seminal paper of 1933, including the Neyman-Pearson lemma, comes at the end of this endeavor, not only showing the existence of tests with the most power that retain a prespecified level of type I error, but also providing a way to construct such tests. The Karlin-Rubin theorem extends the Neyman-Pearson lemma to settings involving composite hypotheses with monotone likelihood ratios.$

In mathematical physics, the gamma matrices, $, also known as the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra C ℓ 1,3 (R). It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin-½ particles.$

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.

In statistical mechanics, the two-dimensional square lattice Ising model is a simple lattice model of interacting magnetic spins. The model is notable for having nontrivial interactions, yet having an analytical solution. The model was solved by Lars Onsager for the special case that the external magnetic field H = 0.(Onsager ) An analytical solution for the general case for $has yet to be found.$

The history of Lorentz transformations comprises the development of linear transformations forming the Lorentz group or Poincaré group preserving the Lorentz interval $and the Minkowski inner product .$

In linear regression, mean response and predicted response are values of the dependent variable calculated from the regression parameters and a given value of the independent variable. The values of these two responses are the same, but their calculated variances are different.

In mathematics, the Rudin–Shapiro sequence, also known as the Golay–Rudin–Shapiro sequence, is an infinite 2-automatic sequence named after Marcel Golay, Walter Rudin, and Harold S. Shapiro, who independently investigated its properties.

The purpose of this page is to provide supplementary materials for the ordinary least squares article, reducing the load of the main article with mathematics and improving its accessibility, while at the same time retaining the completeness of exposition.

In statistics, errors-in-variables models or measurement error models are regression models that account for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been measured exactly, or observed without error; as such, those models account only for errors in the dependent variables, or responses.

The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Centuries passed before more extensive trigonometric tables were created. One such table is the Canon Sinuum created at the end of the 16th century.

In computational chemistry and molecular dynamics, the combination rules or combining rules are equations that provide the interaction energy between two dissimilar non-bonded atoms, usually for the part of the potential representing the van der Waals interaction. In the simulation of mixtures, the choice of combining rules can sometimes affect the outcome of the simulation.

$imbalance$ is a performance-limiting issue in the design of direct conversion receivers, also known as zero intermediate frequency (IF) or homodyne receivers. Such a design translates the received radio frequency signal directly from the carrier frequency to baseband using only one mixing stage. The traditional heterodyne receiver structure needs an IF stage between the RF and baseband signals. The direct conversion receiver structure does not have an IF stage and does not need an image rejection filter. Due to the lower component count, it is easier to integrate. However, a direct-conversion RF front-end suffers from two major drawbacks: one is $imbalance$ and the other is DC offset. When designing a homodyne receiver, control of $imbalance is necessary to limit signal demodulation error.$

A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy-momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.

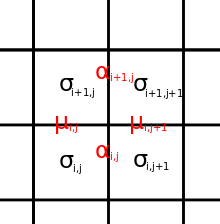
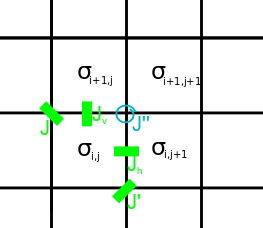
The two-dimensional critical Ising model is the critical limit of the Ising model in two dimensions. It is a two-dimensional conformal field theory whose symmetry algebra is the Virasoro algebra with the central charge $. Correlation functions of the spin and energy operators are described by the minimal model. While the minimal model has been exactly solved, the solution does not cover other observables such as connectivities of clusters.$

References

Baxter, Rodney J. (1982), Exactly solved models in statistical mechanics (PDF), London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, MR 0690578

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Sutherland, Bill (1970). "Two‐Dimensional Hydrogen Bonded Crystals without the Ice Rule". Journal of Mathematical Physics. AIP Publishing. 11 (11): 3183–3186. Bibcode:1970JMP....11.3183S. doi:10.1063/1.1665111. ISSN 0022-2488.

[2] Fan, Chungpeng; Wu, F. Y. (1970-08-01). "General Lattice Model of Phase Transitions". Physical Review B. American Physical Society (APS). 2 (3): 723–733. Bibcode:1970PhRvB...2..723F. doi:10.1103/physrevb.2.723. ISSN 0556-2805.

[3] Baxter, R. J. (1971-04-05). "Eight-Vertex Model in Lattice Statistics". Physical Review Letters. American Physical Society (APS). 26 (14): 832–833. Bibcode:1971PhRvL..26..832B. doi:10.1103/physrevlett.26.832. ISSN 0031-9007.

[1]

[2]

[3]

Eight-vertex model

Contents

Description