Electromagnetic metasurface

Last updated
A liquid-tunable electromagnetic metasurface Metasurface (5941035620).jpg
A liquid-tunable electromagnetic metasurface

An electromagnetic metasurface refers to a kind of artificial sheet material with sub-wavelength thickness. Metasurfaces can be either structured or unstructured with subwavelength-scaled patterns in the horizontal dimensions. [1] [2] [3]

Contents

In electromagnetic theory, metasurfaces modulate the behaviors of electromagnetic waves through specific boundary conditions rather than constitutive parameters in three-dimensional (3D) space, which is commonly exploited in natural materials and metamaterials. Metasurfaces may also refer to the two-dimensional counterparts of metamaterials. [4] [5] There are also 2.5D metasurfaces that involve the third dimension as additional degree of freedom for tailoring their functionality. [6]

Definitions

Metasurfaces have been defined in several ways by researchers.

1, “An alternative approach that has gained increasing attention in recent years deals with one- and two-dimensional (1D and 2D) plasmonic arrays with subwavelength periodicity, also known as metasurfaces. Due to their negligible thickness compared to the wavelength of operation, metasurfaces can (near resonances of unit cell constituents) be considered as an interface of discontinuity enforcing an abrupt change in both the amplitude and phase of the impinging light”. [7]

2, “Our results can be understood using the concept of a metasurface, a periodic array of scattering elements whose dimensions and periods are small compared with the operating wavelength”. [8]

3, “Metasurfaces based on thin films”. A highly absorbing ultrathin film on a substrate can also be considered as a metasurface, with properties not occurring in natural materials. [3] Following this definition, the thin metallic films such as that in superlens are also the early type of metasurfaces. [9]

History

The research of electromagnetic metasurfaces has a long history. Early in 1902, Robert W. Wood found that the reflection spectra of subwavelength metallic grating had dark areas. This unusual phenomenon was named Wood's anomaly and led to the discovery of the surface plasmon polariton (SPP), [10] a particular electromagnetic wave excited at metal surfaces. Subsequently, another important phenomenon, the Levi-Civita relation, [11] was introduced, which states that a subwavelength-thick film can result in a dramatic change in electromagnetic boundary conditions.

Generally speaking, metasurfaces could include some traditional concepts in the microwave spectrum, such as frequency selective surfaces (FSS), impedance sheets, and even Ohmic sheets. In the microwave regime, the thickness of these metasurfaces can be much smaller than the wavelength of operation (for example, 1/1000 of the wavelength) since the skin depth could be minimal for highly conductive metals. Recently, some novel phenomena were demonstrated, such as ultra-broadband coherent perfect absorption. The results showed that a 0.3 nm thick film could absorb all electromagnetic waves across the RF, microwave, and terahertz frequencies. [12] [13] [14]

In optical applications, an anti-reflective coating could also be regarded as a simple metasurface, as first observed by Lord Rayleigh.

In recent years, several new metasurfaces have been developed, including plasmonic metasurfaces, [15] [4] [7] [16] [17] metasurfaces based on geometric phases, [18] [19] metasurfaces based on impedance sheets, [20] [21] and glide-symmetric metasurfaces. [22]

Applications

One of the most important applications of metasurfaces is to control a wavefront of electromagnetic waves by imparting local, gradient phase shifts to the incoming waves, which leads to a generalization of the ancient laws of reflection and refraction. [18] In this way, a metasurface can be used as a planar lens, [23] [24] illumination lens, [25] planar hologram, [26] vortex generator, [27] beam deflector, axicon and so on. [19] [28]

Besides the gradient metasurface lenses, metasurface-based superlenses offer another degree of control of the wavefront by using evanescent waves. With surface plasmons in the ultrathin metallic layers, perfect imaging and super-resolution lithography could be possible, which breaks the common assumption that all optical lens systems are limited by diffraction, a phenomenon called the diffraction limit. [29] [30]

Another promising application is in the field of stealth technology. A target's radar cross-section (RCS) has conventionally been reduced by either radiation-absorbent material (RAM) or by purpose shaping of the targets such that the scattered energy can be redirected away from the source. Unfortunately, RAMs have narrow frequency-band functionality, and purpose shaping limits the aerodynamic performance of the target. Metasurfaces have been synthesized that redirect scattered energy away from the source using either array theory [31] [32] [33] or the generalized Snell's law. [34] [35] This has led to aerodynamically favorable shapes for the targets with reduced RCS.

Metasurface can also be integrated with optical waveguides for controlling guided electromagnetic waves. [36] [37] Applications for meta-waveguides such as integrated waveguide mode converters, [37] structured-light generations, [38] [39] versatile multiplexers, [40] [41] and photonic neural networks [42] can be enabled.

In addition, metasurfaces are also applied in electromagnetic absorbers, polarization converters, and spectrum filters. Metasurface-empowered novel bioimaging and biosensing devices have also emerged and been reported recently. [43] [44] [45] [46] For many optically based bioimaging devices, their bulk footprint and heavy physical weight have limited their usage in clinical settings. [47] [48]

Simulation

To analyze such planar optical metasurfaces efficiently, prism-based algorithms allow for triangular prismatic space discretization, which is optimal for planar geometries. The prism-based algorithm has fewer elements than conventional tetrahedral methods, bringing higher computational efficiency. [49] A simulation toolkit has been released online, enabling users to efficiently analyze metasurfaces with customized pixel patterns. [50]

Optical characterization

Characterizing metasurfaces in the optical domain requires advanced imaging methods since the involved optical properties often include both phase and polarization properties. Recent works suggest that vectorial ptychography, a recently developed computational imaging method, appears very relevant. It combines the Jones matrix mapping with a microscopic lateral resolution, even on large specimens. [51]

Related Research Articles

<span class="mw-page-title-main">Photonic crystal</span> Periodic optical nanostructure that affects the motion of photons

A photonic crystal is an optical nanostructure in which the refractive index changes periodically. This affects the propagation of light in the same way that the structure of natural crystals gives rise to X-ray diffraction and that the atomic lattices of semiconductors affect their conductivity of electrons. Photonic crystals occur in nature in the form of structural coloration and animal reflectors, and, as artificially produced, promise to be useful in a range of applications.

<span class="mw-page-title-main">Metamaterial</span> Materials engineered to have properties that have not yet been found in nature

A metamaterial is any material engineered to have a property that is rarely observed in naturally occurring materials. They are made from assemblies of multiple elements fashioned from composite materials such as metals and plastics. These materials are usually arranged in repeating patterns, at scales that are smaller than the wavelengths of the phenomena they influence. Metamaterials derive their properties not from the properties of the base materials, but from their newly designed structures. Their precise shape, geometry, size, orientation and arrangement gives them their smart properties capable of manipulating electromagnetic waves: by blocking, absorbing, enhancing, or bending waves, to achieve benefits that go beyond what is possible with conventional materials.

<span class="mw-page-title-main">Optical vortex</span> Optical phenomenon

An optical vortex is a zero of an optical field; a point of zero intensity. The term is also used to describe a beam of light that has such a zero in it. The study of these phenomena is known as singular optics.

Nanophotonics or nano-optics is the study of the behavior of light on the nanometer scale, and of the interaction of nanometer-scale objects with light. It is a branch of optics, optical engineering, electrical engineering, and nanotechnology. It often involves dielectric structures such as nanoantennas, or metallic components, which can transport and focus light via surface plasmon polaritons.

<span class="mw-page-title-main">Extraordinary optical transmission</span>

Extraordinary optical transmission (EOT) is the phenomenon of greatly enhanced transmission of light through a subwavelength aperture in an otherwise opaque metallic film which has been patterned with a regularly repeating periodic structure. Generally when light of a certain wavelength falls on a subwavelength aperture, it is diffracted isotropically in all directions evenly, with minimal far-field transmission. This is the understanding from classical aperture theory as described by Bethe. In EOT however, the regularly repeating structure enables much higher transmission efficiency to occur, up to several orders of magnitude greater than that predicted by classical aperture theory. It was first described in 1998.

A spaser or plasmonic laser is a type of laser which aims to confine light at a subwavelength scale far below Rayleigh's diffraction limit of light, by storing some of the light energy in electron oscillations called surface plasmon polaritons. The phenomenon was first described by David J. Bergman and Mark Stockman in 2003. The word spaser is an acronym for "surface plasmon amplification by stimulated emission of radiation". The first such devices were announced in 2009 by three groups: a 44-nanometer-diameter nanoparticle with a gold core surrounded by a dyed silica gain medium created by researchers from Purdue, Norfolk State and Cornell universities, a nanowire on a silver screen by a Berkeley group, and a semiconductor layer of 90 nm surrounded by silver pumped electrically by groups at the Eindhoven University of Technology and at Arizona State University. While the Purdue-Norfolk State-Cornell team demonstrated the confined plasmonic mode, the Berkeley team and the Eindhoven-Arizona State team demonstrated lasing in the so-called plasmonic gap mode. In 2018, a team from Northwestern University demonstrated a tunable nanolaser that can preserve its high mode quality by exploiting hybrid quadrupole plasmons as an optical feedback mechanism.

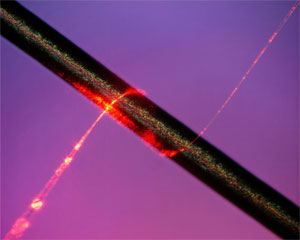
<span class="mw-page-title-main">Subwavelength-diameter optical fibre</span>

A subwavelength-diameter optical fibre is an optical fibre whose diameter is less than the wavelength of the light being propagated through it. An SDF usually consists of long thick parts at both ends, transition regions (tapers) where the fibre diameter gradually decreases down to the subwavelength value, and a subwavelength-diameter waist, which is the main acting part. Due to such a strong geometrical confinement, the guided electromagnetic field in an SDF is restricted to a single mode called fundamental.

<span class="mw-page-title-main">Terahertz metamaterial</span>

A terahertz metamaterial is a class of composite metamaterials designed to interact at terahertz (THz) frequencies. The terahertz frequency range used in materials research is usually defined as 0.1 to 10 THz.

<span class="mw-page-title-main">Photonic metamaterial</span> Type of electromagnetic metamaterial

A photonic metamaterial (PM), also known as an optical metamaterial, is a type of electromagnetic metamaterial, that interacts with light, covering terahertz (THz), infrared (IR) or visible wavelengths. The materials employ a periodic, cellular structure.

A metamaterial absorber is a type of metamaterial intended to efficiently absorb electromagnetic radiation such as light. Furthermore, metamaterials are an advance in materials science. Hence, those metamaterials that are designed to be absorbers offer benefits over conventional absorbers such as further miniaturization, wider adaptability, and increased effectiveness. Intended applications for the metamaterial absorber include emitters, photodetectors, sensors, spatial light modulators, infrared camouflage, wireless communication, and use in solar photovoltaics and thermophotovoltaics.

<span class="mw-page-title-main">Coherent perfect absorber</span>

A coherent perfect absorber (CPA), or anti-laser, is a device which absorbs coherent waves, such as coherent light waves, and converts them into some form of internal energy, e.g. heat or electrical energy. It is the time-reversed counterpart of a laser. Coherent perfect absorption allows control of waves with waves without a nonlinear medium. The concept was first published in the July 26, 2010, issue of Physical Review Letters, by a team at Yale University led by theorist A. Douglas Stone and experimental physicist Hui W. Cao. In the September 9, 2010, issue of Physical Review A, Stefano Longhi of Polytechnic University of Milan showed how to combine a laser and an anti-laser in a single device. In February 2011 the team at Yale built the first working anti-laser. It is a two-channel CPA device which absorbs two beams from the same laser, but only when the beams have the correct phases and amplitudes. The initial device absorbed 99.4 percent of all incoming light, but the team behind the invention believe it will be possible to achieve 99.999 percent. Originally implemented as a Fabry-Pérot cavity that is many wavelengths thick, the optical CPA operates at specific optical frequencies. In January 2012, thin-film CPA has been proposed by utilizing the achromatic dispersion of metal-like materials, exhibiting the unparalleled bandwidth and thin profile advantages. Shortly after, CPA was observed in various thin film materials, including photonic metamaterial, multi-layer graphene, single and multiple layers of chromium, as well as microwave metamaterial.

A flat lens is a lens whose flat shape allows it to provide distortion-free imaging, potentially with arbitrarily-large apertures. The term is also used to refer to other lenses that provide a negative index of refraction. Flat lenses require a refractive index close to −1 over a broad angular range. In recent years, flat lenses based on metasurfaces were also demonstrated.

A plasmonic metamaterial is a metamaterial that uses surface plasmons to achieve optical properties not seen in nature. Plasmons are produced from the interaction of light with metal-dielectric materials. Under specific conditions, the incident light couples with the surface plasmons to create self-sustaining, propagating electromagnetic waves known as surface plasmon polaritons (SPPs). Once launched, the SPPs ripple along the metal-dielectric interface. Compared with the incident light, the SPPs can be much shorter in wavelength.

Photonic molecules are a form of matter in which photons bind together to form "molecules". They were first predicted in 2007. Photonic molecules are formed when individual (massless) photons "interact with each other so strongly that they act as though they have mass". In an alternative definition, photons confined to two or more coupled optical cavities also reproduce the physics of interacting atomic energy levels, and have been termed as photonic molecules.

In physics, a high contrast grating is a single layer near-wavelength grating physical structure where the grating material has a large contrast in index of refraction with its surroundings. The term near-wavelength refers to the grating period, which has a value between one optical wavelength in the grating material and that in its surrounding materials.

<span class="mw-page-title-main">Plasmonics</span>

Plasmonics or nanoplasmonics refers to the generation, detection, and manipulation of signals at optical frequencies along metal-dielectric interfaces in the nanometer scale. Inspired by photonics, plasmonics follows the trend of miniaturizing optical devices, and finds applications in sensing, microscopy, optical communications, and bio-photonics.

Photonic topological insulators are artificial electromagnetic materials that support topologically non-trivial, unidirectional states of light. Photonic topological phases are classical electromagnetic wave analogues of electronic topological phases studied in condensed matter physics. Similar to their electronic counterparts, they, can provide robust unidirectional channels for light propagation.

Spoof surface plasmons, also known as spoof surface plasmon polaritons and designer surface plasmons, are surface electromagnetic waves in microwave and terahertz regimes that propagate along planar interfaces with sign-changing permittivities. Spoof surface plasmons are a type of surface plasmon polariton, which ordinarily propagate along metal and dielectric interfaces in infrared and visible frequencies. Since surface plasmon polaritons cannot exist naturally in microwave and terahertz frequencies due to dispersion properties of metals, spoof surface plasmons necessitate the use of artificially-engineered metamaterials.

Milton Kerker was an American physical chemist and former professor at department of chemistry at Clarkson University. He is best known for his work on aerosol, interface and colloid science, as well as for pioneering surface-enhanced Raman spectroscopy. Kerker effect in optics is named after him.

In photonics, a meta-waveguide is a physical structures that guides electromagnetic waves with engineered functional subwavelength structures. Meta-waveguides are the result of combining the fields of metamaterials and metasurfaces into integrated optics. The design of the subwavelength architecture allows exotic waveguiding phenomena to be explored.

References

  1. ↑ Bomzon, Ze’ev; Kleiner, Vladimir; Hasman, Erez (2001-09-15). "Pancharatnam–Berry phase in space-variant polarization-state manipulations with subwavelength gratings". Optics Letters. 26 (18): 1424–1426. Bibcode:2001OptL...26.1424B. doi:10.1364/OL.26.001424. ISSN   1539-4794. PMID   18049626.
  2. ↑ Bomzon, Ze’ev; Biener, Gabriel; Kleiner, Vladimir; Hasman, Erez (2002-07-01). "Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings". Optics Letters. 27 (13): 1141–1143. Bibcode:2002OptL...27.1141B. doi:10.1364/OL.27.001141. ISSN   1539-4794. PMID   18026387.
  3. 1 2 Yu, Nanfang; Capasso, Federico (2014). "Flat optics with designer metasurfaces". Nat. Mater. 13 (2): 139–150. Bibcode:2014NatMa..13..139Y. doi:10.1038/nmat3839. PMID   24452357.
  4. 1 2 Zeng, S.; et al. (2015). "Graphene-gold metasurface architectures for ultrasensitive plasmonic biosensing". Advanced Materials. 27 (40): 6163–6169. Bibcode:2015AdM....27.6163Z. doi:10.1002/adma.201501754. hdl: 20.500.12210/45908 . PMID   26349431. S2CID   205261271.
  5. ↑ Quevedo-Teruel, O.; et al. (2019). "Roadmap on metasurfaces". Journal of Optics. 21 (7): 073002. Bibcode:2019JOpt...21g3002Q. doi: 10.1088/2040-8986/ab161d . hdl: 10016/33235 . S2CID   198449951.
  6. ↑ Solomonov, A.I.; et al. (2023). "2.5D switchable metasurfaces". Optics & Laser Technology. 161: 109122. Bibcode:2023OptLT.16109122S. doi:10.1016/j.optlastec.2023.109122. S2CID   255887266.
  7. 1 2 Pors, Anders; Bozhevolnyi, Sergey I. (2013). "Plasmonic metasurfaces for efficient phase control in reflection". Optics Express. 21 (22): 27438–27451. Bibcode:2013OExpr..2127438P. doi: 10.1364/OE.21.027438 . PMID   24216965.
  8. ↑ Li, Ping-Chun; Zhao, Yang; Alu, Andrea; Yu, Edward T. (2011). "Experimental realization and modeling of a subwavelength frequency-selective plasmonic metasurface". Appl. Phys. Lett. 99 (3): 221106. Bibcode:2011ApPhL..99c1106B. doi:10.1063/1.3614557.
  9. ↑ Pendry, J. B. (2000). "Negative Refraction Makes a Perfect Lens" (PDF). Physical Review Letters . 85 (18): 3966–9. Bibcode:2000PhRvL..85.3966P. doi:10.1103/PhysRevLett.85.3966. PMID   11041972. S2CID   25803316. Archived from the original (PDF) on 2016-04-18. Retrieved 2015-05-21.
  10. ↑ Wood, R. W. (1902). "On a remarkable case of uneven distribution of light in a diffraction grating spectrum". Proc. Phys. Soc. Lond. 18 (1): 269–275. Bibcode:1902PPSL...18..269W. doi:10.1088/1478-7814/18/1/325.
  11. ↑ Senior, T. (1981). "Approximate boundary conditions". IEEE Trans. Antennas Propag. 29 (5): 826–829. Bibcode:1981ITAP...29..826S. doi:10.1109/tap.1981.1142657. hdl: 2027.42/20954 .
  12. ↑ Pu, M.; et al. (17 January 2012). "Ultrathin broadband nearly perfect absorber with symmetrical coherent illumination". Optics Express. 20 (3): 2246–2254. Bibcode:2012OExpr..20.2246P. doi: 10.1364/oe.20.002246 . PMID   22330464.
  13. ↑ Li, S.; et al. (2015). "Broadband Perfect Absorption of Ultrathin Conductive Films with Coherent Illumination: Super Performance of Electromagnetic Absorption". Physical Review B. 91 (22): 220301. arXiv: 1406.1847 . Bibcode:2015PhRvB..91v0301L. doi:10.1103/PhysRevB.91.220301. S2CID   118609773.
  14. ↑ Taghvaee, H.R.; et al. (2017). "Circuit modeling of graphene absorber in terahertz band". Optics Communications. 383: 11–16. Bibcode:2017OptCo.383...11T. doi:10.1016/j.optcom.2016.08.059.
  15. ↑ Ni, X.; Emani, N. K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. (2012). "Broadband light bending with plasmonic nanoantennas". Science. 335 (6067): 427. Bibcode:2012Sci...335..427N. doi: 10.1126/science.1214686 . PMID   22194414. S2CID   18790738.
  16. ↑ Verslegers, Lieven; Fan, Shanhui (2009). "Planar Lenses Based on Nanoscale Slit Arrays in a Metallic Film". Nano Lett. 9 (1): 235–238. Bibcode:2009NanoL...9..235V. doi:10.1021/nl802830y. PMID   19053795. S2CID   28741710.
  17. ↑ Kildishev, A. V.; Boltasseva, A.; Shalaev, V. M. (2013). "Planar photonics with metasurfaces". Science. 339 (6125): 1232009. doi:10.1126/science.1232009. PMID   23493714. S2CID   33896271.
  18. 1 2 Yu, Nanfang; Genevet, Patrice; Mikhail Kats; Aieta, Francesco; Tetienne, Jean-Philippe; Capasso, Federico; Gaburro, Zeno (2011). "Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction". Science. 334 (6054): 333–337. Bibcode:2011Sci...334..333Y. doi: 10.1126/science.1210713 . PMID   21885733. S2CID   10156200.
  19. 1 2 Lin, Dianmin; Fan, Pengyu; Hasman, Erez; Brongersma, Mark L. (2014). "Dielectric gradient metasurface optical elements". Science. 345 (6194): 298–302. Bibcode:2014Sci...345..298L. doi:10.1126/science.1253213. PMID   25035488. S2CID   29708554.
  20. ↑ Pfeiffer, Carl; Grbic, Anthony (2013). "Metamaterial Huygens' Surfaces: Tailoring Wave Fronts with Reflectionless Sheets". Phys. Rev. Lett. 110 (2): 197401. arXiv: 1206.0852 . Bibcode:2013PhRvL.110b7401W. doi:10.1103/PhysRevLett.110.027401. PMID   23383937. S2CID   118458038.
  21. ↑ Felbacq, Didier (2015). "Impedance operator description of a metasurface". Mathematical Problems in Engineering. 2015: 473079. arXiv: 1507.07736 . doi: 10.1155/2015/473079 .
  22. ↑ Quevedo-Teruel, Oscar; et al. (2021). "On the benefits of glide symmetries for microwave devices". IEEE Journal of Microwaves. 1: 457–469. doi: 10.1109/JMW.2020.3033847 . S2CID   231619012.
  23. ↑ Aieta, Francesco; Genevet, Patrice; Kats, Mikhail; Yu, Nanfang; Blanchard, Romain; Gaburro, Zeno; Capasso, Federico (2012). "Aberration-free ultra-thin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces". Nano Letters. 12 (9): 4932–6. arXiv: 1207.2194 . Bibcode:2012NanoL..12.4932A. doi:10.1021/nl302516v. PMID   22894542. S2CID   5412108.
  24. ↑ Ni, X.; Ishii, S.; Kildishev, A.V.; Shalaev, V.M. (2013). "Ultra-thin, planar, Babinet-inverted plasmonic metalenses" (PDF). Light: Science & Applications. 2 (4): e72. Bibcode:2013LSA.....2E..72N. doi:10.1038/lsa.2013.28. S2CID   8927737.
  25. ↑ I. Moreno, M. Avendaño-Alejo, and C. P. Castañeda-Almanza, "Nonimaging metaoptics," Opt. Lett. 45, 2744-2747 (2020). https://doi.org/10.1364/OL.391357
  26. ↑ Ni, X.; Kildishev, A.V.; Shalaev, V.M. (2013). "Metasurface holograms for visible light" (PDF). Nature Communications. 4: 1–6. Bibcode:2013NatCo...4.2807N. doi:10.1038/ncomms3807. S2CID   5550551.
  27. ↑ Genevet, Patrice; Yu, Nanfang; Aieta, Francesco; Lin, Jiao; Kats, Mikhail; Blanchard, Romain; Scully, Marlan; Gaburro, Zeno; Capasso, Federico (2012). "Ultra-thin plasmonic optical vortex plate based on phase discontinuities". Applied Physics Letters. 100 (1): 013101. Bibcode:2012ApPhL.100a3101G. doi:10.1063/1.3673334.
  28. ↑ Xu, T.; et al. (2008). "Plasmonic deflector". Opt. Express. 16 (7): 4753–4759. Bibcode:2008OExpr..16.4753X. doi: 10.1364/oe.16.004753 . PMID   18542573.
  29. ↑ Luo, Xiangang; Ishihara, Teruya (2004). "Surface plasmon resonant interference nanolithography technique". Appl. Phys. Lett. 84 (23): 4780. Bibcode:2004ApPhL..84.4780L. doi:10.1063/1.1760221.
  30. ↑ Fang, Nicholas; Lee, Hyesog; Sun, Cheng; Zhang, Xiang (2005). "Sub-Diffraction-Limited Optical Imaging with a Silver Superlens". Science. 308 (5721): 534–7. Bibcode:2005Sci...308..534F. doi:10.1126/science.1108759. PMID   15845849. S2CID   1085807.
  31. ↑ Modi, A. Y.; Alyahya, M. A.; Balanis, C. A.; Birtcher, C. R. (2019). "Metasurface-Based Method for Broadband RCS Reduction of Dihedral Corner Reflectors with Multiple Bounces". IEEE Transactions on Antennas and Propagation. 68 (3): 1. doi:10.1109/TAP.2019.2940494. S2CID   212649480.
  32. ↑ Modi, A. Y.; Balanis, C. A.; Birtcher, C. R.; Shaman, H. (2019). "New Class of RCS-Reduction Metasurfaces Based on Scattering Cancellation Using Array Theory". IEEE Transactions on Antennas and Propagation. 67 (1): 298–308. Bibcode:2019ITAP...67..298M. doi:10.1109/TAP.2018.2878641. S2CID   58670543.
  33. ↑ Modi, A. Y.; Balanis, C. A.; Birtcher, C. R.; Shaman, H. (2017). "Novel Design of Ultrabroadband Radar Cross Section Reduction Surfaces using Artificial Magnetic Conductors". IEEE Transactions on Antennas and Propagation. 65 (10): 5406–5417. Bibcode:2017ITAP...65.5406M. doi:10.1109/TAP.2017.2734069. S2CID   20724998.
  34. ↑ Li, Yongfeng; Zhang, Jieqiu; Qu, Shaobo; Wang, Jiafu; Chen, Hongya; Xu, Zhuo; Zhang, Anxue (2014). "Wideband radar cross section reduction using two-dimensional phase gradient metasurfaces". Applied Physics Letters. 104 (22): 221110. Bibcode:2014ApPhL.104v1110L. doi:10.1063/1.4881935.
  35. ↑ Yu, Nanfang; Genevet, Patrice; Kats, Mikhail A.; Aieta, Francesco; Tetienne, Jean-Philippe; Capasso, Federico; Gaburro, Zeno (October 2011). "Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction". Science. 334 (6054): 333–337. Bibcode:2011Sci...334..333Y. doi: 10.1126/science.1210713 . PMID   21885733. S2CID   10156200.
  36. ↑ Meng, Yuan; Chen, Yizhen; Lu, Longhui; Ding, Yimin; Cusano, Andrea; Fan, Jonathan A.; Hu, Qiaomu; Wang, Kaiyuan; Xie, Zhenwei; Liu, Zhoutian; Yang, Yuanmu (2021-11-22). "Optical meta-waveguides for integrated photonics and beyond". Light: Science & Applications. 10 (1): 235. Bibcode:2021LSA....10..235M. doi:10.1038/s41377-021-00655-x. ISSN   2047-7538. PMC   8608813 . PMID   34811345.
  37. 1 2 Li, Zhaoyi; Kim, Myoung-Hwan; Wang, Cheng; Han, Zhaohong; Shrestha, Sajan; Overvig, Adam Christopher; Lu, Ming; Stein, Aaron; Agarwal, Anuradha Murthy; Lončar, Marko; Yu, Nanfang (July 2017). "Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces". Nature Nanotechnology. 12 (7): 675–683. Bibcode:2017NatNa..12..675L. doi:10.1038/nnano.2017.50. ISSN   1748-3395. OSTI   1412777. PMID   28416817.
  38. ↑ Guo, Xuexue; Ding, Yimin; Chen, Xi; Duan, Yao; Ni, Xingjie (2020-07-17). "Molding free-space light with guided wave–driven metasurfaces". Science Advances. 6 (29): eabb4142. arXiv: 2001.03001 . Bibcode:2020SciA....6.4142G. doi:10.1126/sciadv.abb4142. ISSN   2375-2548. PMC   7439608 . PMID   32832643.
  39. ↑ He, Tiantian; Meng, Yuan; Liu, Zhoutian; Hu, Futai; Wang, Rui; Li, Dan; Yan, Ping; Liu, Qiang; Gong, Mali; Xiao, Qirong (2021-11-22). "Guided mode meta-optics: metasurface-dressed waveguides for arbitrary mode couplers and on-chip OAM emitters with a configurable topological charge". Optics Express. 29 (24): 39406–39418. Bibcode:2021OExpr..2939406H. doi: 10.1364/OE.443186 . ISSN   1094-4087. PMID   34809306. S2CID   243813207.
  40. ↑ Cheben, Pavel; Halir, Robert; Schmid, Jens H.; Atwater, Harry A.; Smith, David R. (August 2018). "Subwavelength integrated photonics". Nature. 560 (7720): 565–572. Bibcode:2018Natur.560..565C. doi:10.1038/s41586-018-0421-7. ISSN   1476-4687. PMID   30158604. S2CID   52117964.
  41. ↑ Meng, Yuan; Liu, Zhoutian; Xie, Zhenwei; Wang, Ride; Qi, Tiancheng; Hu, Futai; Kim, Hyunseok; Xiao, Qirong; Fu, Xing; Wu, Qiang; Bae, Sang-Hoon; Gong, Mali; Yuan, Xiaocong (2020-04-01). "Versatile on-chip light coupling and (de)multiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface". Photonics Research. 8 (4): 564. doi:10.1364/PRJ.384449. ISSN   2327-9125. S2CID   213576669.
  42. ↑ Wu, Changming; Yu, Heshan; Lee, Seokhyeong; Peng, Ruoming; Takeuchi, Ichiro; Li, Mo (2021-01-04). "Programmable phase-change metasurfaces on waveguides for multimode photonic convolutional neural network". Nature Communications. 12 (1): 96. arXiv: 2004.10651 . Bibcode:2021NatCo..12...96W. doi:10.1038/s41467-020-20365-z. ISSN   2041-1723. PMC   7782756 . PMID   33398011.
  43. ↑ A. Arbabi (2016). "Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations". Nature Communications. 7: 13682–89. arXiv: 1604.06160 . Bibcode:2016NatCo...713682A. doi:10.1038/ncomms13682. PMC   5133709 . PMID   27892454.
  44. ↑ W. Chen (2018). "A broadband achromatic metalens for focusing and imaging in the visible". Nature Nanotechnology. 13 (3): 220–226. Bibcode:2018NatNa..13..220C. doi:10.1038/s41565-017-0034-6. PMID   29292382. S2CID   205567341.
  45. ↑ S. Zhang (2020). "Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective". Nanophotonics. 10 (1): 259–293. Bibcode:2020Nanop..10..373Z. doi: 10.1515/nanoph-2020-0373 . hdl: 10023/20902 . S2CID   225279574.
  46. ↑ L. Jiang (2017). "Multifunctional hyperbolic nanogroove metasurface for submolecular detection". Small. 13 (30): 1700600–10. doi:10.1002/smll.201700600. PMID   28597602.
  47. ↑ M. Beruete (2019). "Terahertz sensing based on metasurfaces". Advanced Optical Materials. 8 (3): 1900721–28. doi:10.1002/adom.201900721. S2CID   199649103.
  48. ↑ R. Ahmed (2020). "Tunable Fano‐resonant metasurfaces on a disposable plastic‐template for multimodal and multiplex biosensing". Advanced Materials. 32 (19): 1907160–78. Bibcode:2020AdM....3207160A. doi:10.1002/adma.201907160. hdl:11693/75646. PMC   8713081 . PMID   32201997.
  49. ↑ Mai, Wending; Campbell, Sawyer D.; Whiting, Eric B.; Kang, Lei; Werner, Pingjuan L.; Chen, Yifan; Werner, Douglas H. (2020-10-01). "Prismatic discontinuous Galerkin time domain method with an integrated generalized dispersion model for efficient optical metasurface analysis". Optical Materials Express. 10 (10): 2542–2559. Bibcode:2020OMExp..10.2542M. doi: 10.1364/OME.399414 . ISSN   2159-3930.
  50. ↑ Mai, Wending; Werner, Douglas (2020). "prism-DGTD with GDM to analyze pixelized metasurfaces". doi:10.17605/OSF.IO/2NA4F.{{cite journal}}: Cite journal requires |journal= (help)
  51. ↑ Song, Qinghua; Baroni, Arthur; Sawant, Rajath; Ni, Peinan; Brandli, Virginie; Chenot, Sébastien; Vézian, Stéphane; Damilano, Benjamin; de Mierry, Philippe; Khadir, Samira; Ferrand, Patrick (December 2020). "Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces". Nature Communications. 11 (1): 2651. Bibcode:2020NatCo..11.2651S. doi:10.1038/s41467-020-16437-9. ISSN   2041-1723. PMC   7253437 . PMID   32461637.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.