
Entropy is a scientific concept that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication.

In thermodynamics, enthalpy, is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work that was done against constant external pressure to establish the system's physical dimensions from to some final volume , i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; bond, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it.

In thermodynamics, the specific heat capacity of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity or as the specific heat. Informally, it is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−1⋅K−1.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.
In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the redox reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.

The second law of thermodynamics is a physical law based on universal empirical observation concerning heat and energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter. Another statement is: "Not all heat can be converted into work in a cyclic process."

The third law of thermodynamics states that the entropy of a closed system at thermodynamic equilibrium approaches a constant value when its temperature approaches absolute zero. This constant value cannot depend on any other parameters characterizing the system, such as pressure or applied magnetic field. At absolute zero the system must be in a state with the minimum possible energy.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.

The internal energy of a thermodynamic system is the energy contained within it, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, i.e., the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. The internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics.

An isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic. Thermodynamic processes are named based on the effect they would have on the system. Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such.

In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature T of a system remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an adiabatic process is where a system exchanges no heat with its surroundings (Q = 0).

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.
The Clausius–Clapeyron relation, in chemical thermodynamics, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. It's named after Rudolf Clausius and Benoît Paul Émile Clapeyron. However, this relation was in fact originally derived by Sadi Carnot in his Reflections on the Motive Power of Fire, which was published in 1824 but largely ignored until it was rediscovered by Clausius, Clapeyron, and Lord Kelvin decades later. Kelvin said of Carnot's argument that "nothing in the whole range of Natural Philosophy is more remarkable than the establishment of general laws by such a process of reasoning."
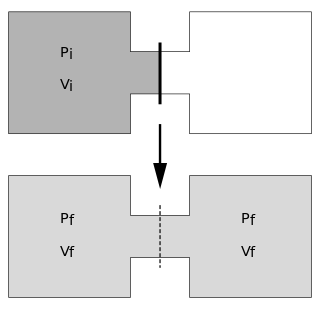
The Joule expansion is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container, with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container.
The Van 't Hoff equation relates the change in the equilibrium constant, Keq, of a chemical reaction to the change in temperature, T, given the standard enthalpy change, ΔrH⊖, for the process. The subscript means "reaction" and the superscript means "standard". It was proposed by Dutch chemist Jacobus Henricus van 't Hoff in 1884 in his book Études de Dynamique chimique.
In classical thermodynamics, entropy is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-19th century to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy. The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.

In thermodynamics, entropy is a numerical quantity that shows that many physical processes can go in only one direction in time. For example, cream and coffee can be mixed together, but cannot be "unmixed"; a piece of wood can be burned, but cannot be "unburned". The word 'entropy' has entered popular usage to refer a lack of order or predictability, or of a gradual decline into disorder. A more physical interpretation of thermodynamic entropy refers to spread of energy or matter, or to extent and diversity of microscopic motion.
In astrophysics, what is referred to as "entropy" is actually the adiabatic constant derived as follows.
The vaporizing droplet problem is a challenging issue in fluid dynamics. It is part of many engineering situations involving the transport and computation of sprays: fuel injection, spray painting, aerosol spray, flashing releases… In most of these engineering situations there is a relative motion between the droplet and the surrounding gas. The gas flow over the droplet has many features of the gas flow over a rigid sphere: pressure gradient, viscous boundary layer, wake. In addition to these common flow features one can also mention the internal liquid circulation phenomenon driven by surface-shear forces and the boundary layer blowing effect.
















































































