In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.

In mathematics, a metric space is a set together with a notion of distance between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry.

In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization of the intuitive notion of "length" in the physical world. If is a vector space over , where is a field equal to or to , then a norm on is a map , typically denoted by , satisfying the following four axioms:
- Non-negativity: for every ,.
- Positive definiteness: for every , if and only if is the zero vector.
- Absolute homogeneity: for every and ,
- Triangle inequality: for every and ,

In mathematics and physics, a vector space is a set whose elements, often called vectors, may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. Real vector space and complex vector space are kinds of vector spaces based on different kinds of scalars: real coordinate space or complex coordinate space.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.

In mathematics, a ball is the solid figure bounded by a sphere; it is also called a solid sphere. It may be a closed ball or an open ball.
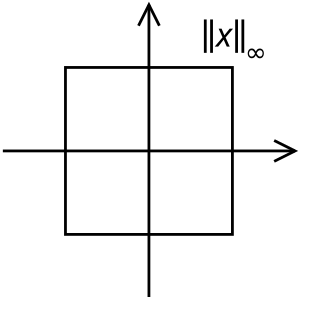
In mathematical analysis, the uniform norm assigns to real- or complex-valued bounded functions defined on a set the non-negative number

Taxicab geometry or Manhattan geometry is geometry where the familiar Euclidean distance is ignored, and the distance between two points is instead defined to be the sum of the absolute differences of their respective Cartesian coordinates, a distance function called the taxicab distance, Manhattan distance, or city block distance. The name refers to the island of Manhattan, or generically any planned city with a rectangular grid of streets, in which a taxicab can only travel along grid directions. In taxicab geometry, the distance between any two points equals the length of their shortest grid path. This different definition of distance also leads to a different definition of the length of a curve, for which a line segment between any two points has the same length as a grid path between those points rather than its Euclidean length.
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude of the vector. This norm can be defined as the square root of the inner product of a vector with itself.

In mathematics, the real coordinate space or real coordinate n-space, of dimension n, denoted Rn or , is the set of the n-tuples of real numbers, that is the set of all sequences of n real numbers. Special cases are called the real lineR1, the real coordinate planeR2, and the real coordinate three-dimensional spaceR3. With component-wise addition and scalar multiplication, it is a real vector space, and its elements are called coordinate vectors.
In mathematics, Chebyshev distance, maximum metric, or L∞ metric is a metric defined on a real coordinate space where the distance between two points is the greatest of their differences along any coordinate dimension. It is named after Pafnuty Chebyshev.

In Euclidean geometry, Ptolemy's inequality relates the six distances determined by four points in the plane or in a higher-dimensional space. It states that, for any four points A, B, C, and D, the following inequality holds:
In mathematics, Dvoretzky's theorem is an important structural theorem about normed vector spaces proved by Aryeh Dvoretzky in the early 1960s, answering a question of Alexander Grothendieck. In essence, it says that every sufficiently high-dimensional normed vector space will have low-dimensional subspaces that are approximately Euclidean. Equivalently, every high-dimensional bounded symmetric convex set has low-dimensional sections that are approximately ellipsoids.
In functional analysis, the dual norm is a measure of size for a continuous linear function defined on a normed vector space.
In the mathematical study of functional analysis, the Banach–Mazur distance is a way to define a distance on the set of -dimensional normed spaces. With this distance, the set of isometry classes of -dimensional normed spaces becomes a compact metric space, called the Banach–Mazur compactum.

The Minkowski distance or Minkowski metric is a metric in a normed vector space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance. It is named after the German mathematician Hermann Minkowski.

In mathematics, Hilbert spaces allow the methods of linear algebra and calculus to be generalized from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that induces a distance function for which the space is a complete metric space.
In mathematics, a unit sphere is a sphere of unit radius: the set of points at Euclidean distance 1 from some center point in three-dimensional space. More generally, the unit -sphere is an -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the plane. An (open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center.
In geometry, the distance set of a collection of points is the set of distances between distinct pairs of points. Thus, it can be seen as the generalization of a difference set, the set of distances in collections of numbers.







































