Fermat's spiral

Last updated October 16, 2023

Fermat's spiral, both branches Spiral-fermat-2.svg — Fermat's spiral, both branches

A Fermat's spiral or parabolic spiral is a plane curve with the property that the area between any two consecutive full turns around the spiral is invariant. As a result, the distance between turns grows in inverse proportion to their distance from the spiral center, contrasting with the Archimedean spiral (for which this distance is invariant) and the logarithmic spiral (for which the distance between turns is proportional to the distance from the center). Fermat spirals are named after Pierre de Fermat.^[1]

Coordinate representation

Polar

The representation of the Fermat spiral in polar coordinates $(r, φ)$ is given by the equation

r=\pm a{\sqrt {\varphi }}

for $φ \geq 0$ .

The two choices of sign give the two branches of the spiral, which meet smoothly at the origin. If the same variables were reinterpreted as Cartesian coordinates, this would be the equation of a parabola with horizontal axis, which again has two branches above and below the axis, meeting at the origin.

Cartesian

The Fermat spiral with polar equation

r=\pm a{\sqrt {\varphi }}

can be converted to the Cartesian coordinates $(x, y)$ by using the standard conversion formulas $x = r cos φ$ and $y = r sin φ$ . Using the polar equation for the spiral to eliminate $r$ from these conversions produces parametric equations for one branch of the curve:

{\begin{cases}x(\varphi )=+a{\sqrt {\varphi }}\cos(\varphi )\\y(\varphi )=+a{\sqrt {\varphi }}\sin(\varphi )\end{cases}}

and the second one

{\begin{cases}x(\varphi )=-a{\sqrt {\varphi }}\cos(\varphi )\\y(\varphi )=-a{\sqrt {\varphi }}\sin(\varphi )\end{cases}}

They generate the points of branches of the curve as the parameter $φ$ ranges over the positive real numbers.

For any $(x, y)$ generated in this way, dividing $x$ by $y$ cancels the $a \sqrt φ$ parts of the parametric equations, leaving the simpler equation $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}x/y = cot φ$ . From this equation, substituting $φ$ by $φ = r 2 / a 2$ (a rearranged form of the polar equation for the spiral) and then substituting $r$ by $r = \sqrt x 2 + y 2$ (the conversion from Cartesian to polar) leaves an equation for the Fermat spiral in terms of only $x$ and $y$ :

{\frac {x}{y}}=\cot \left({\frac {x^{2}+y^{2}}{a^{2}}}\right).

Because the sign of $a$ is lost when it is squared, this equation covers both branches of the curve.

Geometric properties

A Fermat's spiral divides the plane into two connected and congruent regions (diagram: black and white) Fermat-spiral-components.svg — A Fermat's spiral divides the plane into two connected and congruent regions (diagram: black and white)

Division of the plane

A complete Fermat's spiral (both branches) is a smooth double point free curve, in contrast with the Archimedean and hyperbolic spiral. Like a line or circle or parabola, it divides the plane into two connected regions.

Polar slope

From vector calculus in polar coordinates one gets the formula

\tan \alpha ={\frac {r'}{r}}

for the polar slope and its angle $α$ between the tangent of a curve and the corresponding polar circle (see diagram).

For Fermat's spiral $r = a \sqrt φ$ one gets

\tan \alpha ={\frac {1}{2\varphi }}.

Hence the slope angle is monotonely decreasing.

Curvature

From the formula

\kappa ={\frac {r^{2}+2(r')^{2}-r\,r''}{\left(r^{2}+(r')^{2}\right)^{\frac {3}{2}}}}

for the curvature of a curve with polar equation $r = r (φ)$ and its derivatives

{\begin{aligned}r'&={\frac {a}{2{\sqrt {\varphi }}}}={\frac {a^{2}}{2r}}\\r''&=-{\frac {a}{4{\sqrt {\varphi }}^{3}}}=-{\frac {a^{4}}{4r^{3}}}\end{aligned}}

one gets the curvature of a Fermat's spiral:

\kappa (r)={\frac {2r\left(4r^{4}+3a^{4}\right)}{\left(4r^{4}+a^{4}\right)^{\frac {3}{2}}}}.

At the origin the curvature is 0. Hence the complete curve has at the origin an inflection point and the $x$ -axis is its tangent there.

Area between arcs

The area of a sector of Fermat's spiral between two points $(r (φ 1), φ 1)$ and $(r (φ 2), φ 2)$ is

{\begin{aligned}{\underline {A}}&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi \,d\varphi \\&={\frac {a^{2}}{4}}\left(\varphi _{2}^{2}-\varphi _{1}^{2}\right)\\&={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}\right)\left(\varphi _{2}-\varphi _{1}\right).\end{aligned}}

Fermat's spiral: area between neighbored arcs Spiral-fermat-area.svg — Fermat's spiral: area between neighbored arcs

After raising both angles by $2 π$ one gets

{\overline {A}}={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}+4\pi \right)\left(\varphi _{2}-\varphi _{1}\right)={\underline {A}}+a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right).

Hence the area $A$ of the region between two neighboring arcs is

A=a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right).

$A$ only depends on the difference of the two angles, not on the angles themselves.

For the example shown in the diagram, all neighboring stripes have the same area: $A 1 = A 2 = A 3$ .

This property is used in electrical engineering for the construction of variable capacitors.^[2]

Special case due to Fermat

In 1636, Fermat wrote a letter ^[3] to Marin Mersenne which contains the following special case:

Let $φ 1 = 0, φ 2 = 2 π$ ; then the area of the black region (see diagram) is $A 0 = a 2 π 2$ , which is half of the area of the circle $K 0$ with radius $r (2 π)$ . The regions between neighboring curves (white, blue, yellow) have the same area $A = 2 a 2 π 2$ . Hence:

The area between two arcs of the spiral after a full turn equals the area of the circle $K 0$ .

Arc length

The length of the arc of Fermat's spiral between two points $(r (φ i), φ i)$ can be calculated by the integral:

{\begin{aligned}L&=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,d\varphi \\&={\frac {a}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {1}{\varphi }}+4\varphi }}\,d\varphi .\end{aligned}}

This integral leads to an elliptical integral, which can be solved numerically.

The arc length of the positive branch of the Fermat's spiral from the origin can also be defined by hypergeometric functions $2 F 1 (a, b; c; z)$ and the incomplete beta function $B(z; a, b)$ :^[4]

{\begin{aligned}L&=a\cdot {\sqrt {\varphi }}\cdot \operatorname {_{2}F_{1}} \left(-{\tfrac {1}{2}},\,{\tfrac {1}{4}};\,{\tfrac {5}{4}};\,-4\cdot \varphi ^{2}\right)\\&=a\cdot {\frac {1-i}{8}}\cdot \operatorname {B} \left(-4\cdot \varphi ^{2};\,{\tfrac {1}{4}},\,{\tfrac {3}{2}}\right)\\\end{aligned}}

The inversion of Fermat's spiral (green) is a lituus (blue) Invers-fermats-lits.svg — The inversion of Fermat's spiral (green) is a lituus (blue)

Circle inversion

The inversion at the unit circle has in polar coordinates the simple description $(r, φ) \mapsto (1 / r, φ)$ .

The image of Fermat's spiral $r = a \sqrt φ$ under the inversion at the unit circle is a lituus spiral with polar equation $r={\frac {1}{a{\sqrt {\varphi }}}}.$ When $φ = 1 / a 2$ , both curves intersect at a fixed point on the unit circle.
The tangent ( $x$ -axis) at the inflection point (origin) of Fermat's spiral is mapped onto itself and is the asymptotic line of the lituus spiral.

The golden ratio and the golden angle

In disc phyllotaxis, as in the sunflower and daisy, the mesh of spirals occurs in Fibonacci numbers because divergence (angle of succession in a single spiral arrangement) approaches the golden ratio. The shape of the spirals depends on the growth of the elements generated sequentially. In mature-disc phyllotaxis, when all the elements are the same size, the shape of the spirals is that of Fermat spirals—ideally. That is because Fermat's spiral traverses equal annuli in equal turns. The full model proposed by H. Vogel in 1979^[5] is

{\begin{aligned}r&=c{\sqrt {n}},\\\theta &=n\times 137.508^{\circ },\end{aligned}}

where $θ$ is the angle, $r$ is the radius or distance from the center, and $n$ is the index number of the floret and $c$ is a constant scaling factor. The angle 137.508° is the golden angle which is approximated by ratios of Fibonacci numbers.^[6]

The pattern of florets produced by Vogel's model (central image). The other two images show the patterns for slightly different values of the angle.

The resulting spiral pattern of unit disks should be distinguished from the Doyle spirals, patterns formed by tangent disks of geometrically increasing radii placed on logarithmic spirals.

Solar plants

Fermat's spiral has also been found to be an efficient layout for the mirrors of concentrated solar power plants.^[7]

Related Research Articles

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number $x$ :

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin; its polar angle measured from a fixed polar axis or zenith direction; and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the fixed axis, measured from another fixed reference direction on that plane. When radius is fixed, the two angular coordinates make a coordinate system on the sphere sometimes called spherical polar coordinates.

In mathematics, an $n$ -sphere or hypersphere is an $n$ -dimensional generalization of the 1-dimensional circle and 2-dimensional sphere to any non-negative integer $n$ . The $n$ -sphere is the setting for $n$ -dimensional spherical geometry.

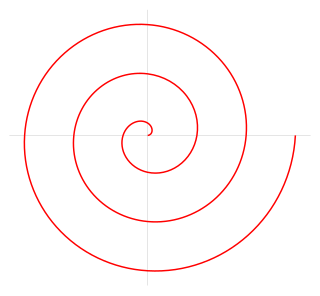
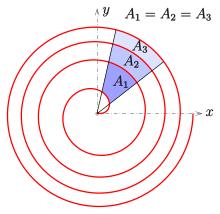
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates $(r, θ)$ it can be described by the equation

<span class="mw-page-title-main">Spiral</span> Curve that winds around a central point

In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.

<span class="mw-page-title-main">Ellipsoid</span> Quadric surface that looks like a deformed sphere

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

<span class="mw-page-title-main">Hyperbolic spiral</span> Spiral asymptotic to a line

A hyperbolic spiral is a plane curve, which can be described in polar coordinates by the equation

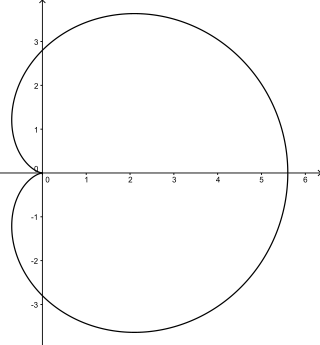
<span class="mw-page-title-main">Cardioid</span> Type of plane curve

In geometry, a cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.

<span class="mw-page-title-main">Nephroid</span> Plane curve; an epicycloid with radii differing by 1/2

In geometry, a nephroid is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger one by a factor of one-half.

This is a table of orthonormalized spherical harmonics that employ the Condon-Shortley phase up to degree $. Some of these formulas are expressed in terms of the Cartesian expansion of the spherical harmonics into polynomials in x, y, z, and r . For purposes of this table, it is useful to express the usual spherical to Cartesian transformations that relate these Cartesian components to and as$

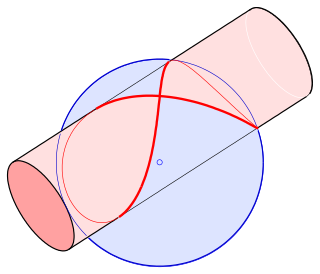
<span class="mw-page-title-main">Viviani's curve</span> Figure-eight shaped curve on a sphere

In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.

In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the $x$ -axis.

The goat grazing problem is either of two related problems in recreational mathematics involving a tethered goat grazing a circular area: the interior grazing problem and the exterior grazing problem. The former involves grazing the interior of a circular area, and the latter, grazing an exterior of a circular area. For the exterior problem, the constraint that the rope can not enter the circular area dictates that the grazing area forms an involute. If the goat were instead tethered to a post on the edge of a circular path of pavement that did not obstruct the goat, the interior and exterior problem would be complements of a simple circular area.

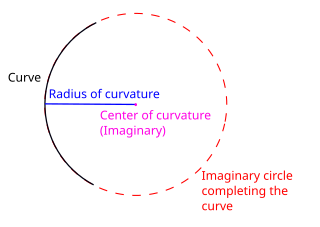
In differential geometry, the radius of curvature, $R$ , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.

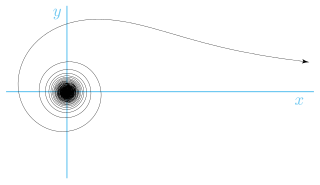
<span class="mw-page-title-main">Lituus (mathematics)</span> Spiral

The lituus spiral is a spiral in which the angle $θ$ is inversely proportional to the square of the radius $r$ .

<span class="mw-page-title-main">Orthoptic (geometry)</span> All points for which two tangents of a curve intersect at 90° angles

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.

<span class="mw-page-title-main">Conical spiral</span> Plane spiral projected onto the surface of a cone

In mathematics, a conical spiral, also known as a conical helix, is a space curve on a right circular cone, whose floor projection is a plane spiral. If the floor projection is a logarithmic spiral, it is called conchospiral.

References

1 2 Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF). Modeling, Identification and Control. 34 (4): 183–198. ISSN 1890-1328. Archived from the original (PDF) on 2020-10-28.
↑ Wicke, Fritz (2013). Einführung in die höhere Mathematik. Springer-Verlag. p. 414. ISBN 978-3-662-36804-6.
↑ Tannery, Paul (ed.). "Lettre de Fermat à Mersenne du 3 juin 1636". Œuvres de Fermat. Vol. 3. p. 277.
↑ Weisstein, Eric W. "Fermat's Spiral". MathWorld . Retrieved 2023-02-04.
↑ Vogel, H. (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.
↑ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.
↑ Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. 86 (2): 792–803. doi:10.1016/j.solener.2011.12.007.

External links

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Lekkas-1] 1 2 Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF). Modeling, Identification and Control. 34 (4): 183–198. ISSN 1890-1328. Archived from the original (PDF) on 2020-10-28.

[2] Wicke, Fritz (2013). Einführung in die höhere Mathematik. Springer-Verlag. p. 414. ISBN 978-3-662-36804-6.

[Fermat-3] Tannery, Paul (ed.). "Lettre de Fermat à Mersenne du 3 juin 1636". Œuvres de Fermat. Vol. 3. p. 277.

[4] Weisstein, Eric W. "Fermat's Spiral". MathWorld . Retrieved 2023-02-04.

[5] Vogel, H. (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.

[6] Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.

[7] Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. 86 (2): 792–803. doi:10.1016/j.solener.2011.12.007.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v t e Pierre de Fermat
Work	Fermat's Last Theorem Fermat number Fermat's principle Fermat's little theorem Fermat polygonal number theorem Fermat pseudoprime Fermat point Fermat's theorem (stationary points) Fermat's theorem on sums of two squares Fermat's spiral Fermat's right triangle theorem
Related	List of things named after Pierre de Fermat Wiles's proof of Fermat's Last Theorem Fermat's Last Theorem in fiction Fermat Prize Fermat's Last Tango (2000 musical) Fermat's Last Theorem (popular science book)