
In number theory, a Carmichael number is a composite number , which in modular arithmetic satisfies the congruence relation:

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair or (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.

The abc conjecture is a conjecture in number theory that arose out of a discussion of Joseph Oesterlé and David Masser in 1985. It is stated in terms of three positive integers and that are relatively prime and satisfy . The conjecture essentially states that the product of the distinct prime factors of is usually not much smaller than . A number of famous conjectures and theorems in number theory would follow immediately from the abc conjecture or its versions. Mathematician Dorian Goldfeld described the abc conjecture as "The most important unsolved problem in Diophantine analysis".
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936, is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that

In number theory, a weird number is a natural number that is abundant but not semiperfect. In other words, the sum of the proper divisors of the number is greater than the number, but no subset of those divisors sums to the number itself.
63 (sixty-three) is the natural number following 62 and preceding 64.
In mathematics, the Lindelöf hypothesis is a conjecture by Finnish mathematician Ernst Leonard Lindelöf about the rate of growth of the Riemann zeta function on the critical line. This hypothesis is implied by the Riemann hypothesis. It says that for any ε > 0,
In number theory, the radical of a positive integer n is defined as the product of the distinct prime numbers dividing n. Each prime factor of n occurs exactly once as a factor of this product:
In number theory, the Elliott–Halberstam conjecture is a conjecture about the distribution of prime numbers in arithmetic progressions. It has many applications in sieve theory. It is named for Peter D. T. A. Elliott and Heini Halberstam, who stated the conjecture in 1968.
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between and for every positive integer . The conjecture is one of Landau's problems (1912) on prime numbers; as of 2024, the conjecture has neither been proved nor disproved.
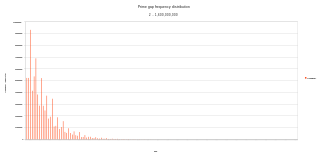
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.

At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about prime numbers. These problems were characterised in his speech as "unattackable at the present state of mathematics" and are now known as Landau's problems. They are as follows:
- Goldbach's conjecture: Can every even integer greater than 2 be written as the sum of two primes?
- Twin prime conjecture: Are there infinitely many primes p such that p + 2 is prime?
- Legendre's conjecture: Does there always exist at least one prime between consecutive perfect squares?
- Are there infinitely many primes p such that p − 1 is a perfect square? In other words: Are there infinitely many primes of the form n2 + 1?

Andrica's conjecture is a conjecture regarding the gaps between prime numbers.

In the theory of probability and statistics, the Dvoretzky–Kiefer–Wolfowitz–Massart inequality provides a bound on the worst case distance of an empirically determined distribution function from its associated population distribution function. It is named after Aryeh Dvoretzky, Jack Kiefer, and Jacob Wolfowitz, who in 1956 proved the inequality

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann, after whom it is named.
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences. In 2014, he received the Cole Prize of the American Mathematical Society.
Oppermann's conjecture is an unsolved problem in mathematics on the distribution of prime numbers. It is closely related to but stronger than Legendre's conjecture, Andrica's conjecture, and Brocard's conjecture. It is named after Danish mathematician Ludvig Oppermann, who announced it in an unpublished lecture in March 1877.























