Related Research Articles
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, a complete coloring is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic numberψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.
In graph theory, toughness is a measure of the connectivity of a graph. A graph G is said to be t-tough for a given real number t if, for every integer k > 1, G cannot be split into k different connected components by the removal of fewer than tk vertices. For instance, a graph is 1-tough if the number of components formed by removing a set of vertices is always at most as large as the number of removed vertices. The toughness of a graph is the maximum t for which it is t-tough; this is a finite number for all finite graphs except the complete graphs, which by convention have infinite toughness.

In graph theory, series–parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
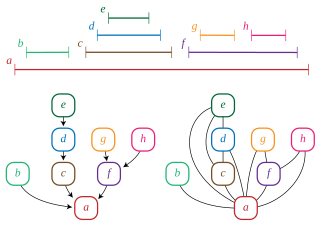
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.
In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.
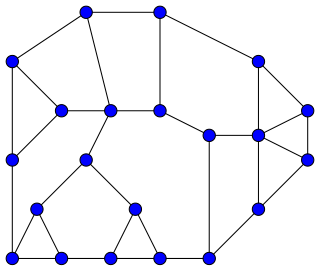
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
In graph theory, a partial k-tree is a type of graph, defined either as a subgraph of a k-tree or as a graph with treewidth at most k. Many NP-hard combinatorial problems on graphs are solvable in polynomial time when restricted to the partial k-trees, for bounded values of k.

In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if is a 2-vertex-connected graph, then the square of is Hamiltonian. It is named after Herbert Fleischner, who published its proof in 1974.
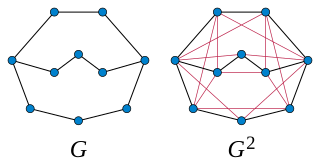
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.
In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.
In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.
In graph theory, a branch of mathematics, a chordal completion of a given undirected graph G is a chordal graph, on the same vertex set, that has G as a subgraph. A minimal chordal completion is a chordal completion such that any graph formed by removing an edge would no longer be a chordal completion. A minimum chordal completion is a chordal completion with as few edges as possible.
In graph theory, an induced matching or strong matching is a subset of the edges of an undirected graph that do not share any vertices and includes every edge connecting any two vertices in the subset.

In graph theory, the cutwidth of an undirected graph is the smallest integer with the following property: there is an ordering of the vertices of the graph, such that every cut obtained by partitioning the vertices into earlier and later subsets of the ordering is crossed by at most edges. That is, if the vertices are numbered , then for every , the number of edges with and is at most .
References
- ↑ Wu, Q. S.; Lu, Chin Lung; Lee, Richard C. T. (2000), "An approximate algorithm for the weighted Hamiltonian path completion problem on a tree", in Lee, D. T.; Teng, Shang-Hua (eds.), Algorithms and Computation, 11th International Conference, ISAAC 2000, Taipei, Taiwan, December 18–20, 2000, Proceedings, Lecture Notes in Computer Science, vol. 1969, Springer, pp. 156–167, doi:10.1007/3-540-40996-3_14
- ↑ Takamizawa, K.; Nishizeki, T.; Saito, N. (1982), "Linear-time computability of combinatorial problems on series–parallel graphs", Journal of the ACM , 29 (3): 623–641, doi: 10.1145/322326.322328 , S2CID 16082154 .
- ↑ Korneyenko, N. M. (1994), "Combinatorial algorithms on a class of graphs", Discrete Applied Mathematics, 54 (2–3): 215–217, doi:10.1016/0166-218X(94)90022-1, MR 1300246
- ↑ Raychaudhuri, Arundhati (1995), "The total interval number of a tree and the Hamiltonian completion number of its line graph", Information Processing Letters, 56 (6): 299–306, doi:10.1016/0020-0190(95)00163-8, MR 1366337
- ↑ Agnetis, A.; Detti, P.; Meloni, C.; Pacciarelli, D. (2001), "A linear algorithm for the Hamiltonian completion number of the line graph of a tree", Information Processing Letters, 79 (1): 17–24, doi:10.1016/S0020-0190(00)00164-2, MR 1832044
- ↑ Detti, Paolo; Meloni, Carlo (2004), "A linear algorithm for the Hamiltonian completion number of the line graph of a cactus", Discrete Applied Mathematics, 136 (2–3): 197–215, doi:10.1016/S0166-218X(03)00441-4, MR 2045212
- ↑ Gamarnik, David; Sviridenko, Maxim (2005), "Hamiltonian completions of sparse random graphs" (PDF), Discrete Applied Mathematics, 152 (1–3): 139–158, doi:10.1016/j.dam.2005.05.001, MR 2174199