Hypercone

Last updated March 23, 2022

Stereographic projection of a spherical cone's generating lines (red), parallels (green) and hypermeridians (blue). Due to conformal property of Stereographic Projection, the curves intersect each other orthogonally (in the yellow points) as in 4D. All curves are circles or straight lines. The generatrices and parallels generates a 3D dual cone. The hypermeridians generates a set of concentric spheres. Spherical cone lines.png — Stereographic projection of a spherical cone's generating lines (red), parallels (green) and hypermeridians (blue). Due to conformal property of Stereographic Projection, the curves intersect each other orthogonally (in the yellow points) as in 4D. All curves are circles or straight lines. The generatrices and parallels generates a 3D dual cone. The hypermeridians generates a set of concentric spheres.

In geometry, a hypercone (or spherical cone) is the figure in the 4-dimensional Euclidean space represented by the equation

It is a quadric surface, and is one of the possible 3-manifolds which are 4-dimensional equivalents of the conical surface in 3 dimensions. It is also named spherical cone because its intersections with hyperplanes perpendicular to the w-axis are spheres. A four-dimensional right spherical hypercone can be thought of as a sphere which expands with time, starting its expansion from a single point source, such that the center of the expanding sphere remains fixed. An oblique spherical hypercone would be a sphere which expands with time, again starting its expansion from a point source, but such that the center of the expanding sphere moves with a uniform velocity.

Parametric form

A right spherical hypercone can be described by the function

{\vec {\sigma }}(\phi ,\theta ,t)=(ts\cos \theta \cos \phi ,ts\cos \theta \sin \phi ,ts\sin \theta ,t)

with vertex at the origin and expansion speed s.

A right spherical hypercone with radius r and height h can be described by the function

{\vec {\sigma }}(\phi ,\theta ,t)=\left(t\cos \phi \sin \theta ,t\sin \phi \sin \theta ,t\cos \theta ,{\frac {h}{r}}t\right)

An oblique spherical hypercone could then be described by the function

{\vec {\sigma }}(\phi ,\theta ,t)=(v_{x}t+ts\cos \theta \cos \phi ,v_{y}t+ts\cos \theta \sin \phi ,v_{z}t+ts\sin \theta ,t)

where $(v_{x},v_{y},v_{z})$ is the 3-velocity of the center of the expanding sphere. An example of such a cone would be an expanding sound wave as seen from the point of view of a moving reference frame: e.g. the sound wave of a jet aircraft as seen from the jet's own reference frame.

Note that the 3D-surfaces above enclose 4D-hypervolumes, which are the 4-cones proper.

Geometrical interpretation

The spherical cone consists of two unbounded nappes, which meet at the origin and are the analogues of the nappes of the 3-dimensional conical surface. The upper nappe corresponds with the half with positive w-coordinates, and the lower nappe corresponds with the half with negative w-coordinates.

If it is restricted between the hyperplanes w = 0 and w = r for some nonzero r, then it may be closed by a 3-ball of radius r, centered at (0,0,0,r), so that it bounds a finite 4-dimensional volume. This volume is given by the formula 1/3 $π$ r⁴, and is the 4-dimensional equivalent of the solid cone. The ball may be thought of as the 'lid' at the base of the 4-dimensional cone's nappe, and the origin becomes its 'apex'.

This shape may be projected into 3-dimensional space in various ways. If projected onto the xyz hyperplane, its image is a ball. If projected onto the xyw, xzw, or yzw hyperplanes, its image is a solid cone. If projected onto an oblique hyperplane, its image is either an ellipsoid or a solid cone with an ellipsoidal base (resembling an ice cream cone). These images are the analogues of the possible images of the solid cone projected to 2 dimensions.

Construction

The (half) hypercone may be constructed in a manner analogous to the construction of a 3D cone. A 3D cone may be thought of as the result of stacking progressively smaller discs on top of each other until they taper to a point. Alternatively, a 3D cone may be regarded as the volume swept out by an upright isosceles triangle as it rotates about its base.

A 4D hypercone may be constructed analogously: by stacking progressively smaller balls on top of each other in the 4th direction until they taper to a point, or taking the hypervolume swept out by a tetrahedron standing upright in the 4th direction as it rotates freely about its base in the 3D hyperplane on which it rests.

Measurements

Hypervolume

The hypervolume of a four-dimensional pyramid and cone is

H={\frac {1}{4}}Vh

where V is the volume of the base and h is the height (the distance between the centre of the base and the apex). For a spherical cone with a base volume of ${\textstyle V={\frac {4}{3}}\pi r^{3}}$ , the hypervolume is

H={\frac {1}{4}}Vh={\frac {1}{4}}\left({\frac {4}{3}}\pi r^{3}\right)h={\frac {1}{3}}\pi r^{3}h

Surface volume

The lateral surface volume of a right spherical cone is ${\textstyle LSV={\frac {4}{3}}\pi r^{2}l}$ where $r$ is the radius of the spherical base and $l$ is the slant height of the cone (the distance between the 2D surface of the sphere and the apex). The surface volume of the spherical base is the same as for any sphere, ${\textstyle {\frac {4}{3}}\pi r^{3}}$ . Therefore, the total surface volume of a right spherical cone can be expressed in the following ways:

Radius and height

${\frac {4}{3}}\pi r^{3}+{\frac {4}{3}}\pi r^{2}{\sqrt {r^{2}+h^{2}}}$
(the volume of the base plus the volume of the lateral 3D surface; the term ${\sqrt {r^{2}+h^{2}}}$ is the slant height)
${\frac {4}{3}}\pi r^{2}\left(r+{\sqrt {r^{2}+h^{2}}}\right)$
where $r$ is the radius and $h$ is the height.

Radius and slant height

${\frac {4}{3}}\pi r^{3}+{\frac {4}{3}}\pi r^{2}l$
${\frac {4}{3}}\pi r^{2}\left(r+l\right)$
where $r$ is the radius and $l$ is the slant height.

Surface area, radius, and slant height

${\frac {1}{3}}Ar+{\frac {1}{3}}Al$
${\frac {1}{3}}A\left(r+l\right)$
where $A$ is the base surface area, $r$ is the radius, and $l$ is the slant height.

Temporal interpretation

If the w-coordinate of the equation of the spherical cone is interpreted as the distance ct, where t is coordinate time and c is the speed of light (a constant), then it is the shape of the light cone in special relativity. In this case, the equation is usually written as:

x^{2}+y^{2}+z^{2}-(ct)^{2}=0,

which is also the equation for spherical wave fronts of light.^[1] The upper nappe is then the future light cone and the lower nappe is the past light cone.^[2]

Related Research Articles

In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during a collision with an atomic nucleus. Cross section is typically denoted $σ$ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.

In mathematics, an $n$ -sphere or a hypersphere is a topological space that is homeomorphic to a standard $n$ -sphere, which is the set of points in $(n + 1)$ -dimensional Euclidean space that are situated at a constant distance $r$ from a fixed point, called the center. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit $n$ -sphere or simply the $n$ -sphere for brevity. In terms of the standard norm, the $n$ -sphere is defined as

In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle from that point.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.

In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

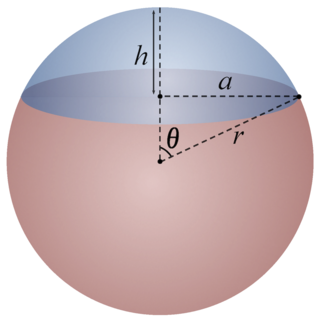
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.

In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.

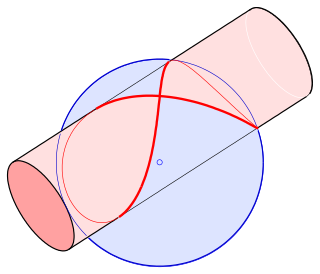
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.

Multiple integral Generalization of definite integrals to functions of multiple variables

In mathematics, a multiple integral is a definite integral of a function of several real variables, for instance, $f (x, y)$ or $f (x, y, z)$ . Integrals of a function of two variables over a region in $are called double integrals, and integrals of a function of three variables over a region in are called triple integrals . For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.$

In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often useful. The defining characteristic of an isotropic chart is that its radial coordinate is defined so that light cones appear round. This means that, the angular isotropic coordinates do not faithfully represent distances within the nested spheres, nor does the radial coordinate faithfully represent radial distances. On the other hand, angles in the constant time hyperslices are represented without distortion, hence the name of the chart.

The method of image charges is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.

Spherical multipole moments are the coefficients in a series expansion of a potential that varies inversely with the distance R to a source, i.e., as 1/R. Examples of such potentials are the electric potential, the magnetic potential and the gravitational potential.

In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.

In geometry, a spherical sector is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap.

In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is adapted to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented.

In four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball of radius r₁ and a line segment of length 2r₂:

In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.

References

↑ A. Halpern (1988). 3000 Solved Problems in Physics. Schaum Series. Mc Graw Hill. p. 689. ISBN 978-0-07-025734-4.
↑ R.G. Lerner, G.L. Trigg (1991). Encyclopedia of Physics (2nd ed.). VHC publishers. p. 1054. ISBN 0-89573-752-3.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] A. Halpern (1988). 3000 Solved Problems in Physics. Schaum Series. Mc Graw Hill. p. 689. ISBN 978-0-07-025734-4.

[2] R.G. Lerner, G.L. Trigg (1991). Encyclopedia of Physics (2nd ed.). VHC publishers. p. 1054. ISBN 0-89573-752-3.

[1]

[2]