The icosian game is a mathematical game invented in 1856 by Irish mathematician William Rowan Hamilton. It involves finding a Hamiltonian cycle on a dodecahedron, a cycle using edges of the dodecahedron that passes through all its vertices. Hamilton sold his work to a game manufacturing company, but it was not commercially successful. Although Hamilton was not the first to study Hamiltonian cycles, his work on this game became the origin of the name of Hamiltonian cycles.
The game's object is to find a cycle among along the edges of a regular dodecahedron, returning to its starting vertex after visiting each vertex a single time. (A cycle visiting all vertices in this way is now called a Hamiltonian cycle.) In a two-player version of the game, one player starts by choosing five consecutive vertices along the cycle, and the other player must complete the cycle. [1]
One version of the game took the form of a flat wooden board inscribed with a planar graph with the same combinatorial structure as the dodecahedron (a Schlegel diagram), [2] with holes for numbered pegs to be placed at its vertices. The cycle found by game players was indicated by the consecutive numbering of the pegs. [3] [4] Another version was shaped as a "partially flattened dodecahedron" with a handle attached to its base. The vertices had fixed pegs. A separate string, with a loop at one end, was wound through these pegs to indicate the cycle. [4]
The game was too easy to play to achieve much popularity. [5] [6]
At the time of his invention of the icosian game, William Rowan Hamilton was the Andrews Professor of Astronomy at Trinity College Dublin and Royal Astronomer of Ireland, and was already famous for his work on Hamiltonian mechanics and his invention of quaternions. [7] The motivation for Hamilton was the problem of understanding the symmetries of the dodecahedron and icosahedron, two dual polyhedra that have the same symmetries as each other. For this purpose he also invented icosian calculus, a system of non-commutative algebra which he used to compute these symmetries. [8]
The name of the icosian game comes from the fact that the icosahedron has twenty faces, the dodecahedron has twenty vertices, and any cycle through all the vertices of the dodecahedron has twenty edges. Icosa is a Greek root meaning twenty. [6] [9] On a dodecahedron with labeled vertices, there are 30 different ways that these vertices could be connected to each other to form a Hamiltonian cycle. However, without the labels, the resulting cycles are all symmetric to each other under rotations and reflections of the dodecahedron. [10]
Both the icosian calculus and the icosian game were outlined by Hamilton in a series of letters to his friend John T. Graves in late 1856. [8] Hamilton then exhibited the game at the 1857 Dublin meeting of the British Association for the Advancement of Science. [11] [12] At the suggestion of Graves, [2] Hamilton sold its publishing rights to Jaques and Son, a London-based toy and game manufacturing company. [8] [11]
This company marketed Hamilton's game beginning in 1859, [3] in both its handheld solid and flat forms, [4] under the lengthy titles The Travellers Dodecahedron, or a voyage around the world, and (respectively) The Icosian Game, invented by Sir William Rowan Hamilton, Royal Astronomer of Ireland; forming a new and highly amusing game for the drawing room, particularly interesting to students in mathematics of illustrating the principles of the Icosian Calculus. [3]
Several other versions of the game were sold in Europe. [10] However, it was not a commercial success. [5] [6] [8] Hamilton received only a £25 licensing fee from Jaques and Son for his invention. [10] Few original copies of the game are known to survive, [13] but one is kept in the library of the Royal Irish Academy in Dublin, [3] and another is included in the collection of the Conservatoire national des arts et métiers in Paris. [2]
Although Hamilton invented the icosian game independently, he was not the first to study Hamiltonian cycles. Knight's tours on chessboards, another puzzle based on Hamiltonian cycles, go back to the 9th century, both in India and in mathematics in the medieval Islamic world. [14] At about the same time as Hamilton, Thomas Kirkman in England was also studying Hamiltonian cycles on polyhedra. [15] Hamilton visited Kirkman in 1861, and presented him with a copy of the icosian game. [8] Despite this related work, some of which was much earlier, Hamiltonian cycles came to be named for Hamilton and for his work on the icosian game. [1]
The icosian game itself has been the topic of multiple works in recreational mathematics by well-known authors on the subject including Édouard Lucas, [16] Wilhelm Ahrens, [17] and Martin Gardner. [10] Puzzles like Hamilton's icosian game, based on finding Hamiltonian cycles in planar graphs, continue to be sold as smartphone apps. [18] Additionally, Maker-Breaker games based on Hamiltonian cycles continue to be an object of study in modern combinatorial game theory. [19] [20] [21] [22] [23] [24]
In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait and disproved by W. T. Tutte, who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.
The Hamiltonian path problem is a topic discussed in the fields of complexity theory and graph theory. It decides if a directed or undirected graph, G, contains a Hamiltonian path, a path that visits every vertex in the graph exactly once. The problem may specify the start and end of the path, in which case the starting vertex s and ending vertex t must be identified.
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details.
The icosian calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856. In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations.
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.
In the mathematical field of graph theory, a quartic graph is a graph where all vertices have degree 4. In other words, a quartic graph is a 4-regular graph.
Thomas Penyngton Kirkman FRS was a British mathematician and ordained minister of the Church of England. Despite being primarily a churchman, he maintained an active interest in research-level mathematics, and was listed by Alexander Macfarlane as one of ten leading 19th-century British mathematicians. In the 1840s, he obtained an existence theorem for Steiner triple systems that founded the field of combinatorial design theory, while the related Kirkman's schoolgirl problem is named after him.
In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.
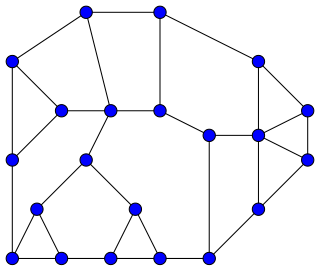
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.
In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.
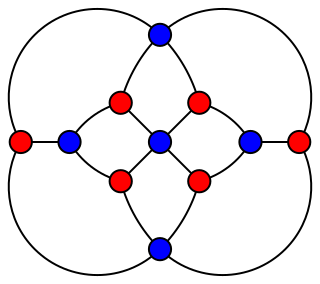
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.
Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.
In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope P is another polyhedron or polytope PK formed by replacing each facet of P with a shallow pyramid. Kleetopes are named after Victor Klee.
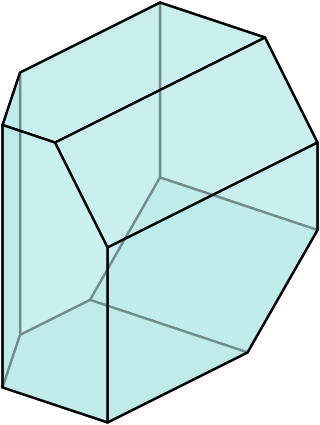
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.
In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.
In the mathematical field of graph theory, the 26-fullerene graph is a polyhedral graph with V = 26 vertices and E = 39 edges. Its planar embedding has three hexagonal faces and twelve pentagonal faces. As a planar graph with only pentagonal and hexagonal faces, meeting in three faces per vertex, this graph is a fullerene. The existence of this fullerene has been known since at least 1968.
In the mathematical field of graph theory, the Barnette–Bosák–Lederberg graph is a cubic polyhedral graph with no Hamiltonian cycle, the smallest such graph possible. It was discovered in the mid-1960s by Joshua Lederberg, David Barnette, and Juraj Bosák, after whom it is named. It has 38 vertices and 57 edges.
