Imre Z. Ruzsa | |
|---|---|
| Born | 23 July 1953 |
| Nationality | |
| Alma mater | Eötvös Loránd University |
| Scientific career | |
| Fields | Mathematics |
Imre Z. Ruzsa (born 23 July 1953) is a Hungarian mathematician specializing in number theory.
Imre Z. Ruzsa | |
|---|---|
| Born | 23 July 1953 |
| Nationality | |
| Alma mater | Eötvös Loránd University |
| Scientific career | |
| Fields | Mathematics |
Imre Z. Ruzsa (born 23 July 1953) is a Hungarian mathematician specializing in number theory.
Ruzsa participated in the International Mathematical Olympiad for Hungary, winning a silver medal in 1969, and two consecutive gold medals with perfect scores in 1970 and 1971. He graduated from the Eötvös Loránd University in 1976. Since then he has been at the Alfréd Rényi Institute of Mathematics of the Hungarian Academy of Sciences. He was awarded the Rollo Davidson Prize in 1988. He was elected corresponding member (1998) and member (2004) of the Hungarian Academy of Sciences. He was invited speaker at the European Congress of Mathematics at Stockholm, 2004, and in the Combinatorics section of the International Congress of Mathematicians in Madrid, 2006. In 2012 he became a fellow of the American Mathematical Society. [1]
With Endre Szemerédi he proved subquadratic upper and lower bounds for the Ruzsa–Szemerédi problem on the number of triples of points in which the union of any three triples contains at least seven points. He proved that an essential component has at least (log x)1+ε elements up to x, for some ε > 0. On the other hand, for every ε > 0 there is an essential component that has at most (log x)1+ε elements up to x, for every x. He gave a new proof to Freiman's theorem. Ruzsa also showed the existence of a Sidon sequence which has at least x0.41 elements up to x.
In a result complementing the Erdős–Fuchs theorem he showed that there exists a sequence a0, a1, ... of natural numbers such that for every n the number of solutions of the inequality ai + aj ≤ n is cn + O(n1/4log n) for some c > 0.
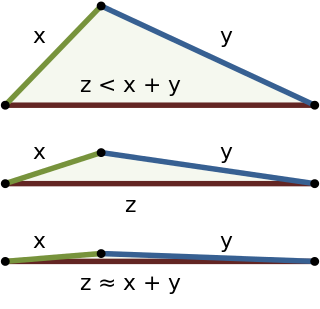
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that
In additive number theory, the Schnirelmann density of a sequence of numbers is a way to measure how "dense" the sequence is. It is named after Russian mathematician Lev Schnirelmann, who was the first to study it.

Endre Szemerédi is a Hungarian-American mathematician and computer scientist, working in the field of combinatorics and theoretical computer science. He has been the State of New Jersey Professor of computer science at Rutgers University since 1986. He also holds a professor emeritus status at the Alfréd Rényi Institute of Mathematics of the Hungarian Academy of Sciences.
In additive combinatorics, Freiman's theorem is a central result which indicates the approximate structure of sets whose sumset is small. It roughly states that if is small, then can be contained in a small generalized arithmetic progression.
In number theory, a Sidon sequence is a sequence of natural numbers in which all pairwise sums are different. Sidon sequences are also called Sidon sets; they are named after the Hungarian mathematician Simon Sidon, who introduced the concept in his investigations of Fourier series.
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences. In 2014, he received the Cole Prize.
Lajos Pósa is a Hungarian mathematician working in the topic of combinatorics, and one of the most prominent mathematics educators of Hungary, best known for his mathematics camps for gifted students. He is a winner of the Széchenyi Prize. Paul Erdős's favorite "child", he discovered theorems at the age of 16. Since 2002, he has worked at the Rényi Institute of the Hungarian Academy of Sciences; earlier he was at the Eötvös Loránd University, at the Departments of Mathematical Analysis, Computer Science.

Gábor J. Székely is a Hungarian-American statistician/mathematician best known for introducing energy statistics (E-statistics). Examples include: the distance correlation, which is a bona fide dependence measure, equals zero exactly when the variables are independent; the distance skewness, which equals zero exactly when the probability distribution is diagonally symmetric; the E-statistic for normality test; and the E-statistic for clustering.
Miklós Simonovits is a Hungarian mathematician who currently works at the Rényi Institute of Mathematics in Budapest and is a member of the Hungarian Academy of Sciences. He is on the advisory board of the journal Combinatorica. He is best known for his work in extremal graph theory and was awarded Széchenyi Prize in 2014. Among other things, he discovered the method of progressive induction which he used to describe graphs which do not contain a predetermined graph and the number of edges is close to maximal. With Lovász, he gave a randomized algorithm using O(n7 log2n) separation calls to approximate the volume of a convex body within a fixed relative error.

In mathematics, the corners theorem is a result in arithmetic combinatorics proved by Miklós Ajtai and Endre Szemerédi. It states that for every , for large enough , any set of at least points in the grid contains a corner, i.e., a triple of points of the form . Later, Solymosi (2003) gave a simpler proof, based on the triangle removal lemma. The corners theorem implies Roth's theorem.
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received the title Centre of Excellence of the European Union (2001). The current director is András Stipsicz. The institute publishes the research journal Studia Scientiarum Mathematicarum Hungarica.
The Erdős–Szemerédi theorem in arithmetic combinatorics states that for every finite set of integers, at least one of , the set of pairwise sums or , the set of pairwise products form a significantly larger set. More precisely, the Erdős–Szemerédi theorem states that there exist positive constants c and such that for any non-empty set

Katalin Marton was a Hungarian mathematician, born in Budapest.
In mathematics, a square-difference-free set is a set of natural numbers, no two of which differ by a square number. Hillel Furstenberg and András Sárközy proved in the late 1970s the Furstenberg–Sárközy theorem of additive number theory showing that, in a certain sense, these sets cannot be very large. In the game of subtract a square, the positions where the next player loses form a square-difference-free set. Another square-difference-free set is obtained by doubling the Moser–de Bruijn sequence.
In graph theory, the graph removal lemma states that when a graph contains few copies of a given subgraph, then all of the copies can be eliminated by removing a small number of edges. The special case in which the subgraph is a triangle is known as the triangle removal lemma.

In combinatorial mathematics and extremal graph theory, the Ruzsa–Szemerédi problem or (6,3)-problem asks for the maximum number of edges in a graph in which every edge belongs to a unique triangle. Equivalently it asks for the maximum number of edges in a balanced bipartite graph whose edges can be partitioned into a linear number of induced matchings, or the maximum number of triples one can choose from points so that every six points contain at most two triples. The problem is named after Imre Z. Ruzsa and Endre Szemerédi, who first proved that its answer is smaller than by a slowly-growing factor.

In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs.

In combinatorics, tripod packing is a problem of finding many disjoint tripods in a three-dimensional grid, where a tripod is an infinite polycube, the union of the grid cubes along three positive axis-aligned rays with a shared apex.
Roth's theorem on arithmetic progressions is a result in additive combinatorics concerning the existence of arithmetic progressions in subsets of the natural numbers. It was first proven by Klaus Roth in 1953. Roth's Theorem is a special case of Szemerédi's Theorem for the case .
In additive combinatorics, the Ruzsa triangle inequality, also known as the Ruzsa difference triangle inequality to differentiate it from some of its variants, bounds the size of the difference of two sets in terms of the sizes of both their differences with a third set. It was proven by Imre Ruzsa (1996), and is so named for its resemblance to the triangle inequality. It is an important lemma in the proof of the Plünnecke-Ruzsa inequality.