Infinity (philosophy)

Last updated

In philosophy and theology, infinity is explored in articles under headings such as the Absolute, God, and Zeno's paradoxes.

Contents

In Greek philosophy, for example in Anaximander, 'the Boundless' is the origin of all that is. He took the beginning or first principle to be an endless, unlimited primordial mass (ἄπειρον, apeiron). The Jain metaphysics and mathematics were the first to define and delineate different "types" of infinities. [1] The work of the mathematician Georg Cantor first placed infinity into a coherent mathematical framework. Keenly aware of his departure from traditional wisdom, Cantor also presented a comprehensive historical and philosophical discussion of infinity. [2] In Christian theology, for example in the work of Duns Scotus, the infinite nature of God invokes a sense of being without constraint, rather than a sense of being unlimited in quantity.

Early thinking

Egyptian

...how sad is the descent in the land of silence, the wakeful sleeps, he who did not slumber at night lies still forever. The scorners say: The dwelling place of the inhabitants of the West is deep and dark, it has no door, no window, no light to illuminate it, no north wind to refresh the heart, the sun does not rise there, but they lie every day in darkness - the guardian has been taken away to the land of infinity...

— an Egyptian mourner [3]

Greek

Anaximander

An early engagement with the idea of infinity was made by Anaximander who considered infinity to be a foundational and primitive basis of reality. [4] Anaximander was the first in the Greek philosophical tradition to propose that the universe was infinite. [5]

Anaxagoras

Anaxagoras (500–428 BCE) was of the opinion that matter of the universe had an innate capacity for infinite division. [6]

The Atomists

A group of thinkers of ancient Greece (later identified as the Atomists) all similarly considered matter to be made of an infinite number of structures as considered by imagining dividing or separating matter from itself an infinite number of times. [7]

Aristotle and after

Aristotle, alive for the period 384–322 BCE, is credited with being the root of a field of thought, in his influence of succeeding thinking for a period spanning more than one subsequent millennium, by his rejection of the idea of actual infinity. [8]

In Book 3 of the work entitled Physics, written by Aristotle, Aristotle deals with the concept of infinity in terms of his notion of actuality and of potentiality. [9] [10] [11]

... It is always possible to think of a larger number: for the number of times a magnitude can be bisected is infinite. Hence the infinite is potential, never actual; the number of parts that can be taken always surpasses any assigned number.

— Physics 207b8

This is often called potential infinity; however, there are two ideas mixed up with this. One is that it is always possible to find a number of things that surpasses any given number, even if there are not actually such things. The other is that we may quantify over infinite sets without restriction. For example, , which reads, "for any integer n, there exists an integer m > n such that P(m)". The second view is found in a clearer form by medieval writers such as William of Ockham:

Sed omne continuum est actualiter existens. Igitur quaelibet pars sua est vere existens in rerum natura. Sed partes continui sunt infinitae quia non tot quin plures, igitur partes infinitae sunt actualiter existentes.

But every continuum is actually existent. Therefore any of its parts is really existent in nature. But the parts of the continuum are infinite because there are not so many that there are not more, and therefore the infinite parts are actually existent.

The parts are actually there, in some sense. However, on this view, no infinite magnitude can have a number, for whatever number we can imagine, there is always a larger one: "There are not so many (in number) that there are no more."

Aristotle's views on the continuum foreshadow some topological aspects of modern mathematical theories of the continuum. Aristotle's emphasis on the connectedness of the continuum may have inspired—in different ways—modern philosophers and mathematicians such as Charles Sanders Peirce, Cantor, and LEJ Brouwer. [12] [13]

Among the scholastics, Aquinas also argued against the idea that infinity could be in any sense complete or a totality.

Aristotle deals with infinity in the context of the prime mover, in Book 7 of the same work, the reasoning of which was later studied and commented on by Simplicius. [14]

Roman

Plotinus

Plotinus considered infinity, while he was alive, during the 3rd century A.D. [4]

Simplicius

Simplicius, [15] alive circa 490 to 560 AD, [16] thought the concept "Mind" was infinite. [15]

Augustine

Augustine thought infinity to be "incomprehensible for the human mind". [15]

Early Indian thinking

The Jain upanga āgama Surya Prajnapti (c. 400 BC) classifies all numbers into three sets: enumerable, innumerable, and infinite. Each of these was further subdivided into three orders:

Jain theory of numbers (See IIIrd section for various infinities) Number theory 1.jpg
Jain theory of numbers (See IIIrd section for various infinities)

The Jains were the first to discard the idea that all infinities were the same or equal. They recognized different types of infinities: infinite in length (one dimension), infinite in area (two dimensions), infinite in volume (three dimensions), and infinite perpetually (infinite number of dimensions).

According to Singh (1987), Joseph (2000) and Agrawal (2000), the highest enumerable number N of the Jains corresponds to the modern concept of aleph-null (the cardinal number of the infinite set of integers 1, 2, ...), the smallest cardinal transfinite number. The Jains also defined a whole system of infinite cardinal numbers, of which the highest enumerable number N is the smallest.

In the Jaina work on the theory of sets, two basic types of infinite numbers are distinguished. On both physical and ontological grounds, a distinction was made between asaṃkhyāta ("countless, innumerable") and ananta ("endless, unlimited"), between rigidly bounded and loosely bounded infinities.

Views from the Renaissance to modern times

Galileo

Galileo Galilei (February 1564 - January 1642 [17] ) discussed the example of comparing the square numbers {1, 4, 9, 16, ...} with the natural numbers {1, 2, 3, 4, ...} as follows:

1 → 1
2 → 4
3 → 9
4 → 16
…

It appeared by this reasoning as though a "set" (Galileo did not use the terminology) which is naturally smaller than the "set" of which it is a part (since it does not contain all the members) is in some sense the same "size". Galileo found no way around this problem:

So far as I see we can only infer that the totality of all numbers is infinite, that the number of squares is infinite, and that the number of their roots is infinite; neither is the number of squares less than the totality of all numbers, nor the latter greater than the former; and finally the attributes "equal," "greater," and "less," are not applicable to infinite, but only to finite, quantities.

— On two New Sciences, 1638

The idea that size can be measured by one-to-one correspondence is today known as Hume's principle, although Hume, like Galileo, believed the principle could not be applied to the infinite. The same concept, applied by Georg Cantor, is used in relation to infinite sets.

Thomas Hobbes

Famously, the ultra-empiricist Hobbes ( April 1588 - December 1679 [18] ) tried to defend the idea of a potential infinity in light of the discovery, by Evangelista Torricelli, of a figure (Gabriel's Horn) whose surface area is infinite, but whose volume is finite. Not reported, this motivation of Hobbes came too late as curves having infinite length yet bounding finite areas were known much before.

John Locke

Locke ( August 1632 - October 1704 [19] ) in common with most of the empiricist philosophers, also believed that we can have no proper idea of the infinite. They believed all our ideas were derived from sense data or "impressions," and since all sensory impressions are inherently finite, so too are our thoughts and ideas. Our idea of infinity is merely negative or privative.

Whatever positive ideas we have in our minds of any space, duration, or number, let them be never so great, they are still finite; but when we suppose an inexhaustible remainder, from which we remove all bounds, and wherein we allow the mind an endless progression of thought, without ever completing the idea, there we have our idea of infinity... yet when we would frame in our minds the idea of an infinite space or duration, that idea is very obscure and confused, because it is made up of two parts very different, if not inconsistent. For let a man frame in his mind an idea of any space or number, as great as he will, it is plain the mind rests and terminates in that idea; which is contrary to the idea of infinity, which consists in a supposed endless progression.

— Essay, II. xvii. 7., author's emphasis

He considered that in considerations on the subject of eternity, which he classified as an infinity, humans are likely to make mistakes. [20]

Modern philosophical views

Modern discussion of the infinite is now regarded as part of set theory and mathematics. Contemporary philosophers of mathematics engage with the topic of infinity and generally acknowledge its role in mathematical practice. But, although set theory is now widely accepted, this was not always so. Influenced by L.E.J Brouwer and verificationism in part, Wittgenstein (April 1889 Vienna - April 1951 Cambridge, England [21] ), made an impassioned attack upon axiomatic set theory, and upon the idea of the actual infinite, during his "middle period". [22]

Does the relation correlate the class of all numbers with one of its subclasses? No. It correlates any arbitrary number with another, and in that way we arrive at infinitely many pairs of classes, of which one is correlated with the other, but which are never related as class and subclass. Neither is this infinite process itself in some sense or other such a pair of classes... In the superstition that correlates a class with its subclass, we merely have yet another case of ambiguous grammar.

— Philosophical Remarks § 141, cf Philosophical Grammar p. 465

Unlike the traditional empiricists, he thought that the infinite was in some way given to sense experience.

... I can see in space the possibility of any finite experience... we recognize [the] essential infinity of space in its smallest part." "[Time] is infinite in the same sense as the three-dimensional space of sight and movement is infinite, even if in fact I can only see as far as the walls of my room.

... what is infinite about endlessness is only the endlessness itself.

Emmanuel Levinas

The philosopher Emmanuel Levinas ( January 1906, Lithuania - December 25 1995, Paris [23] ) uses infinity to designate that which cannot be defined or reduced to knowledge or power. In Levinas' magnum opus Totality and Infinity he says :

...infinity is produced in the relationship of the same with the other, and how the particular and the personal, which are unsurpassable, as it were magnetize the very field in which the production of infinity is enacted...

The idea of infinity is not an incidental notion forged by a subjectivity to reflect the case of an entity encountering on the outside nothing that limits it, overflowing every limit, and thereby infinite. The production of the infinite entity is inseparable from the idea of infinity, for it is precisely in the disproportion between the idea of infinity and the infinity of which it is the idea that this exceeding of limits is produced. The idea of infinity is the mode of being, the infinition, of infinity... All knowing qua intentionality already presupposes the idea of infinity, which is preeminently non-adequation.

— p. 26-27

Levinas also wrote a work entitled Philosophy and the Idea of Infinity, which was published during 1957. [24]

See also

Notes

  1. ↑ Stewart, Ian (2017). Infinity: A Very Short Introduction. Oxford University Press. ISBN   978-0-19-875523-4.
  2. ↑ Newstead, A. (2009). "Cantor on Infinity in Nature, Number, and the Divine Mind" (PDF). American Catholic Philosophical Quarterly. 83 (4): 533–553. doi:10.5840/acpq200983444.
  3. ↑ Henri Frankfort citing Kees, Zeitschrift für aegyptische Sprache in - Ancient Egyptian Religion: An Interpretation, p.108, Courier Corporation, 22 June 2012, ISBN   048614495X Consulted 2017-06-May
  4. 1 2 F. LeRon Shults (2005-11-01). Reforming the Doctrine of God (footnote 4. of page 99). Wm. B. Eerdmans Publishing, 326 pages. ISBN   9780802829887 . Retrieved 2015-06-26.
  5. ↑ A.A. Long (1999-05-28). The Cambridge companion to Early Greek philosophy. Cambridge University Press. p. 127. ISBN   978-0521446679 . Retrieved 2016-03-18.
  6. ↑ James Fieser (2008). The History of Philosophy: A Short Survey. The University of Tennessee at Martin. Retrieved 2016-03-14.
  7. ↑ J.J. O'Connor, E.F. Robertson (February 2002). Infinity. School of Computer Science - University of St Andrews. Retrieved 2016-03-13.
  8. ↑ Rudy Rucker. Infinity: Mathematics. Encyclopædia Britannica. Retrieved 2016-03-13.
  9. ↑ Wolfgang Achtner (2011-02-07). Infinity: New Research Frontiers - Chapter 1 : Infinity as a Transformative concept in Science and Theology (p.22). Cambridge University Press, 7 Feb 2011, edited by Revd Dr Michael Heller, Dr W. Hugh Woodin. ISBN   978-1107003873 . Retrieved 2015-06-21.
  10. ↑ Z. Bechler (1995). Aristotle's Theory of Actuality (p.119). SUNY Press, 1995, 270 pages, SUNY series in ancient Greek philosophy. ISBN   978-0791422403 . Retrieved 2015-06-21.
  11. ↑ John Bowin. Aristotelian Infinity (PDF). University of California - Santa Cruz. Retrieved 2015-06-24.
  12. ↑ Newstead, A.G.J. (2001). Aristotle and modern mathematical theories of the continuum, in Aristotle and Contemporary Science II. Frankfurt: Peter Lang. pp. 113–129.
  13. ↑ White, Michael (1992). The Continuous and the Discrete. Oxford University Press.
  14. ↑ R. Sorabji (C. Hagen) (2014-04-10). Simplicius: On Aristotle Physics 7 (page 1.). A&C Black, 10 Apr 2014, 202 pages, Ancient Commentators on Aristotle. ISBN   978-0801429927 . Retrieved 2015-06-25.
  15. 1 2 3 Dr Adam Drozdek (2013-05-28). Greek Philosophers as Theologians: The Divine Arche. Ashgate Publishing, Ltd. ISBN   978-1409477570.
  16. ↑ J.J. O'Connor and E.F. Robertson (April 1999). Simplicius.{{cite book}}: CS1 maint: numeric names: authors list (link)
  17. ↑ J.J. O'Connor, E.F. Robertson (2002). "Galileo Galilei". St Andrews University. Retrieved 2016-04-21.
  18. ↑ T. Sorell (30 October 2014). "Thomas Hobbes (English philosopher)". Britannica. Retrieved 2016-04-21.
  19. ↑ G.A.J. Rogers (2015-12-14). "John Locke, English philosopher". Britannica. Retrieved 2016-04-21.
  20. ↑ Philosophical beauties selected from the works of John Locke - p.237 T.Hurst 1802 [Retrieved 2015-3-28](ed. Locke writes: And hence it is, that in disputes and reasonings concerning eternity, or any other infinite, we are apt to blunder, and involve ourselves in manifest absurdities...)
  21. ↑ R. Monk (8 April 2016). "Ludwig Wittgenstein, British philosopher". Britannica. Retrieved 2016-04-21.
  22. ↑ See also Asenjo, F. G.; Tamburino, J. (1975). "Logic of antinomies". Notre Dame Journal of Formal Logic. 16: 17–44. doi: 10.1305/ndjfl/1093891610 .
  23. ↑ Bergo, Bettina (23 July 2006). "Emmanual Levinas". Stanford University. Retrieved 2016-04-21.
  24. ↑ E. Levinas - Collected Philosophical Papers (p.47) (Translated by A. Lingis) Springer Science & Business Media, 31 March 1987 ISBN   9024733952 [Retrieved 2015-05-01]

Related Research Articles

The Absolute Infinite is an extension of the idea of infinity proposed by mathematician Georg Cantor.

<span class="mw-page-title-main">Cardinal number</span> Size of a possibly infinite set

In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.

<span class="mw-page-title-main">Cardinality</span> Definition of the number of elements in a set

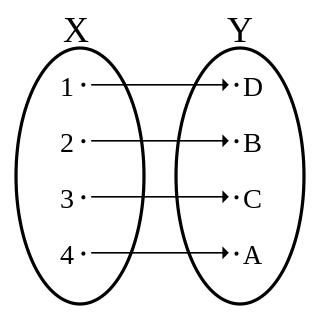
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.

<span class="mw-page-title-main">Georg Cantor</span> German mathematician (1845–1918)

Georg Ferdinand Ludwig Philipp Cantor was a mathematician. He played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

<span class="mw-page-title-main">Set theory</span> Branch of mathematics that studies sets

Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole.

In the philosophy of mathematics, the abstraction of actual infinity involves the acceptance of infinite entities as given, actual and completed objects. These might include the set of natural numbers, extended real numbers, transfinite numbers, or even an infinite sequence of rational numbers. Actual infinity is to be contrasted with potential infinity, in which a non-terminating process produces a sequence with no last element, and where each individual result is finite and is achieved in a finite number of steps. As a result, potential infinity is often formalized using the concept of a limit.

<span class="mw-page-title-main">Infinite set</span> Set that is not a finite set

In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable.

<span class="mw-page-title-main">Zeno of Elea</span> Greek philosopher (c. 495 – c. 430 BC)

Zeno of Elea was a pre-Socratic Greek philosopher. He was a student of Parmenides and one of the Eleatics. Born in Elea, Zeno defended his instructor's belief in monism, the idea that only one single entity exists that makes up all of reality. He rejected the existence of space, time, and motion. To disprove these concepts, he developed a series of paradoxes to demonstrate why these are impossible. Though his original writings are lost, subsequent descriptions by Plato, Aristotle, Diogenes Laertius, and Simplicius of Cilicia have allowed study of his ideas.

Finitism is a philosophy of mathematics that accepts the existence only of finite mathematical objects. It is best understood in comparison to the mainstream philosophy of mathematics where infinite mathematical objects are accepted as legitimate.

Foundations of mathematics is the study of the philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathematics. In this latter sense, the distinction between foundations of mathematics and philosophy of mathematics turns out to be vague. Foundations of mathematics can be conceived as the study of the basic mathematical concepts and how they form hierarchies of more complex structures and concepts, especially the fundamentally important structures that form the language of mathematics also called metamathematical concepts, with an eye to the philosophical aspects and the unity of mathematics. The search for foundations of mathematics is a central question of the philosophy of mathematics; the abstract nature of mathematical objects presents special philosophical challenges.

In mathematics, transfinite numbers or infinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term transfinite was coined in 1895 by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term transfinite also remains in use.

Hume's principle or HP says that the number of Fs is equal to the number of Gs if and only if there is a one-to-one correspondence between the Fs and the Gs. HP can be stated formally in systems of second-order logic. Hume's principle is named for the Scottish philosopher David Hume and was coined by George Boolos.

Galileo's paradox is a demonstration of one of the surprising properties of infinite sets. In his final scientific work, Two New Sciences, Galileo Galilei made apparently contradictory statements about the positive integers. First, a square is an integer which is the square of an integer. Some numbers are squares, while others are not; therefore, all the numbers, including both squares and non-squares, must be more numerous than just the squares. And yet, for every number there is exactly one square; hence, there cannot be more of one than of the other. This is an early use, though not the first, of the idea of one-to-one correspondence in the context of infinite sets.

In mathematical logic, the theory of infinite sets was first developed by Georg Cantor. Although this work has become a thoroughly standard fixture of classical set theory, it has been criticized in several areas by mathematicians and philosophers.

<span class="mw-page-title-main">Fallibilism</span> Philosophical principle

Originally, fallibilism is the philosophical principle that propositions can be accepted even though they cannot be conclusively proven or justified, or that neither knowledge nor belief is certain. The term was coined in the late nineteenth century by the American philosopher Charles Sanders Peirce, as a response to foundationalism. Theorists, following Austrian-British philosopher Karl Popper, may also refer to fallibilism as the notion that knowledge might turn out to be false. Furthermore, fallibilism is said to imply corrigibilism, the principle that propositions are open to revision. Fallibilism is often juxtaposed with infallibilism.

This article contains a discussion of paradoxes of set theory. As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory.

Temporal finitism is the doctrine that time is finite in the past. The philosophy of Aristotle, expressed in such works as his Physics, held that although space was finite, with only void existing beyond the outermost sphere of the heavens, time was infinite. This caused problems for mediaeval Islamic, Jewish, and Christian philosophers who, primarily creationist, were unable to reconcile the Aristotelian conception of the eternal with the Genesis creation narrative.

<span class="mw-page-title-main">Infinity</span> Mathematical concept

Infinity is something which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .

<span class="mw-page-title-main">Eternity of the world</span> Philosophical question

The eternity of the world is the question of whether the world has a beginning in time or has existed from eternity. It was a concern for both ancient philosophers and the medieval theologians and medieval philosophers of the 13th century, and is of interest to modern philosophers and scientists as well. The problem became a focus of a dispute in the 13th century, when some of the works of Aristotle, who believed in the eternity of the world, were rediscovered in the Latin West. This view conflicted with the view of the Catholic Church that the world had a beginning in time. The Aristotelian view was prohibited in the Condemnations of 1210–1277.

In the philosophy of mathematics, Aristotelian realism holds that mathematics studies properties such as symmetry, continuity and order that can be immanently realized in the physical world. It contrasts with Platonism in holding that the objects of mathematics, such as numbers, do not exist in an "abstract" world but can be physically realized. It contrasts with nominalism, fictionalism, and logicism in holding that mathematics is not about mere names or methods of inference or calculation but about certain real aspects of the world.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.