
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.
In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

The Megaminx or Mégaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's Cube.

In graph theory and theoretical computer science, the monochromatic triangle problem is an algorithmic problem on graphs, in which the goal is to partition the edges of a given graph into two triangle-free subgraphs. It is NP-complete but fixed-parameter tractable on graphs of bounded treewidth.

The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the countries of the world, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.
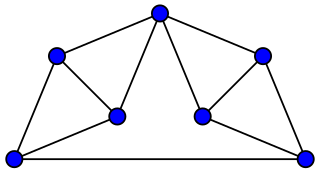
In graph theory, a branch of mathematics, the Moser spindle is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It is a unit distance graph requiring four colors in any graph coloring, and its existence can be used to prove that the chromatic number of the plane is at least four.

The V-Cube 6 is a 6×6×6 version of the original Rubik's Cube. The first mass-produced 6×6×6 was invented by Panagiotis Verdes and is produced by the Greek company Verdes Innovations SA. Other such puzzles have since been introduced by a number of Chinese companies, most of which have mechanisms which improve on the original. Unlike the original puzzle, it has no fixed facets: the center facets are free to move to different positions.

The Impossiball is a rounded icosahedral puzzle similar to the Rubik's Cube. It has a total of 20 movable pieces to rearrange, which is the same as the Rubik's Cube, but all of the Impossiball's pieces are corners, like the Pocket Cube.

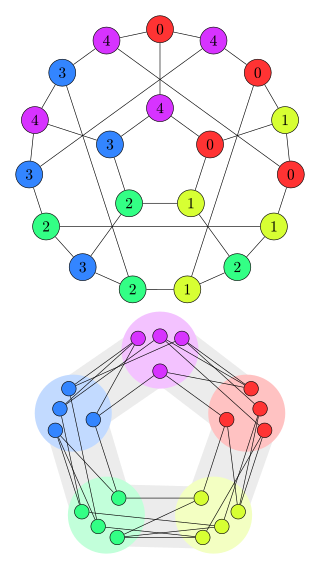
In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.
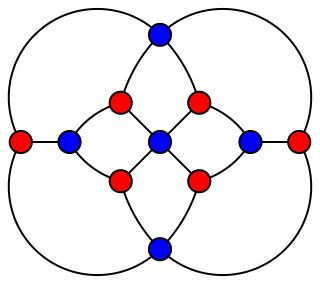
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.

In graph theory, the halved cube graph or half cube graph of dimension n is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.
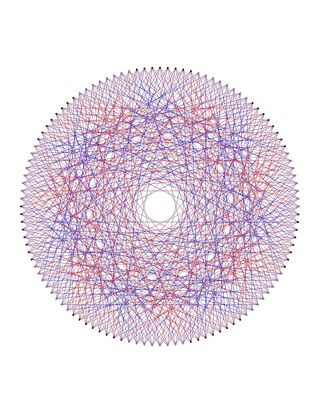
In the mathematical field of graph theory, the Dejter graph is a 6-regular graph with 112 vertices and 336 edges. The Dejter graph is obtained by deleting a copy of the Hamming code of length 7 from the binary 7-cube.

The Gear Cube is a 3-D combination puzzle designed and created by Dutch puzzle maker Oskar van Deventer based on an idea by Bram Cohen. It was initially produced by Shapeways in 2009 and known as "Caution Cube" due to the likelihood of getting one's fingers stuck between the gears while speedcubing. Later, in 2010, it was mass-produced by Meffert's as the "Gear Cube".






















