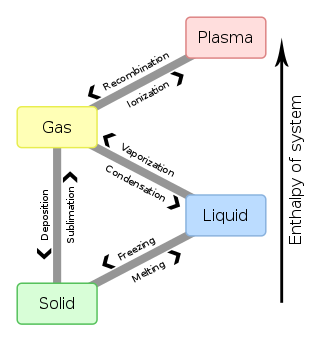
In physics, chemistry, and other related fields like biology, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles Network theory and Percolation.
In theoretical physics, the renormalization group (RG) is a formal apparatus that allows systematic investigation of the changes of a physical system as viewed at different scales. In particle physics, it reflects the changes in the underlying force laws as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle.
The Ising model, named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.
In statistical mechanics, a universality class is a collection of mathematical models which share a single scale-invariant limit under the process of renormalization group flow. While the models within a class may differ dramatically at finite scales, their behavior will become increasingly similar as the limit scale is approached. In particular, asymptotic phenomena such as critical exponents will be the same for all models in the class.
A conformal field theory (CFT) is a quantum field theory that is invariant under conformal transformations. In two dimensions, there is an infinite-dimensional algebra of local conformal transformations, and conformal field theories can sometimes be exactly solved or classified.
In physics, critical phenomena is the collective name associated with the physics of critical points. Most of them stem from the divergence of the correlation length, but also the dynamics slows down. Critical phenomena include scaling relations among different quantities, power-law divergences of some quantities described by critical exponents, universality, fractal behaviour, and ergodicity breaking. Critical phenomena take place in second order phase transitions, although not exclusively.
In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.
The classical XY model is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.
The lambda point is the temperature at which normal fluid helium makes the transition to superfluid state. At pressure of 1 atmosphere, the transition occurs at approximately 2.17 K. The lowest pressure at which He-I and He-II can coexist is the vapor−He-I−He-II triple point at 2.1768 K (−270.9732 °C) and 5.0418 kPa (0.049759 atm), which is the "saturated vapor pressure" at that temperature. The highest pressure at which He-I and He-II can coexist is the bcc−He-I−He-II triple point with a helium solid at 1.762 K (−271.388 °C), 29.725 atm (3,011.9 kPa).
Critical exponents describe the behavior of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e. they do not depend on the details of the physical system, but only on some of its general features. For instance, for ferromagnetic systems at thermal equilibrium, the critical exponents depend only on:
The Kramers–Wannier duality is a symmetry in statistical physics. It relates the free energy of a two-dimensional square-lattice Ising model at a low temperature to that of another Ising model at a high temperature. It was discovered by Hendrik Kramers and Gregory Wannier in 1941. With the aid of this duality Kramers and Wannier found the exact location of the critical point for the Ising model on the square lattice.
In statistical mechanics and quantum field theory, a dangerously irrelevant operator is an operator which is irrelevant at a renormalization group fixed point, yet affects the infrared (IR) physics significantly.
The Binder parameter or Binder cumulant in statistical physics, also known as the fourth-order cumulant is defined as the kurtosis of the order parameter, s, introduced by Austrian theoretical physicist Kurt Binder. It is frequently used to determine accurately phase transition points in numerical simulations of various models.
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.
In theoretical physics, functional renormalization group (FRG) is an implementation of the renormalization group (RG) concept which is used in quantum and statistical field theory, especially when dealing with strongly interacting systems. The method combines functional methods of quantum field theory with the intuitive renormalization group idea of Kenneth G. Wilson. This technique allows to interpolate smoothly between the known microscopic laws and the complicated macroscopic phenomena in physical systems. In this sense, it bridges the transition from simplicity of microphysics to complexity of macrophysics. Figuratively speaking, FRG acts as a microscope with a variable resolution. One starts with a high-resolution picture of the known microphysical laws and subsequently decreases the resolution to obtain a coarse-grained picture of macroscopic collective phenomena. The method is nonperturbative, meaning that it does not rely on an expansion in a small coupling constant. Mathematically, FRG is based on an exact functional differential equation for a scale-dependent effective action.
Jean Zinn-Justin is a French theoretical physicist.
The conformal bootstrap is a non-perturbative mathematical method to constrain and solve conformal field theories, i.e. models of particle physics or statistical physics that exhibit similar properties at different levels of resolution.
In theoretical physics, the curvature renormalization group (CRG) method is an analytical approach to determine the phase boundaries and the critical behavior of topological systems. Topological phases are phases of matter that appear in certain quantum mechanical systems at zero temperature because of a robust degeneracy in the ground-state wave function. They are called topological because they can be described by different (discrete) values of a nonlocal topological invariant. This is to contrast with non-topological phases of matter that can be described by different values of a local order parameter. States with different values of the topological invariant cannot change into each other without a phase transition. The topological invariant is constructed from a curvature function that can be calculated from the bulk Hamiltonian of the system. At the phase transition, the curvature function diverges, and the topological invariant correspondingly jumps abruptly from one value to another. The CRG method works by detecting the divergence in the curvature function, and thus determining the boundaries between different topological phases. Furthermore, from the divergence of the curvature function, it extracts scaling laws that describe the critical behavior, i.e. how different quantities behave as the topological phase transition is approached. The CRG method has been successfully applied to a variety of static, periodically driven, weakly and strongly interacting systems to classify the nature of the corresponding topological phase transitions.
Magnetic 2D materials or magnetic van der Waals materials are two-dimensional materials that display ordered magnetic properties such as antiferromagnetism or ferromagnetism. After the discovery of graphene in 2004, the family of 2D materials has grown rapidly. There have since been reports of several related materials, all except for magnetic materials. But since 2016 there have been numerous reports of 2D magnetic materials that can be exfoliated with ease just like graphene.
