
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.
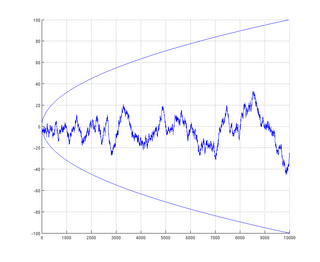
In mathematics, the Mertens conjecture is the statement that the Mertens function is bounded by . Although now disproven, it had been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens, and disproved by Andrew Odlyzko and Herman te Riele . It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.

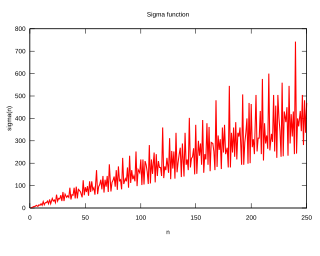
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.

In number theory, the Mertens function is defined for all positive integers n as

Pál Turán also known as Paul Turán, was a Hungarian mathematician who worked primarily in extremal combinatorics.
In mathematics, an untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer. That is, these numbers are not in the image of the aliquot sum function. Their study goes back at least to Abu Mansur al-Baghdadi, who observed that both 2 and 5 are untouchable.
In mathematics, the Lindelöf hypothesis is a conjecture by Finnish mathematician Ernst Leonard Lindelöf about the rate of growth of the Riemann zeta function on the critical line. This hypothesis is implied by the Riemann hypothesis. It says that for any ε > 0, as t tends to infinity. Since ε can be replaced by a smaller value, the conjecture can be restated as follows: for any positive ε,
In mathematics, a superabundant number is a certain kind of natural number. A natural number n is called superabundant precisely when, for all m < n:
In number theory, a colossally abundant number is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
In number theory, friendly numbers are two or more natural numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself. Two numbers with the same "abundancy" form a friendly pair; n numbers with the same abundancy form a friendly n-tuple.

Helmut Maier is a German mathematician and professor at the University of Ulm, Germany. He is known for his contributions in analytic number theory and mathematical analysis and particularly for the so-called Maier's matrix method as well as Maier's theorem for primes in short intervals. He has also done important work in exponential sums and trigonometric sums over special sets of integers and the Riemann zeta function.
In mathematics, the standard conjectures about algebraic cycles are several conjectures describing the relationship of algebraic cycles and Weil cohomology theories. One of the original applications of these conjectures, envisaged by Alexander Grothendieck, was to prove that his construction of pure motives gave an abelian category that is semisimple. Moreover, as he pointed out, the standard conjectures also imply the hardest part of the Weil conjectures, namely the "Riemann hypothesis" conjecture that remained open at the end of the 1960s and was proved later by Pierre Deligne; for details on the link between Weil and standard conjectures, see Kleiman (1968). The standard conjectures remain open problems, so that their application gives only conditional proofs of results. In quite a few cases, including that of the Weil conjectures, other methods have been found to prove such results unconditionally.

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann, after whom it is named.
In mathematics, specifically in number theory, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and

Cameron Leigh Stewart FRSC is a Canadian mathematician. He is a professor of pure mathematics at the University of Waterloo.













