In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing through disjoint pairs among the points are perpendicular, and the four circles passing through any three of the four points have the same radius.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799.

In Euclidean geometry, the medial triangle or midpoint triangle of a triangle △ABC is the triangle with vertices at the midpoints of the triangle's sides AB, AC, BC. It is the n = 3 case of the midpoint polygon of a polygon with n sides. The medial triangle is not the same thing as the median triangle, which is the triangle whose sides have the same lengths as the medians of △ABC.
In Euclidean geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.

In geometry, the de Longchamps point of a triangle is a triangle center named after French mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter.
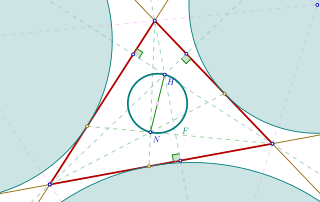
In geometry, the Fuhrmann circle of a triangle, named after the German Wilhelm Fuhrmann (1833–1904), is the circle with a diameter of the line segment between the orthocenter and the Nagel point . This circle is identical with the circumcircle of the Fuhrmann triangle.
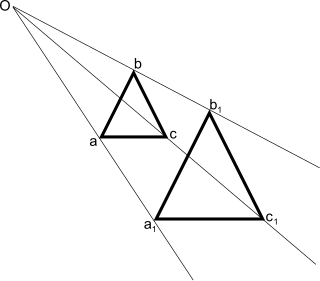
In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation or contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense. If the center is internal, the two figures are scaled mirror images of one another; their angles have the opposite sense.
In geometry, the Exeter point is a special point associated with a plane triangle. The Exeter point is a triangle center and is designated as the center X(22) in Clark Kimberling's Encyclopedia of Triangle Centers. This was discovered in a computers-in-mathematics workshop at Phillips Exeter Academy in 1986. This is one of the recent triangle centers, unlike the classical triangle centers like centroid, incenter, and Steiner point.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In Euclidean geometry, the trillium theorem – is a statement about properties of inscribed and circumscribed circles and their relations.
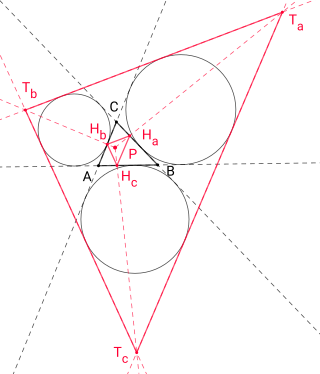
The Clawson point is a special point in a planar triangle defined by the trilinear coordinates , where are the interior angles at the triangle vertices . It is named after John Wentworth Clawson, who published it 1925 in the American Mathematical Monthly.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.
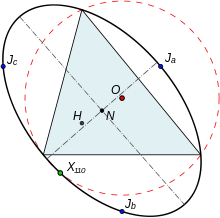
![.mw-parser-output .legend{page-break-inside:avoid;break-inside:avoid-column}.mw-parser-output .legend-color{display:inline-block;min-width:1.25em;height:1.25em;line-height:1.25;margin:1px 0;text-align:center;border:1px solid black;background-color:transparent;color:black}.mw-parser-output .legend-text{}
Johnson circles JA [?] JB [?] JC of radius r (intersect at H; pairs intersect at A, B, C)
Circle passing through A, B, C (has radius r by Johnson's theorem)
Johnson triangle ^JAJBJC of ^ABC
Circumcircle of ^JAJBJC (radius r) Johnson's Theorem.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7e/Johnson%27s_Theorem.svg/300px-Johnson%27s_Theorem.svg.png)
![Johnson circles JA [?] JB [?] JC of radius r (intersect at H; pairs intersect at A, B, C)
Anticomplementary circle of ^ABC (radius 2r); tangent to the Johnson circles at PA, PB, PC
Lines between the common intersection, H, and PA, PB, PC
Anticomplementary triangle ^PAPBPC of ^ABC Johnson's theorem 2.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Johnson%27s_theorem_2.svg/300px-Johnson%27s_theorem_2.svg.png)