
A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, social and economic organizations, an ecosystem, a living cell, and ultimately the entire universe.

Network mapping is the study of the physical connectivity of networks e.g. the Internet. Network mapping discovers the devices on the network and their connectivity. It is not to be confused with network discovery or network enumerating which discovers devices on the network and their characteristics such as. The field of automated network mapping has taken on greater importance as networks become more dynamic and complex in nature.

In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning cluster. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory and percolation.

A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as

A cascading failure is a process in a system of interconnected parts in which the failure of one or few parts can trigger the failure of other parts and so on. Such a failure may happen in many types of systems, including power transmission, computer networking, finance, transportation systems, organisms, the human body, and ecosystems.

In physics, chemistry and materials science, percolation refers to the movement and filtering of fluids through porous materials. It is described by Darcy's law. Broader applications have since been developed that cover connectivity of many systems modeled as lattices or graphs, analogous to connectivity of lattice components in the filtration problem that modulates capacity for percolation.

Network theory is the study of graphs as a representation of either symmetric relations or asymmetric relations between discrete objects. In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes.
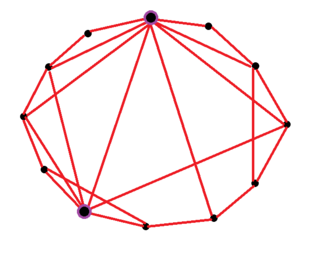
A small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of hops or steps. Specifically, a small-world network is defined to be a network where the typical distance L between two randomly chosen nodes grows proportionally to the logarithm of the number of nodes N in the network, that is:

A transport network, or transportation network is a network or graph in geographic space, describing an infrastructure that permits and constrains movement or flow. Examples include but are not limited to road networks, railways, air routes, pipelines, aqueducts, and power lines. The digital representation of these networks, and the methods for their analysis, is a core part of spatial analysis, geographic information systems, public utilities, and transport engineering. Network analysis is an application of the theories and algorithms of Graph theory and is a form of proximity analysis.

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e., the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
In applied probability theory, the Simon model is a class of stochastic models that results in a power-law distribution function. It was proposed by Herbert A. Simon to account for the wide range of empirical distributions following a power-law. It models the dynamics of a system of elements with associated counters. In this model the dynamics of the system is based on constant growth via addition of new elements as well as incrementing the counters at a rate proportional to their current values.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

The study of interdependent networks is a subfield of network science dealing with phenomena caused by the interactions between complex networks. Though there may be a wide variety of interactions between networks, dependency focuses on the scenario in which the nodes in one network require support from nodes in another network. For an example of infrastructure dependency see Fig. 1.
The field of complex networks has emerged as an important area of science to generate novel insights into nature of complex systems The application of network theory to climate science is a young and emerging field. To identify and analyze patterns in global climate, scientists model climate data as complex networks.

In network theory, multidimensional networks, a special type of multilayer network, are networks with multiple kinds of relations. Increasingly sophisticated attempts to model real-world systems as multidimensional networks have yielded valuable insight in the fields of social network analysis, economics, urban and international transport, ecology, psychology, medicine, biology, commerce, climatology, physics, computational neuroscience, operations management, infrastructures and finance.

Targeted immunization strategies are approaches designed to increase the immunization level of populations and decrease the chances of epidemic outbreaks. Though often in regards to use in healthcare practices and the administration of vaccines to prevent biological epidemic outbreaks, these strategies refer in general to immunization schemes in complex networks, biological, social or artificial in nature. Identification of at-risk groups and individuals with higher odds of spreading the disease often plays an important role in these strategies.
Robustness, the ability to withstand failures and perturbations, is a critical attribute of many complex systems including complex networks.

In network science, a hub is a node with a number of links that greatly exceeds the average. Emergence of hubs is a consequence of a scale-free property of networks. While hubs cannot be observed in a random network, they are expected to emerge in scale-free networks. The uprise of hubs in scale-free networks is associated with power-law distribution. Hubs have a significant impact on the network topology. Hubs can be found in many real networks, such as the brain or the Internet.











