Lepage test

Last updated

In statistics, the Lepage test is an exact distribution-free test (nonparametric test) for jointly monitoring the location (central tendency) and scale (variability) in two-sample treatment versus control comparisons. It is a rank test for the two-sample location-scale problem. The Lepage test statistic is the squared Euclidean distance of the standardized Wilcoxon rank-sum test for location and the standardized Ansari–Bradley test for scale. The Lepage test was first introduced by Yves Lepage in 1971 in a paper in Biometrika. [1] A large number of Lepage-type tests exists in statistical literature for simultaneously testing location and scale shifts in case-control studies. The details may be found in the book: Nonparametric statistical tests: A computational approach. [2] Wolfgang Kössler [3] in 2006 also introduced various Lepage type tests using some alternative score functions optimal for various distributions. Amitava Mukherjee and Marco Marozzi introduced a class of percentile modified versions of the Lepage test. [4] An alternative to the Lepage-type tests is known as the Cucconi test proposed by Odoardo Cucconi in 1968. [5]

Contents

Conducting the Lepage test with R

Practitioners can apply the Lepage test using the pLepage function of the contributory package NSM3, [6] built under R software. Andreas Schulz and Markus Neuhäuser also provided detailed R code for computation of test statistic and p-value of the Lepage test [7] for the users.

Application in statistical process monitoring

In recent years, the Lepage statistic is a widely used statistical process for monitoring and quality control. In 2012, Amitava Mukherjee and Subhabrata Chakraborti introduced a distribution-free Shewhart-type Phase-II monitoring scheme [8] (control chart) for simultaneously monitoring of location and scale parameter of a process using a test sample of fixed size, when a reference sample of sufficiently large size is available from an in-control population. Later in 2015, the same statisticians along with Shovan Chowdhury, proposed a distribution-free CUSUM-type Phase-II monitoring scheme [9] based on the Lepage statistic. In 2017, Mukherjee further designed an EWMA-type distribution-free Phase-II monitoring scheme [10] for joint monitoring of location and scale. In the same year, Mukherjee, with Marco Marozzi, known for promoting the Cucconi test, came together to design the Circular-Grid Lepage chart – a new type of joint monitoring scheme. [11]

Multisample version of the Lepage test

In 2005, František Rublìk introduced the multisample version of the original two-sample Lepage test. [12]

See also

Related Research Articles

<span class="mw-page-title-main">Kolmogorov–Smirnov test</span> Non-parametric statistical test between two distributions

In statistics, the Kolmogorov–Smirnov test is a nonparametric test of the equality of continuous, one-dimensional probability distributions that can be used to test whether a sample came from a given reference probability distribution, or to test whether two samples came from the same distribution. Intuitively, the test provides a method to qualitatively answer the question "How likely is it that we would see a collection of samples like this if they were drawn from that probability distribution?" or, in the second case, "How likely is it that we would see two sets of samples like this if they were drawn from the same probability distribution?". It is named after Andrey Kolmogorov and Nikolai Smirnov.

Nonparametric statistics is a type of statistical analysis that makes minimal assumptions about the underlying distribution of the data being studied. Often these models are infinite-dimensional, rather than finite dimensional, as is parametric statistics. Nonparametric statistics can be used for descriptive statistics or statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are evidently violated.

Mann–Whitney test is a nonparametric test of the null hypothesis that, for randomly selected values X and Y from two populations, the probability of X being greater than Y is equal to the probability of Y being greater than X.

Student's t-test is a statistical test used to test whether the difference between the response of two groups is statistically significant or not. It is any statistical hypothesis test in which the test statistic follows a Student's t-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known. When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's t distribution. The t-test's most common application is to test whether the means of two populations are significantly different. In many cases, a Z-test will yield very similar results to a t-test since the latter converges to the former as the size of the dataset increases.

<span class="mw-page-title-main">Mathematical statistics</span> Branch of statistics

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.

<span class="mw-page-title-main">Kruskal–Wallis test</span> Non-parametric method for testing whether samples originate from the same distribution

The Kruskal–Wallis test by ranks, Kruskal–Wallis test, or one-way ANOVA on ranks is a non-parametric method for testing whether samples originate from the same distribution. It is used for comparing two or more independent samples of equal or different sample sizes. It extends the Mann–Whitney U test, which is used for comparing only two groups. The parametric equivalent of the Kruskal–Wallis test is the one-way analysis of variance (ANOVA).

The Wilcoxon signed-rank test is a non-parametric rank test for statistical hypothesis testing used either to test the location of a population based on a sample of data, or to compare the locations of two populations using two matched samples. The one-sample version serves a purpose similar to that of the one-sample Student's t-test. For two matched samples, it is a paired difference test like the paired Student's t-test. The Wilcoxon test can be a good alternative to the t-test when population means are not of interest; for example, when one wishes to test whether a population's median is nonzero, or whether there is a better than 50% chance that a sample from one population is greater than a sample from another population.

<span class="texhtml mvar" style="font-style:italic;">x̅</span> and R chart

In statistical process control (SPC), the and R chart is a type of scheme, popularly known as control chart, used to monitor the mean and range of a normally distributed variables simultaneously, when samples are collected at regular intervals from a business or industrial process. It is often used to monitor the variables data but the performance of the and R chart may suffer when the normality assumption is not valid.

In statistics, the Behrens–Fisher problem, named after Walter-Ulrich Behrens and Ronald Fisher, is the problem of interval estimation and hypothesis testing concerning the difference between the means of two normally distributed populations when the variances of the two populations are not assumed to be equal, based on two independent samples.

The sign test is a statistical method to test for consistent differences between pairs of observations, such as the weight of subjects before and after treatment. Given pairs of observations for each subject, the sign test determines if one member of the pair tends to be greater than the other member of the pair.

<span class="mw-page-title-main">Q–Q plot</span> Plot of the empirical distribution of p-values against the theoretical one

In statistics, a Q–Q plot (quantile–quantile plot) is a probability plot, a graphical method for comparing two probability distributions by plotting their quantiles against each other. A point (x, y) on the plot corresponds to one of the quantiles of the second distribution (y-coordinate) plotted against the same quantile of the first distribution (x-coordinate). This defines a parametric curve where the parameter is the index of the quantile interval.

Kendall's W is a non-parametric statistic for rank correlation. It is a normalization of the statistic of the Friedman test, and can be used for assessing agreement among raters and in particular inter-rater reliability. Kendall's W ranges from 0 to 1.

<span class="mw-page-title-main">Dirichlet process</span> Family of stochastic processes

In probability theory, Dirichlet processes are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose range is itself a set of probability distributions. It is often used in Bayesian inference to describe the prior knowledge about the distribution of random variables—how likely it is that the random variables are distributed according to one or another particular distribution.

In statistics, the Hodges–Lehmann estimator is a robust and nonparametric estimator of a population's location parameter. For populations that are symmetric about one median, such as the Gaussian or normal distribution or the Student t-distribution, the Hodges–Lehmann estimator is a consistent and median-unbiased estimate of the population median. For non-symmetric populations, the Hodges–Lehmann estimator estimates the "pseudo–median", which is closely related to the population median.

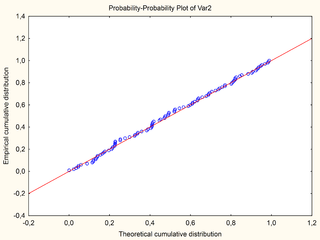
<span class="mw-page-title-main">P–P plot</span> Probability plot which compares two cumulative distribution functions

In statistics, a P–P plot is a probability plot for assessing how closely two data sets agree, or for assessing how closely a dataset fits a particular model. It works by plotting the two cumulative distribution functions against each other; if they are similar, the data will appear to be nearly a straight line. This behavior is similar to that of the more widely used Q–Q plot, with which it is often confused.

The logrank test, or log-rank test, is a hypothesis test to compare the survival distributions of two samples. It is a nonparametric test and appropriate to use when the data are right skewed and censored. It is widely used in clinical trials to establish the efficacy of a new treatment in comparison with a control treatment when the measurement is the time to event. The test is sometimes called the Mantel–Cox test. The logrank test can also be viewed as a time-stratified Cochran–Mantel–Haenszel test.

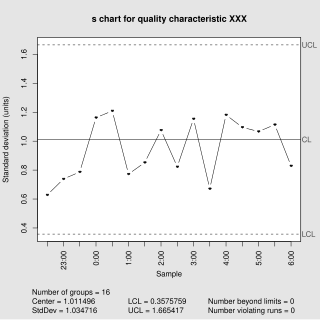
<span class="texhtml mvar" style="font-style:italic;">x̅</span> and s chart

In statistical quality control, the and s chart is a type of control chart used to monitor variables data when samples are collected at regular intervals from a business or industrial process. This is connected to traditional statistical quality control (SQC) and statistical process control (SPC). However, Woodall noted that "I believe that the use of control charts and other monitoring methods should be referred to as “statistical process monitoring,” not “statistical process control (SPC).”"

In statistics, the Cucconi test is a nonparametric test for jointly comparing central tendency and variability in two samples. Many rank tests have been proposed for the two-sample location-scale problem. Nearly all of them are Lepage-type tests, that is a combination of a location test and a scale test. The Cucconi test was first proposed by Odoardo Cucconi in 1968.

Jean Dickinson Gibbons is an American statistician, an expert in nonparametric statistics and an author of books on statistics. She was the first chair of the Committee on Women in Statistics of the American Statistical Association, and the Jean Dickinson Gibbons Graduate Program in Statistics at Virginia Tech is named for her.

Distribution-free (nonparametric) control charts are one of the most important tools of statistical process monitoring and control. Implementation techniques of distribution-free control charts do not require any knowledge about the underlying process distribution or its parameters. The main advantage of distribution-free control charts is its in-control robustness, in the sense that, irrespective of the nature of the underlying process distributions, the properties of these control charts remain the same when the process is smoothly operating without presence of any assignable cause.

References

  1. ↑ Lepage, Yves (April 1971). "A Combination of Wilcoxon's and Ansari-Bradley's Statistics". Biometrika. 58 (1): 213–217. doi:10.2307/2334333. ISSN   0006-3444. JSTOR   2334333.
  2. ↑ Neuhäuser, Markus (2011-12-19). Nonparametric Statistical Tests. Chapman and Hall/CRC. doi:10.1201/b11427. ISBN   9781439867037.
  3. ↑ Kössler, W. (Wolfgang) (2006). Asymptotic power and efficiency of lepage-type tests for the treatment of combined location-scale alternatives. Humboldt-Universität zu Berlin. doi:10.18452/2462. hdl:18452/3114. OCLC   243600853.
  4. ↑ Mukherjee, Amitava; Marozzi, Marco (2019-08-01). "A class of percentile modified Lepage-type tests". Metrika. 82 (6): 657–689. doi:10.1007/s00184-018-0700-1. ISSN   1435-926X.
  5. ↑ Cucconi, Odoardo (1968). "Un Nuovo Test non Parametrico per Il Confronto Fra Due Gruppi di Valori Campionari". Giornale Degli Economisti e Annali di Economia. 27 (3/4): 225–248. JSTOR   23241361.
  6. ↑ Schneider, Grant; Chicken, Eric; Becvarik, Rachel (2018-05-16), NSM3: Functions and Datasets to Accompany Hollander, Wolfe, and Chicken – Nonparametric Statistical Methods, Third Edition , retrieved 2019-09-17
  7. ↑ Schulz, Andreas. "R Programme for Lepage Test" (PDF).
  8. ↑ Mukherjee, A.; Chakraborti, S. (2011-09-26). "A Distribution-free Control Chart for the Joint Monitoring of Location and Scale". Quality and Reliability Engineering International. 28 (3): 335–352. doi:10.1002/qre.1249. ISSN   0748-8017.
  9. ↑ Chowdhury, Shovan; Mukherjee, Amitava; Chakraborti, Subhabrata (2014-11-07). "Distribution-free Phase II CUSUM Control Chart for Joint Monitoring of Location and Scale" (PDF). Quality and Reliability Engineering International. 31 (1): 135–151. doi:10.1002/qre.1677. hdl: 2263/50153 . ISSN   0748-8017.
  10. ↑ Mukherjee, Amitava (2017-02-18). "Distribution-free phase-II exponentially weighted moving average schemes for joint monitoring of location and scale based on subgroup samples". The International Journal of Advanced Manufacturing Technology. 92 (1–4): 101–116. doi:10.1007/s00170-016-9977-2. ISSN   0268-3768.
  11. ↑ Mukherjee, Amitava; Marozzi, Marco (2016-05-17). "Distribution-free Lepage Type Circular-grid Charts for Joint Monitoring of Location and Scale Parameters of a Process". Quality and Reliability Engineering International. 33 (2): 241–274. doi:10.1002/qre.2002. ISSN   0748-8017.
  12. ↑ Rublík, František (2005). "The multisample version of the Lepage test". Kybernetika. 41 (6): [713]–733. hdl:10338.dmlcz/135688. ISSN   0023-5954.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.