
The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.

Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries over physical space.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. It can be used to calculate the informational difference between measurements.

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In differential topology, the jet bundle is a certain construction that makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form. Jets may also be seen as the coordinate free versions of Taylor expansions.
The Nambu–Goto action is the simplest invariant action in bosonic string theory, and is also used in other theories that investigate string-like objects. It is the starting point of the analysis of zero-thickness string behavior, using the principles of Lagrangian mechanics. Just as the action for a free point particle is proportional to its proper time — i.e., the "length" of its world-line — a relativistic string's action is proportional to the area of the sheet which the string traces as it travels through spacetime.
In physics, the Polyakov action is an action of the two-dimensional conformal field theory describing the worldsheet of a string in string theory. It was introduced by Stanley Deser and Bruno Zumino and independently by L. Brink, P. Di Vecchia and P. S. Howe in 1976, and has become associated with Alexander Polyakov after he made use of it in quantizing the string in 1981. The action reads
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, on a complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study.
In physics, a sigma model is a field theory that describes the field as a point particle confined to move on a fixed manifold. This manifold can be taken to be any Riemannian manifold, although it is most commonly taken to be either a Lie group or a symmetric space. The model may or may not be quantized. An example of the non-quantized version is the Skyrme model; it cannot be quantized due to non-linearities of power greater than 4. In general, sigma models admit (classical) topological soliton solutions, for example, the Skyrmion for the Skyrme model. When the sigma field is coupled to a gauge field, the resulting model is described by Ginzburg–Landau theory. This article is primarily devoted to the classical field theory of the sigma model; the corresponding quantized theory is presented in the article titled "non-linear sigma model".
In theoretical physics, the Wess–Zumino model has become the first known example of an interacting four-dimensional quantum field theory with linearly realised supersymmetry. In 1974, Julius Wess and Bruno Zumino studied, using modern terminology, dynamics of a single chiral superfield whose cubic superpotential leads to a renormalizable theory.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.
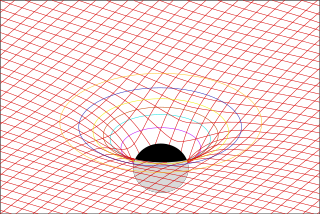
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
In statistics, the multivariate t-distribution is a multivariate probability distribution. It is a generalization to random vectors of the Student's t-distribution, which is a distribution applicable to univariate random variables. While the case of a random matrix could be treated within this structure, the matrix t-distribution is distinct and makes particular use of the matrix structure.
In computational chemistry, a constraint algorithm is a method for satisfying the Newtonian motion of a rigid body which consists of mass points. A restraint algorithm is used to ensure that the distance between mass points is maintained. The general steps involved are: (i) choose novel unconstrained coordinates, (ii) introduce explicit constraint forces, (iii) minimize constraint forces implicitly by the technique of Lagrange multipliers or projection methods.

In theoretical physics, relativistic Lagrangian mechanics is Lagrangian mechanics applied in the context of special relativity and general relativity.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.




























































