
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
In mathematics, the matrix representation of conic sections permits the tools of linear algebra to be used in the study of conic sections. It provides easy ways to calculate a conic section's axis, vertices, tangents and the pole and polar relationship between points and lines of the plane determined by the conic. The technique does not require putting the equation of a conic section into a standard form, thus making it easier to investigate those conic sections whose axes are not parallel to the coordinate system.
In mathematics, a degenerate case is a limiting case of a class of objects which appears to be qualitatively different from the rest of the class; "degeneracy" is the condition of being a degenerate case.
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings.
Probability is a measure of the likeliness that an event will occur. Probability is used to quantify an attitude of mind towards some proposition whose truth is not certain. The proposition of interest is usually of the form "A specific event will occur." The attitude of mind is of the form "How certain is it that the event will occur?" The certainty that is adopted can be described in terms of a numerical measure, and this number, between 0 and 1 is called the probability. Probability theory is used extensively in statistics, mathematics, science and philosophy to draw conclusions about the likelihood of potential events and the underlying mechanics of complex systems.

In geometry, a degenerate conic is a conic that fails to be an irreducible curve. This means that the defining equation is factorable over the complex numbers as the product of two linear polynomials.

In geometry, a locus is a set of all points, whose location satisfies or is determined by one or more specified conditions.

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution.

In geometry, focuses or foci are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.
In mathematics and statistics, an asymptotic distribution is a probability distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators.
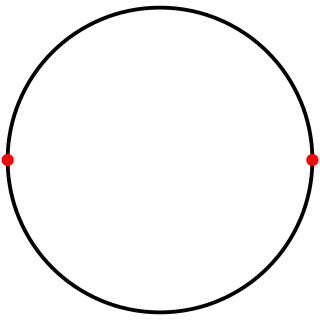
In geometry, a digon, or a 2-gon, is a polygon with two sides (edges) and two vertices. Its construction is degenerate in a Euclidean plane because either the two sides would coincide or one or both would have to be curved; however, it can be easily visualised in elliptic space. It may also be viewed as a representation of a graph with two vertices, see "Generalized polygon".
In probability theory, a member of the (a, b, 0) class of distributions is any distribution of a discrete random variable N whose values are nonnegative integers whose probability mass function satisfies the recurrence formula

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event. It can also be used for the number of events in other types of intervals than time, and in dimension greater than 1.
In statistics, a zero-inflated model is a statistical model based on a zero-inflated probability distribution, i.e. a distribution that allows for frequent zero-valued observations.










