In mathematics, logic, and computer science, a type theory is the formal presentation of a specific type system, and type theory in general is the academic study of type systems.
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning.

In lambda calculus, the Church–Rosser theorem states that, when applying reduction rules to terms, the ordering in which the reductions are chosen does not make a difference to the eventual result.
Curry's paradox is a paradox in which an arbitrary claim F is proved from the mere existence of a sentence C that says of itself "If C, then F", requiring only a few apparently innocuous logical deduction rules. Since F is arbitrary, any logic having these rules allows one to prove everything. The paradox may be expressed in natural language and in various logics, including certain forms of set theory, lambda calculus, and combinatory logic.
In mathematical logic, sequent calculus is a style of formal logical argumentation in which every line of a proof is a conditional tautology instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the natural style of deduction used by mathematicians than to David Hilbert's earlier style of formal logic, in which every line was an unconditional tautology. More subtle distinctions may exist; for example, propositions may implicitly depend upon non-logical axioms. In that case, sequents signify conditional theorems in a first-order language rather than conditional tautologies.
In programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and mathematical proofs.
Intuitionistic type theory is a type theory and an alternative foundation of mathematics. Intuitionistic type theory was created by Per Martin-Löf, a Swedish mathematician and philosopher, who first published it in 1972. There are multiple versions of the type theory: Martin-Löf proposed both intensional and extensional variants of the theory and early impredicative versions, shown to be inconsistent by Girard's paradox, gave way to predicative versions. However, all versions keep the core design of constructive logic using dependent types.
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered. From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus, but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason, the CoC and its variants have been the basis for Coq and other proof assistants.
System F is a typed lambda calculus that introduces, to simply typed lambda calculus, a mechanism of universal quantification over types. System F formalizes parametric polymorphism in programming languages, thus forming a theoretical basis for languages such as Haskell and ML. It was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds.
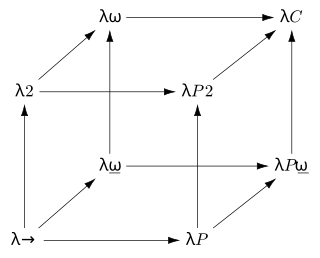
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen in his landmark 1934 paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively. The cut-elimination theorem states that any judgement that possesses a proof in the sequent calculus making use of the cut rule also possesses a cut-free proof, that is, a proof that does not make use of the cut rule.
Bunched logic is a variety of substructural logic proposed by Peter O'Hearn and David Pym. Bunched logic provides primitives for reasoning about resource composition, which aid in the compositional analysis of computer and other systems. It has category-theoretic and truth-functional semantics, which can be understood in terms of an abstract concept of resource, and a proof theory in which the contexts Γ in an entailment judgement Γ ⊢ A are tree-like structures (bunches) rather than lists or (multi)sets as in most proof calculi. Bunched logic has an associated type theory, and its first application was in providing a way to control the aliasing and other forms of interference in imperative programs. The logic has seen further applications in program verification, where it is the basis of the assertion language of separation logic, and in systems modelling, where it provides a way to decompose the resources used by components of a system.
In mathematical logic, structural proof theory is the subdiscipline of proof theory that studies proof calculi that support a notion of analytic proof, a kind of proof whose semantic properties are exposed. When all the theorems of a logic formalised in a structural proof theory have analytic proofs, then the proof theory can be used to demonstrate such things as consistency, provide decision procedures, and allow mathematical or computational witnesses to be extracted as counterparts to theorems, the kind of task that is more often given to model theory.
In computer science and logic, a dependent type is a type whose definition depends on a value. It is an overlapping feature of type theory and type systems. In intuitionistic type theory, dependent types are used to encode logic's quantifiers like "for all" and "there exists". In functional programming languages like Agda, ATS, Coq, F*, Epigram, and Idris, dependent types help reduce bugs by enabling the programmer to assign types that further restrain the set of possible implementations.
The simply typed lambda calculus, a form of type theory, is a typed interpretation of the lambda calculus with only one type constructor that builds function types. It is the canonical and simplest example of a typed lambda calculus. The simply typed lambda calculus was originally introduced by Alonzo Church in 1940 as an attempt to avoid paradoxical use of the untyped lambda calculus.
Twelf is an implementation of the logical framework LF developed by Frank Pfenning and Carsten Schürmann at Carnegie Mellon University. It is used for logic programming and for the formalization of programming language theory.
In mathematical logic and computer science the symbol ⊢ has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails".
In the branches of mathematical logic known as proof theory and type theory, a pure type system (PTS), previously known as a generalized type system (GTS), is a form of typed lambda calculus that allows an arbitrary number of sorts and dependencies between any of these. The framework can be seen as a generalisation of Barendregt's lambda cube, in the sense that all corners of the cube can be represented as instances of a PTS with just two sorts. In fact, Barendregt (1991) framed his cube in this setting. Pure type systems may obscure the distinction between types and terms and collapse the type hierarchy, as is the case with the calculus of constructions, but this is not generally the case, e.g. the simply typed lambda calculus allows only terms to depend on terms.
A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.







