Lorentz oscillator model

Last updated October 10, 2024

Electrons are bound to the atomic nucleus analogously to springs of different strengths, AKA springs that are not isotropic, AKA anisotropic. Atom-spring.svg — Electrons are bound to the atomic nucleus analogously to springs of different strengths, AKA springs that are not isotropic, AKA anisotropic.

The Lorentz oscillator model describes the optical response of bound charges. The model is named after the Dutch physicist Hendrik Antoon Lorentz. It is a classical, phenomenological model for materials with characteristic resonance frequencies (or other characteristic energy scales) for optical absorption, e.g. ionic and molecular vibrations, interband transitions (semiconductors), phonons, and collective excitations.^[1]^[2]

Derivation of electron motion

The model is derived by modeling an electron orbiting a massive, stationary nucleus as a spring-mass-damper system.^[2]^[3]^[4] The electron is modeled to be connected to the nucleus via a hypothetical spring and its motion is damped by via a hypothetical damper. The damping force ensures that the oscillator's response is finite at its resonance frequency. For a time-harmonic driving force which originates from the electric field, Newton's second law can be applied to the electron to obtain the motion of the electron and expressions for the dipole moment, polarization, susceptibility, and dielectric function.^[4]

Equation of motion for electron oscillator: ${\begin{aligned}\mathbf {F} _{\text{net}}=\mathbf {F} _{\text{damping}}+\mathbf {F} _{\text{spring}}+\mathbf {F} _{\text{driving}}&=m{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}\\[1ex]{\frac {-m}{\tau }}{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}-k\mathbf {r} -{e}\mathbf {E} (t)&=m{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}\\[1ex]{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}+{\frac {1}{\tau }}{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}+\omega _{0}^{2}\mathbf {r} \;&=\;{\frac {-e}{m}}\mathbf {E} (t)\end{aligned}}$

where

$\mathbf {r}$ is the displacement of charge from the rest position,
$t$ is time,
$\tau$ is the relaxation time/scattering time,
$k$ is a constant factor characteristic of the spring,
$m$ is the effective mass of the electron,
${\textstyle \omega _{0}={\sqrt {k/m}}}$ is the resonance frequency of the oscillator,
$e$ is the elementary charge,
$\mathbf {E} (t)$ is the electric field.

For time-harmonic fields: $\mathbf {E} (t)=\mathbf {E} _{0}e^{-i\omega t}$ $\mathbf {r} (t)=\mathbf {r} _{0}e^{-i\omega t}$

The stationary solution of this equation of motion is: $\mathbf {r} (\omega )={\frac {\frac {-e}{m}}{\omega _{0}^{2}-\omega ^{2}-i\omega /\tau }}\mathbf {E} (\omega )$

The fact that the above solution is complex means there is a time delay (phase shift) between the driving electric field and the response of the electron's motion.^[4]

Dipole moment

The displacement, $\mathbf {r}$ , induces a dipole moment, $\mathbf {p}$ , given by $\mathbf {p} (\omega )=-e\mathbf {r} (\omega )={\hat {\alpha }}(\omega )\mathbf {E} (\omega ).$

${\hat {\alpha }}(\omega )$ is the polarizability of single oscillator, given by ${\hat {\alpha }}(\omega )={\frac {e^{2}}{m}}{\frac {1}{(\omega _{0}^{2}-\omega ^{2})-i\omega /\tau }}.$

Three distinct scattering regimes can be interpreted corresponding to the dominant denominator term in the dipole moment:^[5]

Regime	Condition	Dispersion Scaling	Phase Shift
Thomson scattering	$\omega ^{2}\gg {\frac {\omega }{\tau }},\omega _{0}^{2}$	$1$	0°
Shneider-Miles scattering	${\frac {\omega }{\tau }}\gg \|\omega _{0}^{2}-\omega ^{2}\|$	$\omega ^{2}$	90°
Rayleigh scattering	$\omega _{0}^{2}\gg \omega ^{2},{\frac {\omega }{\tau }}$	$\omega ^{4}$	180°

Polarization

The polarization $\mathbf {P}$ is the dipole moment per unit volume. For macroscopic material properties N is the density of charges (electrons) per unit volume. Considering that each electron is acting with the same dipole moment we have the polarization as below $\mathbf {P} =N\mathbf {p} =N{\hat {\alpha }}(\omega )\mathbf {E} (\omega ).$

Electric displacement

The electric displacement $\mathbf {D}$ is related to the polarization density $\mathbf {P}$ by $\mathbf {D} ={\hat {\varepsilon }}\mathbf {E} =\mathbf {E} +4\pi \mathbf {P} =(1+4\pi N{\hat {\alpha }})\mathbf {E}$

Dielectric function

The complex dielectric function is given by ${\hat {\varepsilon }}(\omega )=1+{\frac {4\pi Ne^{2}}{m}}{\frac {1}{(\omega _{0}^{2}-\omega ^{2})-i\omega /\tau }}$ where $4\pi Ne^{2}/m=\omega _{p}^{2}$ and $\omega _{p}$ is the so-called plasma frequency.

In practice, the model is commonly modified to account for multiple absorption mechanisms present in a medium. The modified version is given by^[7] ${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon _{\infty }+\sum _{j}\chi _{j}^{L}(\omega$ where ${\displaystyle \chi _{j}^{L}(\omega$ and

$\varepsilon _{\infty }$ is the value of the dielectric function at infinite frequency, which can be used as an adjustable parameter to account for high frequency absorption mechanisms,
$s_{j}=\omega _{p}^{2}f_{j}$ and $f_{j}$ is related to the strength of the $j$ th absorption mechanism,
$\Gamma _{j}=1/\tau$ .

Separating the real and imaginary components, ${\hat {\varepsilon }}(\omega )=\varepsilon _{1}(\omega )+i\varepsilon _{2}(\omega )=\left[\varepsilon _{\infty }+\sum _{j}{\frac {s_{j}(\omega _{0,j}^{2}-\omega ^{2})}{\left(\omega _{0,j}^{2}-\omega ^{2}\right)^{2}+\left(\Gamma _{j}\omega \right)^{2}}}\right]+i\left[\sum _{j}{\frac {s_{j}(\Gamma _{j}\omega )}{\left(\omega _{0,j}^{2}-\omega ^{2}\right)^{2}+\left(\Gamma _{j}\omega \right)^{2}}}\right]$

Complex conductivity

The complex optical conductivity in general is related to the complex dielectric function ${\hat {\sigma }}(\omega )={\frac {\omega }{4\pi i}}\left({\hat {\varepsilon }}(\omega )-1\right)$

Substituting the formula of ${\hat {\varepsilon }}(\omega )$ in the equation above we obtain ${\hat {\sigma }}(\omega )={\frac {Ne^{2}}{m}}{\frac {\omega }{\omega /\tau +i\left(\omega _{0}^{2}-\omega ^{2}\right)}}$

Separating the real and imaginary components, ${\hat {\sigma }}(\omega )=\sigma _{1}(\omega )+i\sigma _{2}(\omega )={\frac {Ne^{2}}{m}}{\frac {\frac {\omega ^{2}}{\tau }}{\left(\omega _{0}^{2}-\omega ^{2}\right)^{2}+\omega ^{2}/\tau ^{2}}}-i{\frac {Ne^{2}}{m}}{\frac {\left(\omega _{0}^{2}-\omega ^{2}\right)\omega }{\left(\omega _{0}^{2}-\omega ^{2}\right)^{2}+\omega ^{2}/\tau ^{2}}}$

Related Research Articles

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x: $where k is a positive constant.$

Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.

Power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. Power is a scalar quantity.

<span class="mw-page-title-main">Torque</span> Turning force around an axis

In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force. The symbol for torque is typically $, the lowercase Greek letter tau . When being referred to as moment of force, it is commonly denoted by M . Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque, which is applied by the screwdriver rotating around its axis. A force of three newtons applied two metres from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum.$

In statistical mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force with that of the total potential energy of the system. Mathematically, the theorem states $where T is the total kinetic energy of the N particles, F k represents the force on the k th particle, which is located at position r k, and angle brackets represent the average over time of the enclosed quantity. The word virial for the right-hand side of the equation derives from vis, the Latin word for "force" or "energy", and was given its technical definition by Rudolf Clausius in 1870.$

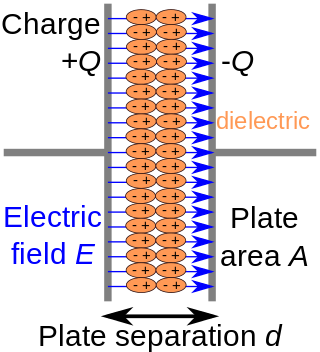
In electromagnetism, a dielectric is an electrical insulator that can be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the material as they do in an electrical conductor, because they have no loosely bound, or free, electrons that may drift through the material, but instead they shift, only slightly, from their average equilibrium positions, causing dielectric polarisation. Because of dielectric polarisation, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. This creates an internal electric field that reduces the overall field within the dielectric itself. If a dielectric is composed of weakly bonded molecules, those molecules not only become polarised, but also reorient so that their symmetry axes align to the field.

<span class="mw-page-title-main">Permittivity</span> Measure of the electric polarizability of a dielectric material

In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter $ε$ (epsilon), is a measure of the electric polarizability of a dielectric material. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.

In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity $ε$ , composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as $where the vector r is the relative position between the charges. This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/ r 2, the average number of particles at each distance r is proportional to r 2, assuming the fluid is fairly isotropic. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.$

<span class="mw-page-title-main">Path integral formulation</span> Formulation of quantum mechanics

The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

A Maxwell material is the most simple model viscoelastic material showing properties of a typical liquid. It shows viscous flow on the long timescale, but additional elastic resistance to fast deformations. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid. A generalization of the scalar relation to a tensor equation lacks motivation from more microscopic models and does not comply with the concept of material objectivity. However, these criteria are fulfilled by the Upper-convected Maxwell model.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.

In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.

In quantum physics, Fermi's golden rule is a formula that describes the transition rate from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time and is proportional to the strength of the coupling between the initial and final states of the system as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth.

The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:

In classical electromagnetism, reciprocity refers to a variety of related theorems involving the interchange of time-harmonic electric current densities (sources) and the resulting electromagnetic fields in Maxwell's equations for time-invariant linear media under certain constraints. Reciprocity is closely related to the concept of symmetric operators from linear algebra, applied to electromagnetism.

<span class="mw-page-title-main">Larmor formula</span> Gives the total power radiated by an accelerating, nonrelativistic point charge

In electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J. Larmor in 1897, in the context of the wave theory of light.

In the physics of electromagnetism, the Abraham–Lorentz force is the reaction force on an accelerating charged particle caused by the particle emitting electromagnetic radiation by self-interaction. It is also called the radiation reaction force, the radiation damping force, or the self-force. It is named after the physicists Max Abraham and Hendrik Lorentz.

In electrical engineering, dielectric loss quantifies a dielectric material's inherent dissipation of electromagnetic energy. It can be parameterized in terms of either the loss angle $δ$ or the corresponding loss tangent $tan(δ)$ . Both refer to the phasor in the complex plane whose real and imaginary parts are the resistive (lossy) component of an electromagnetic field and its reactive (lossless) counterpart.

Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the electrostatic force or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle.

Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.

References

↑ Lorentz, Hendrik Antoon (1909). The theory of electrons and its applications to the phenomena of light and radiant heat. Vol. Bd. XXIX, Bd. 29. New York; Leipzig: B.G. Teubner. OCLC 535812.
1 2 Dressel, Martin; Grüner, George (2002). "Semiconductors". Electrodynamics of Solids: Optical Properties of Electrons in Matter. Cambridge. pp. 136–172. doi:10.1017/CBO9780511606168.008. ISBN 9780521592536.{{cite book}}: CS1 maint: location missing publisher (link)
↑ Almog, I. F.; Bradley, M. S.; Bulovic, V. (2011). "The Lorentz Oscillator and its Applications" (PDF). Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science. Massachusetts Institute of Technology. Retrieved 2021-11-24.
1 2 3 Colton, John (2020). "Lorentz Oscillator Model" (PDF). Brigham Young University, Department of Physics & Astronomy. Brigham Young University. Retrieved 2021-11-18.
↑ Patel, Adam (2021). "Thomson and collisional regimes of in-phase coherent microwave scattering off gaseous microplasmas". Scientific Reports. 11 (1). doi: 10.1038/s41598-021-02500-y . PMC 8642454 .
↑ Spitzer, W. G.; Kleinman, D.; Walsh, D. (1959). "Infrared Properties of Hexagonal Silicon Carbide". Physical Review. 113 (1): 127–132. Bibcode:1959PhRv..113..127S. doi:10.1103/PhysRev.113.127 . Retrieved 2021-11-24.
↑ Zhang, Z. M.; Lefever-Button, G.; Powell, F. R. (1998). "Infrared Refractive Index and Extinction Coefficient of Polyimide Films". International Journal of Thermophysics. 19 (3): 905–916. doi:10.1023/A:1022655309574. S2CID 116271335 . Retrieved 2021-11-24.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Lorentz1909-1] Lorentz, Hendrik Antoon (1909). The theory of electrons and its applications to the phenomena of light and radiant heat. Vol. Bd. XXIX, Bd. 29. New York; Leipzig: B.G. Teubner. OCLC 535812.

[Dressel2002-2] 1 2 Dressel, Martin; Grüner, George (2002). "Semiconductors". Electrodynamics of Solids: Optical Properties of Electrons in Matter. Cambridge. pp. 136–172. doi:10.1017/CBO9780511606168.008. ISBN 9780521592536.{{cite book}}: CS1 maint: location missing publisher (link)

[Almog2011-3] Almog, I. F.; Bradley, M. S.; Bulovic, V. (2011). "The Lorentz Oscillator and its Applications" (PDF). Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science. Massachusetts Institute of Technology. Retrieved 2021-11-24.

[Colton2020-4] 1 2 3 Colton, John (2020). "Lorentz Oscillator Model" (PDF). Brigham Young University, Department of Physics & Astronomy. Brigham Young University. Retrieved 2021-11-18.

[Patel2021-5] Patel, Adam (2021). "Thomson and collisional regimes of in-phase coherent microwave scattering off gaseous microplasmas". Scientific Reports. 11 (1). doi: 10.1038/s41598-021-02500-y . PMC 8642454 .

[Spitzer1959-6] Spitzer, W. G.; Kleinman, D.; Walsh, D. (1959). "Infrared Properties of Hexagonal Silicon Carbide". Physical Review. 113 (1): 127–132. Bibcode:1959PhRv..113..127S. doi:10.1103/PhysRev.113.127 . Retrieved 2021-11-24.

[Zhang1998-7] Zhang, Z. M.; Lefever-Button, G.; Powell, F. R. (1998). "Infrared Refractive Index and Extinction Coefficient of Polyimide Films". International Journal of Thermophysics. 19 (3): 905–916. doi:10.1023/A:1022655309574. S2CID 116271335 . Retrieved 2021-11-24.

[1]

[2]

[3]

[4]

[5]

[7]