The Lydersen method [1] is a group contribution method for the estimation of critical properties temperature (Tc), pressure (Pc) and volume (Vc). The Lydersen method is the prototype for and ancestor of many new models like Joback, [2] Klincewicz, [3] Ambrose, [4] Gani-Constantinou [5] and others.
The Lydersen method is based in case of the critical temperature on the Guldberg rule which establishes a relation between the normal boiling point and the critical temperature.
Guldberg has found that a rough estimate of the normal boiling point Tb, when expressed in kelvins (i.e., as an absolute temperature), is approximately two-thirds of the critical temperature Tc. Lydersen uses this basic idea but calculates more accurate values.
M is the molar mass and Gi are the group contributions (different for all three properties) for functional groups of a molecule.
| Group | Gi (Tc) | Gi (Pc) | Gi (Vc) | Group | Gi (Tc) | Gi (Pc) | Gi (Vc) |
|---|---|---|---|---|---|---|---|
| -CH3,-CH2- | 0.020 | 0.227 | 55.0 | >CH | 0.012 | 0.210 | 51.0 |
| -C< | - | 0,210 | 41.0 | =CH2,#CH | 0.018 | 0,198 | 45.0 |
| =C<,=C= | - | 0.198 | 36.0 | =C-H,#C- | 0.005 | 0.153 | 36.0 |
| -CH2-(Ring) | 0.013 | 0.184 | 44.5 | >CH-(Ring) | 0.012 | 0.192 | 46.0 |
| >C<(Ring) | -0.007 | 0.154 | 31.0 | =CH-,=C<,=C=(Ring) | 0.011 | 0.154 | 37.0 |
| -F | 0.018 | 0.224 | 18.0 | -Cl | 0.017 | 0.320 | 49.0 |
| -Br | 0.010 | 0.500 | 70.0 | -I | 0.012 | 0.830 | 95.0 |
| -OH | 0.082 | 0.060 | 18.0 | -OH(Aromat) | 0.031 | -0.020 | 3.0 |
| -O- | 0.021 | 0.160 | 20.0 | -O-(Ring) | 0.014 | 0.120 | 8.0 |
| >C=O | 0.040 | 0.290 | 60.0 | >C=O(Ring) | 0.033 | 0.200 | 50.0 |
| HC=O- | 0.048 | 0.330 | 73.0 | -COOH | 0.085 | 0.400 | 80.0 |
| -COO- | 0.047 | 0.470 | 80.0 | -NH2 | 0.031 | 0.095 | 28.0 |
| >NH | 0.031 | 0.135 | 37.0 | >NH(Ring) | 0.024 | 0.090 | 27.0 |
| >N | 0.014 | 0.170 | 42.0 | >N-(Ring) | 0.007 | 0.130 | 32.0 |
| -CN | 0.060 | 0.360 | 80.0 | -NO2 | 0.055 | 0.420 | 78.0 |
| -SH,-S- | 0.015 | 0.270 | 55.0 | -S-(Ring) | 0.008 | 0.240 | 45.0 |
| =S | 0.003 | 0.240 | 47.0 | >Si< | 0.030 | 0.540 | - |
| -B< | 0.030 | - | - |
Acetone is fragmented in two different groups, one carbonyl group and two methyl groups. For the critical volume the following calculation results:
Vc = 40 + 60.0 + 2 * 55.0 = 210 cm3
In the literature (such as in the Dortmund Data Bank) the values 215.90 cm3, [6] 230.5 cm3 [7] and 209.0 cm3 [8] are published.
The density, of a substance is its mass per unit volume. The symbol most often used for density is ρ, although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars.
The enthalpy of vaporization, also known as the (latent) heat of vaporization or heat of evaporation, is the amount of energy (enthalpy) that must be added to a liquid substance to transform a quantity of that substance into a gas. The enthalpy of vaporization is a function of the pressure at which that transformation takes place.
Vapor pressure or equilibrium vapor pressure is defined as the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases at a given temperature in a closed system. The equilibrium vapor pressure is an indication of a liquid's evaporation rate. It relates to the tendency of particles to escape from the liquid. A substance with a high vapor pressure at normal temperatures is often referred to as volatile. The pressure exhibited by vapor present above a liquid surface is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases. As the kinetic energy of the molecules increases, the number of molecules transitioning into a vapor also increases, thereby increasing the vapor pressure.
The Lennard-Jones potential is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions.
In thermodynamics, a critical point is the end point of a phase equilibrium curve. The most prominent example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas cannot be liquefied by pressure alone. At the critical point, defined by a critical temperatureTc and a critical pressurepc, phase boundaries vanish. Other examples include the liquid–liquid critical points in mixtures, and the ferromagnet-paramagnet transition in the absence of an external magnetic field.
In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample. In some fields such as signal processing and econometrics it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form. One of the famous applications of kernel density estimation is in estimating the class-conditional marginal densities of data when using a naive Bayes classifier, which can improve its prediction accuracy.
In statistics, a generalized additive model (GAM) is a generalized linear model in which the linear response variable depends linearly on unknown smooth functions of some predictor variables, and interest focuses on inference about these smooth functions.
The non-random two-liquid model is an activity coefficient model that correlates the activity coefficients of a compound with its mole fractions in the liquid phase concerned. It is frequently applied in the field of chemical engineering to calculate phase equilibria. The concept of NRTL is based on the hypothesis of Wilson that the local concentration around a molecule is different from the bulk concentration. This difference is due to a difference between the interaction energy of the central molecule with the molecules of its own kind and that with the molecules of the other kind . The energy difference also introduces a non-randomness at the local molecular level. The NRTL model belongs to the so-called local-composition models. Other models of this type are the Wilson model, the UNIQUAC model, and the group contribution model UNIFAC. These local-composition models are not thermodynamically consistent for a one-fluid model for a real mixture due to the assumption that the local composition around molecule i is independent of the local composition around molecule j. This assumption is not true, as was shown by Flemr in 1976. However, they are consistent if a hypothetical two-liquid model is used.
Parachor is a quantity related to surface tension that was proposed by S. Sugden in 1924. It is defined according to the formula:
The Joback method predicts eleven important and commonly used pure component thermodynamic properties from molecular structure only.
UNIQUAC is an activity coefficient model used in description of phase equilibria. The model is a so-called lattice model and has been derived from a first order approximation of interacting molecule surfaces in statistical thermodynamics. The model is however not fully thermodynamically consistent due to its two liquid mixture approach. In this approach the local concentration around one central molecule is assumed to be independent from the local composition around another type of molecule.
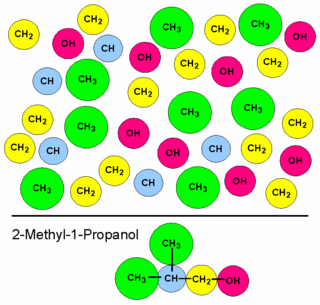
In thermodynamic theory, the Klincewicz method is a predictive method based both on group contributions and on a correlation with some basic molecular properties. The method estimates the critical temperature, the critical pressure, and the critical volume of pure components.
A group-contribution method in chemistry is a technique to estimate and predict thermodynamic and other properties from molecular structures.
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
PSRK is an estimation method for the calculation of phase equilibria of mixtures of chemical components. The original goal for the development of this method was to enable the estimation of properties of mixtures containing supercritical components. This class of substances cannot be predicted with established models, for example UNIFAC.
Aksel Lydersen was a Norwegian engineer and professor in chemical engineering at the Norwegian Institute of Technology. He was also active in the Norwegian language conflict and was leader of the Riksmål Society in Norway 1969 to 1974.
Moving horizon estimation (MHE) is an optimization approach that uses a series of measurements observed over time, containing noise and other inaccuracies, and produces estimates of unknown variables or parameters. Unlike deterministic approaches, MHE requires an iterative approach that relies on linear programming or nonlinear programming solvers to find a solution.
VTPR is an estimation method for the calculation of phase equilibria of mixtures of chemical components. The original goal for the development of this method was to enable the estimation of properties of mixtures which contain supercritical components. These class of substances couldn't be predicted with established models like UNIFAC.
The shear viscosity of a fluid is a material property that describes the friction between internal neighboring fluid surfaces flowing with different fluid velocities. This friction is the effect of (linear) momentum exchange caused by molecules with sufficient energy to move between these fluid sheets due to fluctuations in their motion. The viscosity is not a material constant, but a material property that depends on temperature, pressure, fluid mixture composition, local velocity variations. This functional relationship is described by a mathematical viscosity model called a constitutive equation which is usually far more complex than the defining equation of shear viscosity. One such complicating feature is the relation between the viscosity model for a pure fluid and the model for a fluid mixture which is called mixing rules. When scientists and engineers use new arguments or theories to develop a new viscosity model, instead of improving the reigning model, it may lead to the first model in a new class of models. This article will display one or two representative models for different classes of viscosity models, and these classes are:
