Related Research Articles

A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as

In physics, chemistry, and materials science, percolation refers to the movement and filtering of fluids through porous materials. It is described by Darcy's law. Broader applications have since been developed that cover connectivity of many systems modeled as lattices or graphs, analogous to connectivity of lattice components in the filtration problem that modulates capacity for percolation.

In mathematics, computer science and network science, network theory is a part of graph theory. It defines networks as graphs where the nodes or edges possess attributes. Network theory analyses these networks over the symmetric relations or asymmetric relations between their (discrete) components.
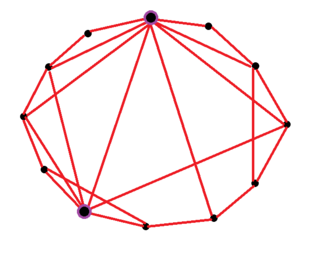
A small-world network is a graph characterized by a high clustering coefficient and low distances. On an example of social network, high clustering implies the high probability that two friends of one person are friends themselves. The low distances, on the other hand, mean that there is a short chain of social connections between any two people. Specifically, a small-world network is defined to be a network where the typical distance L between two randomly chosen nodes grows proportionally to the logarithm of the number of nodes N in the network, that is:

Albert-László Barabási is a Romanian-born Hungarian-American physicist, best known for his discoveries in network science and network medicine.

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.

In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.
In the study of complex networks, assortative mixing, or assortativity, is a bias in favor of connections between network nodes with similar characteristics. In the specific case of social networks, assortative mixing is also known as homophily. The rarer disassortative mixing is a bias in favor of connections between dissimilar nodes.

A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who are already wealthy receive more than those who are not. "Preferential attachment" is only the most recent of many names that have been given to such processes. They are also referred to under the names Yule process, cumulative advantage, the rich get richer, and the Matthew effect. They are also related to Gibrat's law. The principal reason for scientific interest in preferential attachment is that it can, under suitable circumstances, generate power law distributions. If preferential attachment is non-linear, measured distributions may deviate from a power law. These mechanisms may generate distributions which are approximately power law over transient periods.

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
In applied probability theory, the Simon model is a class of stochastic models that results in a power-law distribution function. It was proposed by Herbert A. Simon to account for the wide range of empirical distributions following a power-law. It models the dynamics of a system of elements with associated counters. In this model the dynamics of the system is based on constant growth via addition of new elements as well as incrementing the counters at a rate proportional to their current values.
Mixing patterns refer to systematic tendencies of one type of nodes in a network to connect to another type. For instance, nodes might tend to link to others that are very similar or very different. This feature is common in many social networks, although it also appears sometimes in non-social networks. Mixing patterns are closely related to assortativity; however, for the purposes of this article, the term is used to refer to assortative or disassortative mixing based on real-world factors, either topological or sociological.

The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability p, or more generally a critical surface for a group of parameters p1, p2, ..., such that infinite connectivity (percolation) first occurs.
Social network analysis (SNA) software is software which facilitates quantitative or qualitative analysis of social networks, by describing features of a network either through numerical or visual representation.
In the context of the physical and mathematical theory of percolation, a percolation transition is characterized by a set of universal critical exponents, which describe the fractal properties of the percolating medium at large scales and sufficiently close to the transition. The exponents are universal in the sense that they only depend on the type of percolation model and on the space dimension. They are expected to not depend on microscopic details such as the lattice structure, or whether site or bond percolation is considered. This article deals with the critical exponents of random percolation.
The webgraph describes the directed links between pages of the World Wide Web. A graph, in general, consists of several vertices, some pairs connected by edges. In a directed graph, edges are directed lines or arcs. The webgraph is a directed graph, whose vertices correspond to the pages of the WWW, and a directed edge connects page X to page Y if there exists a hyperlink on page X, referring to page Y.
Cristopher David Moore, known as Cris Moore, is an American computer scientist, mathematician, and physicist. He is resident faculty at the Santa Fe Institute, and was formerly a full professor at the University of New Mexico. He is an elected Fellow of the American Physical Society, the American Mathematical Society, and the American Association for the Advancement of Science.

Scientific collaboration network is a social network where nodes are scientists and links are co-authorships as the latter is one of the most well documented forms of scientific collaboration. It is an undirected, scale-free network where the degree distribution follows a power law with an exponential cutoff – most authors are sparsely connected while a few authors are intensively connected. The network has an assortative nature – hubs tend to link to other hubs and low-degree nodes tend to link to low-degree nodes. Assortativity is not structural, meaning that it is not a consequence of the degree distribution, but it is generated by some process that governs the network’s evolution.
Robustness, the ability to withstand failures and perturbations, is a critical attribute of many complex systems including complex networks.
Aaron Clauset is an American computer scientist who works in the areas of Network Science, Machine Learning, and Complex Systems. He is currently a professor of computer science at the University of Colorado Boulder and is external faculty at the Santa Fe Institute.
References
- ↑ Curriculum vitae, retrieved 2022-12-26.
- ↑ Mark Newman's home page
- ↑ Newman, M. E. J.; Ziff, R. M. (6 Nov 2000). "Efficient Monte Carlo algorithm and high-precision results for percolation". Physical Review Letters. 85 (19): 4014–4107. arXiv: cond-mat/0005264 . Bibcode:2000PhRvL..85.4104N. doi:10.1103/PhysRevLett.85.4104. PMID 11056635.
- ↑ Newman, M.E.J. (29 May 2006). "Power laws, Pareto distributions and Zipf's law". Contemporary Physics. 46: 323–351. arXiv: cond-mat/0412004 . doi:10.1016/j.cities.2012.03.001. S2CID 2871747.
- ↑ Clauset, Aaron; Shazili, Cosma Rohila; Newman, M. E. J. (2 Feb 2009). "Power-law distributions in empirical data". SIAM Review. 51 (4): 661–703. arXiv: 0706.1062 . Bibcode:2009SIAMR..51..661C. doi:10.1137/070710111. S2CID 9155618.
- ↑ Ehrenberg, Rachel (7 November 2012). "Red state, blue state". Science News. The Society for Science and the Public. Retrieved 8 April 2015.
- ↑ "Fifty shades of purple". Physics World. Institute of Physics. 12 November 2012. Retrieved 8 April 2015.
- ↑ Ioannidis, John P. A.; Baas, Jeroen; Klavans, Richard; Boyack, Kevin W. (12 Aug 2019). "A standardized citation metrics author database annotated for scientific field". PLOS Biology. 17 (8): e3000384. doi: 10.1371/journal.pbio.3000384 . PMC 6699798 . PMID 31404057.
- ↑ Newman, Mark E. J. (June 2003). "The structure and function of complex networks". SIAM Review. 45 (2): 167–256. arXiv: cond-mat/0303516 . Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480. S2CID 221278130.
- ↑ "Top institutions in Mathematics". Times Higher Education. 2 June 2011. Retrieved 8 April 2015.