
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations of measure are widely used in quantum physics and physics in general.

In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.
In mathematics, fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set. At the same time, Salii (1965) defined a more general kind of structure called an L-relation, which he studied in an abstract algebraic context. Fuzzy relations, which are now used throughout fuzzy mathematics and have applications in areas such as linguistics, decision-making, and clustering, are special cases of L-relations when L is the unit interval [0, 1].
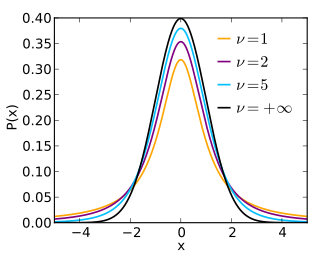
In probability and statistics, Student's t-distribution is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in situations where the sample size is small and the population's standard deviation is unknown. It was developed by English statistician William Sealy Gosset under the pseudonym "Student".
In mathematics, the Kronecker delta is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
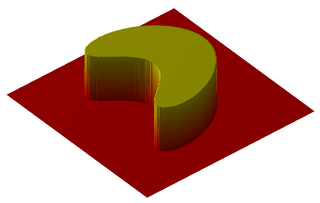
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if A is a subset of some set X, one has if and otherwise, where is a common notation for the indicator function. Other common notations are and
In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus—differentiation and integration. This relationship is commonly characterized in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the Radon–Nikodym derivative, or density, of a measure.
In mathematics, the Radon–Nikodym theorem is a result in measure theory that expresses the relationship between two measures defined on the same measurable space. A measure is a set function that assigns a consistent magnitude to the measurable subsets of a measurable space. Examples of a measure include area and volume, where the subsets are sets of points; or the probability of an event, which is a subset of possible outcomes within a wider probability space.
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure. For a real-valued continuous function f, defined on an interval [a, b] ⊂ R, its total variation on the interval of definition is a measure of the one-dimensional arclength of the curve with parametric equation x ↦ f(x), for x ∈ [a, b]. Functions whose total variation is finite are called functions of bounded variation.

The scaled inverse chi-squared distribution is the distribution for x = 1/s2, where s2 is a sample mean of the squares of ν independent normal random variables that have mean 0 and inverse variance 1/σ2 = τ2. The distribution is therefore parametrised by the two quantities ν and τ2, referred to as the number of chi-squared degrees of freedom and the scaling parameter, respectively.
In mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes. Bernoulli schemes appear naturally in symbolic dynamics, and are thus important in the study of dynamical systems. Many important dynamical systems exhibit a repellor that is the product of the Cantor set and a smooth manifold, and the dynamics on the Cantor set are isomorphic to that of the Bernoulli shift. This is essentially the Markov partition. The term shift is in reference to the shift operator, which may be used to study Bernoulli schemes. The Ornstein isomorphism theorem shows that Bernoulli shifts are isomorphic when their entropy is equal.
In mathematics, signed measure is a generalization of the concept of (positive) measure by allowing the set function to take negative values.
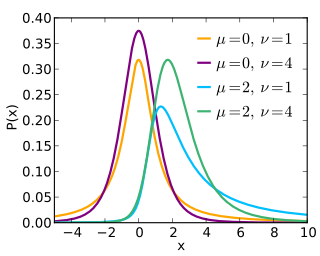
The noncentral t-distribution generalizes Student's t-distribution using a noncentrality parameter. Whereas the central probability distribution describes how a test statistic t is distributed when the difference tested is null, the noncentral distribution describes how t is distributed when the null is false. This leads to its use in statistics, especially calculating statistical power. The noncentral t-distribution is also known as the singly noncentral t-distribution, and in addition to its primary use in statistical inference, is also used in robust modeling for data.
This article discusses how information theory is related to measure theory.
In mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures. In a sense, "disintegration" is the opposite process to the construction of a product measure.
In probability theory, a random measure is a measure-valued random element. Random measures are for example used in the theory of random processes, where they form many important point processes such as Poisson point processes and Cox processes.
f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.

Attempts have been made to describe gauge theories in terms of extended objects such as Wilson loops and holonomies. The loop representation is a quantum hamiltonian representation of gauge theories in terms of loops. The aim of the loop representation in the context of Yang–Mills theories is to avoid the redundancy introduced by Gauss gauge symmetries allowing to work directly in the space of physical states. The idea is well known in the context of lattice Yang–Mills theory. Attempts to explore the continuous loop representation was made by Gambini and Trias for canonical Yang–Mills theory, however there were difficulties as they represented singular objects. As we shall see the loop formalism goes far beyond a simple gauge invariant description, in fact it is the natural geometrical framework to treat gauge theories and quantum gravity in terms of their fundamental physical excitations.

















