
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if for all we have .
In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.
In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes nor odd antiholes. It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 and published by them in 2006.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Paul D. Seymour is the Albert Baldwin Dod Professor of Mathematics at Princeton University. His research interest is in discrete mathematics, especially graph theory. He was responsible for progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, and claw-free graphs. Many of his recent papers are available from his website.

László Lovász is a Hungarian mathematician, best known for his work in combinatorics, for which he was awarded the Wolf Prize and the Knuth Prize in 1999, and the Kyoto Prize in 2010. He was the president of the Hungarian Academy of Sciences between 2014 and 2020. He served as president of the International Mathematical Union between January 1, 2007 and December 31, 2010.
In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

Václav (Vašek) Chvátal (Czech: [ˈvaːtslaf ˈxvaːtal] is a Professor Emeritus in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Quebec, Canada. He has published extensively on topics in graph theory, combinatorics, and combinatorial optimization.
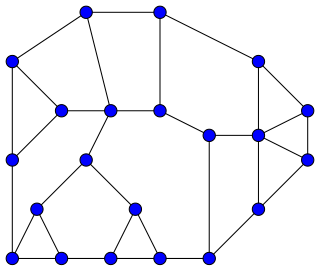
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

Discrete Mathematics is a biweekly peer-reviewed scientific journal in the broad area of discrete mathematics, combinatorics, graph theory, and their applications. It was established in 1971 and is published by North-Holland Publishing Company. It publishes both short notes, full length contributions, as well as survey articles. In addition, the journal publishes a number of special issues each year dedicated to a particular topic. Although originally it published articles in French and German, it now allows only English language articles. The editor-in-chief is Douglas West.

In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Equivalently, these are the graphs in which every maximal independent set has the same size. Well-covered graphs were defined and first studied by Plummer (1970).
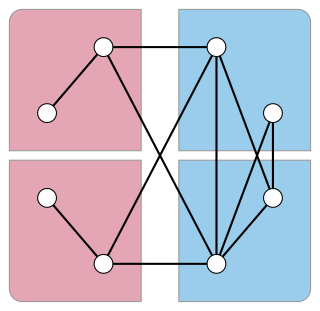
In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:
Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.
Daniel Kráľ is a Czech mathematician and computer scientist who works as a professor of mathematics and computer science at the Masaryk University. His research primarily concerns graph theory and graph algorithms.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.
Deficiency is a concept in graph theory that is used to refine various theorems related to perfect matching in graphs, such as Hall's marriage theorem. Is was first studied by Øystein Ore. A related property is surplus.











