In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842-1850 (Stokes).
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects.
In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.

The Maxwell stress tensor is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
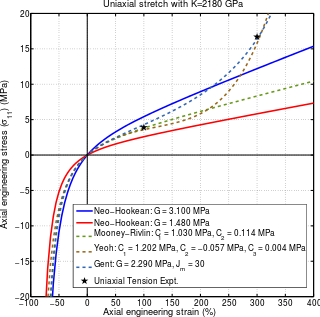
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
The bidomain model is a mathematical model to define the electrical activity of the heart. It consists in a continuum (volume-average) approach in which the cardiac microstructure is defined in terms of muscle fibers grouped in sheets, creating a complex three-dimensional structure with anisotropical properties. Then, to define the electrical activity, two interpenetrating domains are considered, which are the intracellular and extracellular domains, representing respectively the space inside the cells and the region between them.
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one.

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: The line integral of a vector field over a loop is equal to the flux of its curl through the enclosed surface. It is illustrated in the figure, where the direction of positive circulation of the bounding contour ∂Σ, and the direction n of positive flux through the surface Σ, are related by a right-hand-rule. For the right hand the fingers circulate along ∂Σ and the thumb is directed along n.
In the fields of computer vision and image analysis, the scale-invariant feature operator is an algorithm to detect local features in images. The algorithm was published by Förstner et al. in 2009.

In physics, particularly in quantum field theory, the Weyl equation is a relativistic wave equation for describing massless spin-1/2 particles called Weyl fermions. The equation is named after Hermann Weyl. The Weyl fermions are one of the three possible types of elementary fermions, the other two being the Dirac and the Majorana fermions.
For certain applications in linear algebra, it is useful to know properties of the probability distribution of the largest eigenvalue of a finite sum of random matrices. Suppose is a finite sequence of random matrices. Analogous to the well-known Chernoff bound for sums of scalars, a bound on the following is sought for a given parameter t:

In continuum mechanics, objective stress rates are time derivatives of stress that do not depend on the frame of reference. Many constitutive equations are designed in the form of a relation between a stress-rate and a strain-rate. The mechanical response of a material should not depend on the frame of reference. In other words, material constitutive equations should be frame-indifferent (objective). If the stress and strain measures are material quantities then objectivity is automatically satisfied. However, if the quantities are spatial, then the objectivity of the stress-rate is not guaranteed even if the strain-rate is objective.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.

The forward problem of electrocardiology is a computational and mathematical approach to study the electrical activity of the heart through the body surface. The principal aim of this study is to computationally reproduce an electrocardiogram (ECG), which has important clinical relevance to define cardiac pathologies such as ischemia and infarction, or to test pharmaceutical intervention. Given their important functionalities and the relative small invasiveness, the electrocardiography techniques are used quite often as clinical diagnostic tests. Thus, it is natural to proceed to computationally reproduce an ECG, which means to mathematically model the cardiac behaviour inside the body.





















