In incidence geometry, the Moulton plane is an example of an affine plane in which Desargues's theorem does not hold. It is named after the American astronomer Forest Ray Moulton. The points of the Moulton plane are simply the points in the real plane R2 and the lines are the regular lines as well with the exception that for lines with a negative slope, the slope doubles when they pass the y-axis.
The Moulton plane is an incidence structure , where denotes the set of points, the set of lines and the incidence relation "lies on":
is just a formal symbol for an element . It is used to describe vertical lines, which you may think of as lines with an infinitely large slope.
The incidence relation is defined as follows:
For and we have
The Moulton plane is an affine plane in which Desargues' theorem does not hold. [1] The associated projective plane is consequently non-desarguesian as well. This means that there are projective planes not isomorphic to for any (skew) field F. Here is the projective plane determined by a 3-dimensional vector space over the (skew) field F.
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect in one and only one point.
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seems to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.
Projective geometry is a topic in mathematics. It is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.
In mathematics, affine geometry is what remains of Euclidean geometry when not using the metric notions of distance and angle.
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.
In geometry, a striking feature of projective planes is the symmetry of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this concept. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.
In geometry, an affine plane is a system of points and lines that satisfy the following axioms:
The notion of line or straight line was introduced by ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects. Until the 17th century, lines were defined as the "[…] first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width. […] The straight line is that which is equally extended between its points."
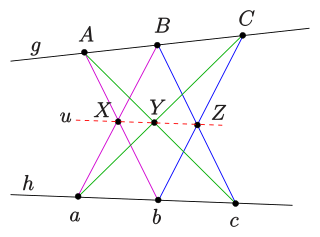
In mathematics, Pappus's hexagon theorem states that
In mathematics, Hilbert's fourth problem in the 1900 Hilbert problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.
In mathematics, a translation plane is a particular kind of projective plane. Almost all non-Desarguesian planes are either translation planes or are related to this type of incidence structure.
In projective geometry an oval is a circle-like pointset (curve) in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.
In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension d ≥ 3. Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid are:
In mathematics, a Minkowski plane is one of the Benz planes.
In projective geometry, an intersection theorem or incidence theorem is a statement concerning an incidence structure – consisting of points, lines, and possibly higher-dimensional objects and their incidences – together with a pair of objects A and B. The "theorem" states that, whenever a set of objects satisfies the incidences, then the objects A and B must also be incident. An intersection theorem is not necessarily true in all projective geometries; it is a property that some geometries satisfy but others don't.
In mathematics, a Benz plane is a type of 2-dimensional geometrical structure, named after the German mathematician Walter Benz. The term was applied to a group of objects that arise from a common axiomatization of certain structures and split into three families, which were introduced separately: Möbius planes, Laguerre planes, and Minkowski planes.
In mathematics, a Laguerre plane is one of the Benz planes: the Möbius plane, Laguerre plane and Minkowski plane, named after the French mathematician Edmond Nicolas Laguerre.
In mathematics, a Möbius plane is one of the Benz planes: Möbius plane, Laguerre plane and Minkowski plane. The classical example is based on the geometry of lines and circles in the real affine plane.
Topological geometry deals with incidence structures consisting of a point set and a family of subsets of called lines or circles etc. such that both and carry a topology and all geometric operations like joining points by a line or intersecting lines are continuous. As in the case of topological groups, many deeper results require the point space to be (locally) compact and connected. This generalizes the observation that the line joining two distinct points in the Euclidean plane depends continuously on the pair of points and the intersection point of two lines is a continuous function of these lines.
