Multicategory

Last updated May 27, 2024

In mathematics (especially category theory), a multicategory is a generalization of the concept of category that allows morphisms of multiple arity. If morphisms in a category are viewed as analogous to functions, then morphisms in a multicategory are analogous to functions of several variables. Multicategories are also sometimes called operads, or colored operads.

Definition

A (non-symmetric) multicategory consists of

a collection (often a proper class) of objects;
for every finite sequence $(X_{i})_{i\in [n]}$ of objects ( $[n]=\{0,1,2,...,n\}$ ) and every object Y, a set of morphisms from $(X_{i})_{i\in n}$ to Y; and
for every object X, a special identity morphism (with n = 1) from X to X.

Additionally, there are composition operations: Given a sequence of sequences $((X_{ij})_{i\in n_{j}})_{j\in m}$ of objects, a sequence $(Y_{j})_{j\in m}$ of objects, and an object Z: if

for each $j\in m$ , f_j is a morphism from $(X_{ij})_{i\in n_{j}}$ to Y_j; and
g is a morphism from $(Y_{j})_{j\in m}$ to Z:

then there is a composite morphism $g(f_{j})_{j\in m}$ from $(X_{ij})_{i\in n_{j},j\in m}$ to Z. This must satisfy certain axioms:

If m = 1, Z = Y₀, and g is the identity morphism for Y₀, then g(f₀) = f₀;
if for each $j\in m$ , n_j = 1, $X_{0j}=Y_{j}$ , and f_j is the identity morphism for Y_j, then $g(f_{j})_{j\in m}=g$ ; and
an associativity condition: if for each $j\in m$ and $i\in n_{j}$ , $e_{ij}$ is a morphism from $(W_{hij})_{h\in o_{ij}}$ to $X_{ij}$ , then $g\left(f_{j}(e_{ij})_{i\in n_{j}}\right)_{j\in m}=g(f_{j})_{j\in m}(e_{ij})_{i\in n_{j},j\in m}$ are identical morphisms from $(W_{hij})_{h\in o_{ij},i\in n_{j},j\in m}$ to Z.

Comcategories

A comcategory (co-multi-category) is a totally ordered set O of objects, a set A of multiarrows with two functions

$\mathrm {head} :A\rightarrow O,$

$\mathrm {ground} :A\rightarrow O^{\%},$

where O^% is the set of all finite ordered sequences of elements of O. The dual image of a multiarrow f may be summarized

$f:\mathrm {head} (f)\Leftarrow \mathrm {ground} (f).$

A comcategory C also has a multiproduct with the usual character of a composition operation. C is said to be associative if there holds a multiproduct axiom in relation to this operator.

Any multicategory, symmetric or non-symmetric, together with a total-ordering of the object set, can be made into an equivalent comcategory.

A multiorder is a comcategory satisfying the following conditions.

There is at most one multiarrow with given head and ground.
Each object x has a unit multiarrow.
A multiarrow is a unit if its ground has one entry.

Multiorders are a generalization of partial orders (posets), and were first introduced (in passing) by Tom Leinster.^[1]

Examples

There is a multicategory whose objects are (small) sets, where a morphism from the sets X₁, X₂, ..., and X_n to the set Y is an n-ary function, that is a function from the Cartesian product X₁ × X₂ × ... × X_n to Y.

There is a multicategory whose objects are vector spaces (over the rational numbers, say), where a morphism from the vector spaces X₁, X₂, ..., and X_n to the vector space Y is a multilinear operator, that is a linear transformation from the tensor product X₁ ⊗ X₂ ⊗ ... ⊗ X_n to Y.

More generally, given any monoidal category C, there is a multicategory whose objects are objects of C, where a morphism from the C-objects X₁, X₂, ..., and X_n to the C-object Y is a C-morphism from the monoidal product of X₁, X₂, ..., and X_n to Y.

An operad is a multicategory with one unique object; except in degenerate cases, such a multicategory does not come from a monoidal category.

Examples of multiorders include pointed multisets(sequence A262671 in the OEIS ), integer partitions(sequence A063834 in the OEIS ), and combinatory separations(sequence A269134 in the OEIS ). The triangles (or compositions) of any multiorder are morphisms of a (not necessarily associative) category of contractions and a comcategory of decompositions. The contraction category for the multiorder of multimin partitions(sequence A255397 in the OEIS ) is the simplest known category of multisets.^[2]

Applications

Multicategories are often incorrectly considered to belong to higher category theory, as their original application was the observation that the operators and identities satisfied by higher categories are the objects and multiarrows of a multicategory. The study of n-categories was in turn motivated by applications in algebraic topology and attempts to describe the homotopy theory of higher dimensional manifolds. However it has mostly grown out of this motivation and is now also considered to be part of pure mathematics.

The correspondence between contractions and decompositions of triangles in a multiorder allows one to construct an associative algebra called its incidence algebra. Any element that is nonzero on all unit arrows has a compositional inverse, and the Möbius function of a multiorder is defined as the compositional inverse of the zeta function (constant-one) in its incidence algebra.

History

Multicategories were first introduced under that name by Jim Lambek in "Deductive systems and categories II" (1969)^[3] He mentions (p. 108) that he was "told that multicategories have also been studied by [Jean] Benabou and [Pierre] Cartier", and indeed Leinster opines that "the idea might have occurred to anyone who knew what both a category and a multilinear map were".^[1]^: 63

Related Research Articles

In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.

In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:

Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular groups as the object of study, in universal algebra one takes the class of groups as an object of study.

In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.

In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.

Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.

In algebraic geometry, an affine algebraic set is the set of the common zeros over an algebraically closed field $k$ of some family of polynomials in the polynomial ring $An affine variety or affine algebraic variety, is an affine algebraic set such that the ideal generated by the defining polynomials is prime.$

In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antihomomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations.

In mathematics, a scheme is a mathematical structure that enlarges the notion of algebraic variety in several ways, such as taking account of multiplicities and allowing "varieties" defined over any commutative ring.

In algebraic geometry, motives is a theory proposed by Alexander Grothendieck in the 1960s to unify the vast array of similarly behaved cohomology theories such as singular cohomology, de Rham cohomology, etale cohomology, and crystalline cohomology. Philosophically, a "motif" is the "cohomology essence" of a variety.

In mathematics, algebraic geometry and analytic geometry are two closely related subjects. While algebraic geometry studies algebraic varieties, analytic geometry deals with complex manifolds and the more general analytic spaces defined locally by the vanishing of analytic functions of several complex variables. The deep relation between these subjects has numerous applications in which algebraic techniques are applied to analytic spaces and analytic techniques to algebraic varieties.

In mathematics, an algebraic stack is a vast generalization of algebraic spaces, or schemes, which are foundational for studying moduli theory. Many moduli spaces are constructed using techniques specific to algebraic stacks, such as Artin's representability theorem, which is used to construct the moduli space of pointed algebraic curves $and the moduli stack of elliptic curves. Originally, they were introduced by Alexander Grothendieck to keep track of automorphisms on moduli spaces, a technique which allows for treating these moduli spaces as if their underlying schemes or algebraic spaces are smooth. After Grothendieck developed the general theory of descent, and Giraud the general theory of stacks, the notion of algebraic stacks was defined by Michael Artin.$

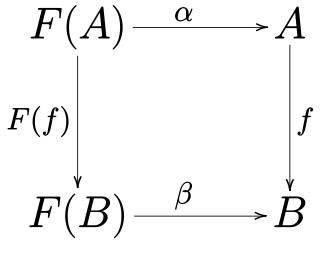
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.

This is a glossary of properties and concepts in category theory in mathematics.

In mathematics, algebraic spaces form a generalization of the schemes of algebraic geometry, introduced by Michael Artin for use in deformation theory. Intuitively, schemes are given by gluing together affine schemes using the Zariski topology, while algebraic spaces are given by gluing together affine schemes using the finer étale topology. Alternatively one can think of schemes as being locally isomorphic to affine schemes in the Zariski topology, while algebraic spaces are locally isomorphic to affine schemes in the étale topology.

In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad $, one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.$

In category theory, a branch of mathematics, a PROP is a symmetric strict monoidal category whose objects are the natural numbers n identified with the finite sets $and whose tensor product is given on objects by the addition on numbers. Because of “symmetric”, for each n, the symmetric group on n letters is given as a subgroup of the automorphism group of n . The name PROP is an abbreviation of "PROduct and Permutation category".$

In category theory, a branch of mathematics, the center is a variant of the notion of the center of a monoid, group, or ring to a category.

In category theory, a branch of mathematics, a rigid category is a monoidal category where every object is rigid, that is, has a dual X^* and a morphism 1 → X ⊗ X^* satisfying natural conditions. The category is called right rigid or left rigid according to whether it has right duals or left duals. They were first defined by Neantro Saavedra Rivano in his thesis on Tannakian categories.

References

1 2 Tom Leinster (2004). Higher Operads, Higher Categories. Cambridge University Press. arXiv: math/0305049 . Bibcode:2004hohc.book.....L., Example 2.1.7, page 37
↑ Wiseman, Gus. "Comcategories and Multiorders". Google Docs. Retrieved 9 May 2016.
↑ .Lambek, Joachim (1969). "Deductive systems and categories II. Standard constructions and closed categories". Lecture Notes in Mathematics. Vol. 86. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 76–122. doi:10.1007/bfb0079385. ISBN 978-3-540-04605-9. ISSN 0075-8434.

Garner, Richard (2008). "Polycategories via pseudo-distributive laws". Advances in Mathematics . 218 (3): 781–827. arXiv: math/0606735 . doi: 10.1016/j.aim.2008.02.001 . S2CID 17057235.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[leinster-1] 1 2 Tom Leinster (2004). Higher Operads, Higher Categories. Cambridge University Press. arXiv: math/0305049 . Bibcode:2004hohc.book.....L., Example 2.1.7, page 37

[2] Wiseman, Gus. "Comcategories and Multiorders". Google Docs. Retrieved 9 May 2016.

[Lambek1969-3] .Lambek, Joachim (1969). "Deductive systems and categories II. Standard constructions and closed categories". Lecture Notes in Mathematics. Vol. 86. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 76–122. doi:10.1007/bfb0079385. ISBN 978-3-540-04605-9. ISSN 0075-8434.

[1]

[2]

[3]