Multifactor dimensionality reduction

Last updated

Multifactor dimensionality reduction (MDR) is a statistical approach, also used in machine learning automatic approaches, [1] for detecting and characterizing combinations of attributes or independent variables that interact to influence a dependent or class variable. [2] [3] [4] [5] [6] [7] [8] MDR was designed specifically to identify nonadditive interactions among discrete variables that influence a binary outcome and is considered a nonparametric and model-free alternative to traditional statistical methods such as logistic regression.

Contents

The basis of the MDR method is a constructive induction or feature engineering algorithm that converts two or more variables or attributes to a single attribute. [9] This process of constructing a new attribute changes the representation space of the data. [10] The end goal is to create or discover a representation that facilitates the detection of nonlinear [ disambiguation needed ] or nonadditive interactions among the attributes such that prediction of the class variable is improved over that of the original representation of the data.

Illustrative example

Consider the following simple example using the exclusive OR (XOR) function. XOR is a logical operator that is commonly used in data mining and machine learning as an example of a function that is not linearly separable. The table below represents a simple dataset where the relationship between the attributes (X1 and X2) and the class variable (Y) is defined by the XOR function such that Y = X1 XOR X2.

Table 1

X1X2Y
000
011
101
110

A machine learning algorithm would need to discover or approximate the XOR function in order to accurately predict Y using information about X1 and X2. An alternative strategy would be to first change the representation of the data using constructive induction to facilitate predictive modeling. The MDR algorithm would change the representation of the data (X1 and X2) in the following manner. MDR starts by selecting two attributes. In this simple example, X1 and X2 are selected. Each combination of values for X1 and X2 are examined and the number of times Y=1 and/or Y=0 is counted. In this simple example, Y=1 occurs zero times and Y=0 occurs once for the combination of X1=0 and X2=0. With MDR, the ratio of these counts is computed and compared to a fixed threshold. Here, the ratio of counts is 0/1 which is less than our fixed threshold of 1. Since 0/1 < 1 we encode a new attribute (Z) as a 0. When the ratio is greater than one we encode Z as a 1. This process is repeated for all unique combinations of values for X1 and X2. Table 2 illustrates our new transformation of the data.

Table 2

ZY
00
11
11
00

The machine learning algorithm now has much less work to do to find a good predictive function. In fact, in this very simple example, the function Y = Z has a classification accuracy of 1. A nice feature of constructive induction methods such as MDR is the ability to use any data mining or machine learning method to analyze the new representation of the data. Decision trees, neural networks, or a naive Bayes classifier could be used in combination with measures of model quality such as balanced accuracy [11] [12] and mutual information. [13]

Machine learning with MDR

As illustrated above, the basic constructive induction algorithm in MDR is very simple. However, its implementation for mining patterns from real data can be computationally complex. As with any machine learning algorithm there is always concern about overfitting. That is, machine learning algorithms are good at finding patterns in completely random data. It is often difficult to determine whether a reported pattern is an important signal or just chance. One approach is to estimate the generalizability of a model to independent datasets using methods such as cross-validation. [14] [15] [16] [17] Models that describe random data typically don't generalize. Another approach is to generate many random permutations of the data to see what the data mining algorithm finds when given the chance to overfit. Permutation testing makes it possible to generate an empirical p-value for the result. [18] [19] [20] [21] Replication in independent data may also provide evidence for an MDR model but can be sensitive to difference in the data sets. [22] [23] These approaches have all been shown to be useful for choosing and evaluating MDR models. An important step in a machine learning exercise is interpretation. Several approaches have been used with MDR including entropy analysis [9] [24] and pathway analysis. [25] [26] Tips and approaches for using MDR to model gene-gene interactions have been reviewed. [7] [27]

Extensions to MDR

Numerous extensions to MDR have been introduced. These include family-based methods, [28] [29] [30] fuzzy methods, [31] covariate adjustment, [32] odds ratios, [33] risk scores, [34] survival methods, [35] [36] robust methods, [37] methods for quantitative traits, [38] [39] and many others.

Applications of MDR

MDR has mostly been applied to detecting gene-gene interactions or epistasis in genetic studies of common human diseases such as atrial fibrillation, [40] [41] autism, [42] bladder cancer, [43] [44] [45] breast cancer, [46] cardiovascular disease, [14] hypertension, [47] [48] [49] obesity, [50] [51] pancreatic cancer, [52] prostate cancer [53] [54] [55] and tuberculosis. [56] It has also been applied to other biomedical problems such as the genetic analysis of pharmacology outcomes. [57] [58] [59] A central challenge is the scaling of MDR to big data such as that from genome-wide association studies (GWAS). [60] Several approaches have been used. One approach is to filter the features prior to MDR analysis. [61] This can be done using biological knowledge through tools such as BioFilter. [62] It can also be done using computational tools such as ReliefF. [63] Another approach is to use stochastic search algorithms such as genetic programming to explore the search space of feature combinations. [64] Yet another approach is a brute-force search using high-performance computing. [65] [66] [67]

Implementations

See also

Related Research Articles

<span class="mw-page-title-main">Bioinformatics</span> Computational analysis of large, complex sets of biological data

Bioinformatics is an interdisciplinary field of science that develops methods and software tools for understanding biological data, especially when the data sets are large and complex. Bioinformatics uses biology, chemistry, physics, computer science, computer programming, information engineering, mathematics and statistics to analyze and interpret biological data. The subsequent process of analyzing and interpreting data is referred to as computational biology.

<span class="mw-page-title-main">Phenotype</span> Composite of the organisms observable characteristics or traits

In genetics, the phenotype is the set of observable characteristics or traits of an organism. The term covers the organism's morphology, its developmental processes, its biochemical and physiological properties, its behavior, and the products of behavior. An organism's phenotype results from two basic factors: the expression of an organism's genetic code and the influence of environmental factors. Both factors may interact, further affecting the phenotype. When two or more clearly different phenotypes exist in the same population of a species, the species is called polymorphic. A well-documented example of polymorphism is Labrador Retriever coloring; while the coat color depends on many genes, it is clearly seen in the environment as yellow, black, and brown. Richard Dawkins in 1978 and then again in his 1982 book The Extended Phenotype suggested that one can regard bird nests and other built structures such as caddisfly larva cases and beaver dams as "extended phenotypes".

<span class="mw-page-title-main">DNA microarray</span> Collection of microscopic DNA spots attached to a solid surface

A DNA microarray is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome. Each DNA spot contains picomoles of a specific DNA sequence, known as probes. These can be a short section of a gene or other DNA element that are used to hybridize a cDNA or cRNA sample under high-stringency conditions. Probe-target hybridization is usually detected and quantified by detection of fluorophore-, silver-, or chemiluminescence-labeled targets to determine relative abundance of nucleic acid sequences in the target. The original nucleic acid arrays were macro arrays approximately 9 cm × 12 cm and the first computerized image based analysis was published in 1981. It was invented by Patrick O. Brown. An example of its application is in SNPs arrays for polymorphisms in cardiovascular diseases, cancer, pathogens and GWAS analysis. It is also used for the identification of structural variations and the measurement of gene expression.

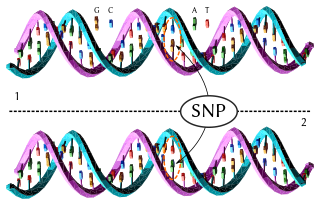
<span class="mw-page-title-main">Single-nucleotide polymorphism</span> Single nucleotide in genomic DNA at which different sequence alternatives exist

In genetics and bioinformatics, a single-nucleotide polymorphism is a germline substitution of a single nucleotide at a specific position in the genome. Although certain definitions require the substitution to be present in a sufficiently large fraction of the population, many publications do not apply such a frequency threshold.

<span class="mw-page-title-main">Functional genomics</span> Field of molecular biology

Functional genomics is a field of molecular biology that attempts to describe gene functions and interactions. Functional genomics make use of the vast data generated by genomic and transcriptomic projects. Functional genomics focuses on the dynamic aspects such as gene transcription, translation, regulation of gene expression and protein–protein interactions, as opposed to the static aspects of the genomic information such as DNA sequence or structures. A key characteristic of functional genomics studies is their genome-wide approach to these questions, generally involving high-throughput methods rather than a more traditional "candidate-gene" approach.

<span class="mw-page-title-main">Interactome</span> Complete set of molecular interactions in a biological cell

In molecular biology, an interactome is the whole set of molecular interactions in a particular cell. The term specifically refers to physical interactions among molecules but can also describe sets of indirect interactions among genes.

Genetic architecture is the underlying genetic basis of a phenotypic trait and its variational properties. Phenotypic variation for quantitative traits is, at the most basic level, the result of the segregation of alleles at quantitative trait loci (QTL). Environmental factors and other external influences can also play a role in phenotypic variation. Genetic architecture is a broad term that can be described for any given individual based on information regarding gene and allele number, the distribution of allelic and mutational effects, and patterns of pleiotropy, dominance, and epistasis.

<span class="mw-page-title-main">Protein–protein interaction</span> Physical interactions and constructions between multiple proteins

Protein–protein interactions (PPIs) are physical contacts of high specificity established between two or more protein molecules as a result of biochemical events steered by interactions that include electrostatic forces, hydrogen bonding and the hydrophobic effect. Many are physical contacts with molecular associations between chains that occur in a cell or in a living organism in a specific biomolecular context.

Biomedical text mining refers to the methods and study of how text mining may be applied to texts and literature of the biomedical domain. As a field of research, biomedical text mining incorporates ideas from natural language processing, bioinformatics, medical informatics and computational linguistics. The strategies in this field have been applied to the biomedical literature available through services such as PubMed.

<span class="mw-page-title-main">Genome-wide association study</span> Study of genetic variants in different individuals

In genomics, a genome-wide association study, is an observational study of a genome-wide set of genetic variants in different individuals to see if any variant is associated with a trait. GWA studies typically focus on associations between single-nucleotide polymorphisms (SNPs) and traits like major human diseases, but can equally be applied to any other genetic variants and any other organisms.

<span class="mw-page-title-main">Chromosome conformation capture</span>

Chromosome conformation capture techniques are a set of molecular biology methods used to analyze the spatial organization of chromatin in a cell. These methods quantify the number of interactions between genomic loci that are nearby in 3-D space, but may be separated by many nucleotides in the linear genome. Such interactions may result from biological functions, such as promoter-enhancer interactions, or from random polymer looping, where undirected physical motion of chromatin causes loci to collide. Interaction frequencies may be analyzed directly, or they may be converted to distances and used to reconstruct 3-D structures.

<span class="mw-page-title-main">Jason H. Moore</span>

Jason H. Moore is a translational bioinformatics scientist, biomedical informatician, and human geneticist, the Edward Rose Professor of Informatics and Director of the Institute for Biomedical Informatics at the Perelman School of Medicine at the University of Pennsylvania, where he is also Senior Associate Dean for Informatics and Director of the Division of Informatics in the Department of Biostatistics, Epidemiology, and Informatics.

Relief is an algorithm developed by Kira and Rendell in 1992 that takes a filter-method approach to feature selection that is notably sensitive to feature interactions. It was originally designed for application to binary classification problems with discrete or numerical features. Relief calculates a feature score for each feature which can then be applied to rank and select top scoring features for feature selection. Alternatively, these scores may be applied as feature weights to guide downstream modeling. Relief feature scoring is based on the identification of feature value differences between nearest neighbor instance pairs. If a feature value difference is observed in a neighboring instance pair with the same class, the feature score decreases. Alternatively, if a feature value difference is observed in a neighboring instance pair with different class values, the feature score increases. The original Relief algorithm has since inspired a family of Relief-based feature selection algorithms (RBAs), including the ReliefF algorithm. Beyond the original Relief algorithm, RBAs have been adapted to (1) perform more reliably in noisy problems, (2) generalize to multi-class problems (3) generalize to numerical outcome problems, and (4) to make them robust to incomplete data.

Flow cytometry bioinformatics is the application of bioinformatics to flow cytometry data, which involves storing, retrieving, organizing and analyzing flow cytometry data using extensive computational resources and tools. Flow cytometry bioinformatics requires extensive use of and contributes to the development of techniques from computational statistics and machine learning. Flow cytometry and related methods allow the quantification of multiple independent biomarkers on large numbers of single cells. The rapid growth in the multidimensionality and throughput of flow cytometry data, particularly in the 2000s, has led to the creation of a variety of computational analysis methods, data standards, and public databases for the sharing of results.

Genetic reductionism is the belief that understanding genes is sufficient to understand all aspects of human behavior. It is a specific form of reductionism and of biological determinism, based on a perspective which defines genes as distinct units of information with consistent properties. It also covers attempts to define specific phenomena in exclusively genetic terms, as in the case of the "warrior gene".

Single nucleotide polymorphism annotation is the process of predicting the effect or function of an individual SNP using SNP annotation tools. In SNP annotation the biological information is extracted, collected and displayed in a clear form amenable to query. SNP functional annotation is typically performed based on the available information on nucleic acid and protein sequences.

<span class="mw-page-title-main">Epistasis</span> Dependence of a gene mutations phenotype on mutations in other genes

Epistasis is a phenomenon in genetics in which the effect of a gene mutation is dependent on the presence or absence of mutations in one or more other genes, respectively termed modifier genes. In other words, the effect of the mutation is dependent on the genetic background in which it appears. Epistatic mutations therefore have different effects on their own than when they occur together. Originally, the term epistasis specifically meant that the effect of a gene variant is masked by that of different gene.

Perturb-seq refers to a high-throughput method of performing single cell RNA sequencing (scRNA-seq) on pooled genetic perturbation screens. Perturb-seq combines multiplexed CRISPR mediated gene inactivations with single cell RNA sequencing to assess comprehensive gene expression phenotypes for each perturbation. Inferring a gene’s function by applying genetic perturbations to knock down or knock out a gene and studying the resulting phenotype is known as reverse genetics. Perturb-seq is a reverse genetics approach that allows for the investigation of phenotypes at the level of the transcriptome, to elucidate gene functions in many cells, in a massively parallel fashion.

Machine learning in bioinformatics is the application of machine learning algorithms to bioinformatics, including genomics, proteomics, microarrays, systems biology, evolution, and text mining.

References

  1. ↑ McKinney, Brett A.; Reif, David M.; Ritchie, Marylyn D.; Moore, Jason H. (1 January 2006). "Machine learning for detecting gene-gene interactions: a review". Applied Bioinformatics. 5 (2): 77–88. doi:10.2165/00822942-200605020-00002. ISSN   1175-5636. PMC   3244050 . PMID   16722772.
  2. ↑ Ritchie, Marylyn D.; Hahn, Lance W.; Roodi, Nady; Bailey, L. Renee; Dupont, William D.; Parl, Fritz F.; Moore, Jason H. (1 July 2001). "Multifactor-Dimensionality Reduction Reveals High-Order Interactions among Estrogen-Metabolism Genes in Sporadic Breast Cancer". The American Journal of Human Genetics. 69 (1): 138–147. doi:10.1086/321276. ISSN   0002-9297. PMC   1226028 . PMID   11404819.
  3. ↑ Ritchie, Marylyn D.; Hahn, Lance W.; Moore, Jason H. (1 February 2003). "Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity". Genetic Epidemiology. 24 (2): 150–157. doi:10.1002/gepi.10218. ISSN   1098-2272. PMID   12548676. S2CID   6335612.
  4. ↑ Hahn, L. W.; Ritchie, M. D.; Moore, J. H. (12 February 2003). "Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions". Bioinformatics. 19 (3): 376–382. doi: 10.1093/bioinformatics/btf869 . ISSN   1367-4803. PMID   12584123.
  5. ↑ W., Hahn, Lance; H., Moore, Jason (1 January 2004). "Ideal Discrimination of Discrete Clinical Endpoints Using Multilocus Genotypes". In Silico Biology. 4 (2): 183–194. ISSN   1386-6338. PMID   15107022.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  6. ↑ Moore, Jason H. (1 November 2004). "Computational analysis of gene-gene interactions using multifactor dimensionality reduction". Expert Review of Molecular Diagnostics. 4 (6): 795–803. doi:10.1586/14737159.4.6.795. ISSN   1473-7159. PMID   15525222. S2CID   26324399.
  7. 1 2 Moore, JasonH.; Andrews, PeterC. (1 January 2015). "Epistasis Analysis Using Multifactor Dimensionality Reduction". In Moore, Jason H.; Williams, Scott M. (eds.). Epistasis. Methods in Molecular Biology. Vol. 1253. Springer New York. pp. 301–314. doi:10.1007/978-1-4939-2155-3_16. ISBN   9781493921546. PMID   25403539.
  8. ↑ Moore, Jason H. (1 January 2010). "Detecting, characterizing, and interpreting nonlinear gene-gene interactions using multifactor dimensionality reduction". Advances in Genetics. 72: 101–116. doi:10.1016/B978-0-12-380862-2.00005-9. ISBN   978-0-12-380862-2. ISSN   0065-2660. PMID   21029850.
  9. 1 2 Moore, Jason H.; Gilbert, Joshua C.; Tsai, Chia-Ti; Chiang, Fu-Tien; Holden, Todd; Barney, Nate; White, Bill C. (21 July 2006). "A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility". Journal of Theoretical Biology. 241 (2): 252–261. doi:10.1016/j.jtbi.2005.11.036. PMID   16457852.
  10. ↑ Michalski, R (February 1983). "A theory and methodology of inductive learning". Artificial Intelligence. 20 (2): 111–161. doi:10.1016/0004-3702(83)90016-4.
  11. ↑ Velez, Digna R.; White, Bill C.; Motsinger, Alison A.; Bush, William S.; Ritchie, Marylyn D.; Williams, Scott M.; Moore, Jason H. (1 May 2007). "A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction". Genetic Epidemiology. 31 (4): 306–315. doi:10.1002/gepi.20211. ISSN   0741-0395. PMID   17323372. S2CID   28156181.
  12. ↑ Namkung, Junghyun; Kim, Kyunga; Yi, Sungon; Chung, Wonil; Kwon, Min-Seok; Park, Taesung (1 February 2009). "New evaluation measures for multifactor dimensionality reduction classifiers in gene-gene interaction analysis". Bioinformatics. 25 (3): 338–345. doi: 10.1093/bioinformatics/btn629 . ISSN   1367-4811. PMID   19164302.
  13. ↑ Bush, William S.; Edwards, Todd L.; Dudek, Scott M.; McKinney, Brett A.; Ritchie, Marylyn D. (1 January 2008). "Alternative contingency table measures improve the power and detection of multifactor dimensionality reduction". BMC Bioinformatics. 9: 238. doi: 10.1186/1471-2105-9-238 . ISSN   1471-2105. PMC   2412877 . PMID   18485205.
  14. 1 2 Coffey, Christopher S.; Hebert, Patricia R.; Ritchie, Marylyn D.; Krumholz, Harlan M.; Gaziano, J. Michael; Ridker, Paul M.; Brown, Nancy J.; Vaughan, Douglas E.; Moore, Jason H. (1 January 2004). "An application of conditional logistic regression and multifactor dimensionality reduction for detecting gene-gene Interactions on risk of myocardial infarction: The importance of model validation". BMC Bioinformatics. 5: 49. doi: 10.1186/1471-2105-5-49 . ISSN   1471-2105. PMC   419697 . PMID   15119966.
  15. ↑ Motsinger, Alison A.; Ritchie, Marylyn D. (1 September 2006). "The effect of reduction in cross-validation intervals on the performance of multifactor dimensionality reduction". Genetic Epidemiology. 30 (6): 546–555. doi:10.1002/gepi.20166. ISSN   1098-2272. PMID   16800004. S2CID   20573232.
  16. ↑ Gory, Jeffrey J.; Sweeney, Holly C.; Reif, David M.; Motsinger-Reif, Alison A. (5 November 2012). "A comparison of internal model validation methods for multifactor dimensionality reduction in the case of genetic heterogeneity". BMC Research Notes. 5: 623. doi: 10.1186/1756-0500-5-623 . ISSN   1756-0500. PMC   3599301 . PMID   23126544.
  17. ↑ Winham, Stacey J.; Slater, Andrew J.; Motsinger-Reif, Alison A. (22 July 2010). "A comparison of internal validation techniques for multifactor dimensionality reduction". BMC Bioinformatics. 11: 394. doi: 10.1186/1471-2105-11-394 . ISSN   1471-2105. PMC   2920275 . PMID   20650002.
  18. ↑ Pattin, Kristine A.; White, Bill C.; Barney, Nate; Gui, Jiang; Nelson, Heather H.; Kelsey, Karl T.; Andrew, Angeline S.; Karagas, Margaret R.; Moore, Jason H. (1 January 2009). "A computationally efficient hypothesis testing method for epistasis analysis using multifactor dimensionality reduction". Genetic Epidemiology. 33 (1): 87–94. doi:10.1002/gepi.20360. ISSN   1098-2272. PMC   2700860 . PMID   18671250.
  19. ↑ Greene, Casey S.; Himmelstein, Daniel S.; Nelson, Heather H.; Kelsey, Karl T.; Williams, Scott M.; Andrew, Angeline S.; Karagas, Margaret R.; Moore, Jason H. (1 October 2009). "Enabling personal genomics with an explicit test of epistasis". Biocomputing 2010: Pacific Symposium on Biocomputing. World Scientific. pp. 327–336. doi:10.1142/9789814295291_0035. ISBN   9789814299473. PMC   2916690 . PMID   19908385.
  20. ↑ Dai, Hongying; Bhandary, Madhusudan; Becker, Mara; Leeder, J. Steven; Gaedigk, Roger; Motsinger-Reif, Alison A. (22 May 2012). "Global tests of P-values for multifactor dimensionality reduction models in selection of optimal number of target genes". BioData Mining. 5 (1): 3. doi: 10.1186/1756-0381-5-3 . ISSN   1756-0381. PMC   3508622 . PMID   22616673.
  21. ↑ Motsinger-Reif, Alison A. (30 December 2008). "The effect of alternative permutation testing strategies on the performance of multifactor dimensionality reduction". BMC Research Notes. 1: 139. doi: 10.1186/1756-0500-1-139 . ISSN   1756-0500. PMC   2631601 . PMID   19116021.
  22. ↑ Greene, Casey S.; Penrod, Nadia M.; Williams, Scott M.; Moore, Jason H. (2 June 2009). "Failure to Replicate a Genetic Association May Provide Important Clues About Genetic Architecture". PLOS ONE. 4 (6): e5639. Bibcode:2009PLoSO...4.5639G. doi: 10.1371/journal.pone.0005639 . ISSN   1932-6203. PMC   2685469 . PMID   19503614.
  23. ↑ Piette, Elizabeth R.; Moore, Jason H. (19 April 2017). "Improving the Reproducibility of Genetic Association Results Using Genotype Resampling Methods". Applications of Evolutionary Computation. Lecture Notes in Computer Science. Vol. 10199. pp. 96–108. doi:10.1007/978-3-319-55849-3_7. ISBN   978-3-319-55848-6.
  24. ↑ Moore, Jason H.; Hu, Ting (1 January 2015). "Epistasis Analysis Using Information Theory". Epistasis. Methods in Molecular Biology. Vol. 1253. pp. 257–268. doi:10.1007/978-1-4939-2155-3_13. ISBN   978-1-4939-2154-6. ISSN   1940-6029. PMID   25403536.
  25. ↑ Kim, Nora Chung; Andrews, Peter C.; Asselbergs, Folkert W.; Frost, H. Robert; Williams, Scott M.; Harris, Brent T.; Read, Cynthia; Askland, Kathleen D.; Moore, Jason H. (28 July 2012). "Gene ontology analysis of pairwise genetic associations in two genome-wide studies of sporadic ALS". BioData Mining. 5 (1): 9. doi: 10.1186/1756-0381-5-9 . ISSN   1756-0381. PMC   3463436 . PMID   22839596.
  26. ↑ Cheng, Samantha; Andrew, Angeline S.; Andrews, Peter C.; Moore, Jason H. (1 January 2016). "Complex systems analysis of bladder cancer susceptibility reveals a role for decarboxylase activity in two genome-wide association studies". BioData Mining. 9: 40. doi: 10.1186/s13040-016-0119-z . PMC   5154053 . PMID   27999618.
  27. ↑ Gola, Damian; Mahachie John, Jestinah M.; van Steen, Kristel; König, Inke R. (1 March 2016). "A roadmap to multifactor dimensionality reduction methods". Briefings in Bioinformatics. 17 (2): 293–308. doi:10.1093/bib/bbv038. ISSN   1477-4054. PMC   4793893 . PMID   26108231.
  28. ↑ Martin, E. R.; Ritchie, M. D.; Hahn, L.; Kang, S.; Moore, J. H. (1 February 2006). "A novel method to identify gene-gene effects in nuclear families: the MDR-PDT". Genetic Epidemiology. 30 (2): 111–123. doi:10.1002/gepi.20128. ISSN   0741-0395. PMID   16374833. S2CID   25772215.
  29. ↑ Lou, Xiang-Yang; Chen, Guo-Bo; Yan, Lei; Ma, Jennie Z.; Mangold, Jamie E.; Zhu, Jun; Elston, Robert C.; Li, Ming D. (1 October 2008). "A combinatorial approach to detecting gene-gene and gene-environment interactions in family studies". American Journal of Human Genetics. 83 (4): 457–467. doi:10.1016/j.ajhg.2008.09.001. ISSN   1537-6605. PMC   2561932 . PMID   18834969.
  30. ↑ Cattaert, Tom; Urrea, Víctor; Naj, Adam C.; De Lobel, Lizzy; De Wit, Vanessa; Fu, Mao; Mahachie John, Jestinah M.; Shen, Haiqing; Calle, M. Luz (22 April 2010). "FAM-MDR: a flexible family-based multifactor dimensionality reduction technique to detect epistasis using related individuals". PLOS ONE. 5 (4): e10304. Bibcode:2010PLoSO...510304C. doi: 10.1371/journal.pone.0010304 . ISSN   1932-6203. PMC   2858665 . PMID   20421984.
  31. ↑ Leem, Sangseob; Park, Taesung (14 March 2017). "An empirical fuzzy multifactor dimensionality reduction method for detecting gene-gene interactions". BMC Genomics. 18 (Suppl 2): 115. doi: 10.1186/s12864-017-3496-x . ISSN   1471-2164. PMC   5374597 . PMID   28361694.
  32. ↑ Gui, Jiang; Andrew, Angeline S.; Andrews, Peter; Nelson, Heather M.; Kelsey, Karl T.; Karagas, Margaret R.; Moore, Jason H. (1 January 2010). "A simple and computationally efficient sampling approach to covariate adjustment for multifactor dimensionality reduction analysis of epistasis". Human Heredity. 70 (3): 219–225. doi:10.1159/000319175. ISSN   1423-0062. PMC   2982850 . PMID   20924193.
  33. ↑ Chung, Yujin; Lee, Seung Yeoun; Elston, Robert C.; Park, Taesung (1 January 2007). "Odds ratio based multifactor-dimensionality reduction method for detecting gene-gene interactions". Bioinformatics. 23 (1): 71–76. doi: 10.1093/bioinformatics/btl557 . ISSN   1367-4811. PMID   17092990.
  34. ↑ Dai, Hongying; Charnigo, Richard J.; Becker, Mara L.; Leeder, J. Steven; Motsinger-Reif, Alison A. (8 January 2013). "Risk score modeling of multiple gene to gene interactions using aggregated-multifactor dimensionality reduction". BioData Mining. 6 (1): 1. doi: 10.1186/1756-0381-6-1 . PMC   3560267 . PMID   23294634.
  35. ↑ Gui, Jiang; Moore, Jason H.; Kelsey, Karl T.; Marsit, Carmen J.; Karagas, Margaret R.; Andrew, Angeline S. (1 January 2011). "A novel survival multifactor dimensionality reduction method for detecting gene-gene interactions with application to bladder cancer prognosis". Human Genetics. 129 (1): 101–110. doi:10.1007/s00439-010-0905-5. ISSN   1432-1203. PMC   3255326 . PMID   20981448.
  36. ↑ Lee, Seungyeoun; Son, Donghee; Yu, Wenbao; Park, Taesung (1 December 2016). "Gene-Gene Interaction Analysis for the Accelerated Failure Time Model Using a Unified Model-Based Multifactor Dimensionality Reduction Method". Genomics & Informatics. 14 (4): 166–172. doi:10.5808/GI.2016.14.4.166. ISSN   1598-866X. PMC   5287120 . PMID   28154507.
  37. ↑ Gui, Jiang; Andrew, Angeline S.; Andrews, Peter; Nelson, Heather M.; Kelsey, Karl T.; Karagas, Margaret R.; Moore, Jason H. (1 January 2011). "A robust multifactor dimensionality reduction method for detecting gene-gene interactions with application to the genetic analysis of bladder cancer susceptibility". Annals of Human Genetics. 75 (1): 20–28. doi:10.1111/j.1469-1809.2010.00624.x. ISSN   1469-1809. PMC   3057873 . PMID   21091664.
  38. ↑ Gui, Jiang; Moore, Jason H.; Williams, Scott M.; Andrews, Peter; Hillege, Hans L.; van der Harst, Pim; Navis, Gerjan; Van Gilst, Wiek H.; Asselbergs, Folkert W. (1 January 2013). "A Simple and Computationally Efficient Approach to Multifactor Dimensionality Reduction Analysis of Gene-Gene Interactions for Quantitative Traits". PLOS ONE. 8 (6): e66545. Bibcode:2013PLoSO...866545G. doi: 10.1371/journal.pone.0066545 . ISSN   1932-6203. PMC   3689797 . PMID   23805232.
  39. ↑ Lou, Xiang-Yang; Chen, Guo-Bo; Yan, Lei; Ma, Jennie Z.; Zhu, Jun; Elston, Robert C.; Li, Ming D. (1 June 2007). "A generalized combinatorial approach for detecting gene-by-gene and gene-by-environment interactions with application to nicotine dependence". American Journal of Human Genetics. 80 (6): 1125–1137. doi:10.1086/518312. ISSN   0002-9297. PMC   1867100 . PMID   17503330.
  40. ↑ Tsai, Chia-Ti; Lai, Ling-Ping; Lin, Jiunn-Lee; Chiang, Fu-Tien; Hwang, Juey-Jen; Ritchie, Marylyn D.; Moore, Jason H.; Hsu, Kuan-Lih; Tseng, Chuen-Den (6 April 2004). "Renin-Angiotensin System Gene Polymorphisms and Atrial Fibrillation". Circulation. 109 (13): 1640–1646. doi: 10.1161/01.CIR.0000124487.36586.26 . ISSN   0009-7322. PMID   15023884.
  41. ↑ Asselbergs, Folkert W.; Moore, Jason H.; van den Berg, Maarten P.; Rimm, Eric B.; de Boer, Rudolf A.; Dullaart, Robin P.; Navis, Gerjan; van Gilst, Wiek H. (1 January 2006). "A role for CETP TaqIB polymorphism in determining susceptibility to atrial fibrillation: a nested case control study". BMC Medical Genetics. 7: 39. doi: 10.1186/1471-2350-7-39 . ISSN   1471-2350. PMC   1462991 . PMID   16623947.
  42. ↑ Ma, D.Q.; Whitehead, P.L.; Menold, M.M.; Martin, E.R.; Ashley-Koch, A.E.; Mei, H.; Ritchie, M.D.; DeLong, G.R.; Abramson, R.K. (1 September 2005). "Identification of Significant Association and Gene-Gene Interaction of GABA Receptor Subunit Genes in Autism". The American Journal of Human Genetics. 77 (3): 377–388. doi:10.1086/433195. ISSN   0002-9297. PMC   1226204 . PMID   16080114.
  43. ↑ Andrew, Angeline S.; Nelson, Heather H.; Kelsey, Karl T.; Moore, Jason H.; Meng, Alexis C.; Casella, Daniel P.; Tosteson, Tor D.; Schned, Alan R.; Karagas, Margaret R. (1 May 2006). "Concordance of multiple analytical approaches demonstrates a complex relationship between DNA repair gene SNPs, smoking and bladder cancer susceptibility". Carcinogenesis. 27 (5): 1030–1037. doi: 10.1093/carcin/bgi284 . ISSN   0143-3334. PMID   16311243.
  44. ↑ Andrew, Angeline S.; Karagas, Margaret R.; Nelson, Heather H.; Guarrera, Simonetta; Polidoro, Silvia; Gamberini, Sara; Sacerdote, Carlotta; Moore, Jason H.; Kelsey, Karl T. (1 January 2008). "DNA Repair Polymorphisms Modify Bladder Cancer Risk: A Multi-factor Analytic Strategy". Human Heredity. 65 (2): 105–118. doi:10.1159/000108942. ISSN   0001-5652. PMC   2857629 . PMID   17898541.
  45. ↑ Andrew, Angeline S.; Hu, Ting; Gu, Jian; Gui, Jiang; Ye, Yuanqing; Marsit, Carmen J.; Kelsey, Karl T.; Schned, Alan R.; Tanyos, Sam A. (1 January 2012). "HSD3B and gene-gene interactions in a pathway-based analysis of genetic susceptibility to bladder cancer". PLOS ONE. 7 (12): e51301. Bibcode:2012PLoSO...751301A. doi: 10.1371/journal.pone.0051301 . ISSN   1932-6203. PMC   3526593 . PMID   23284679.
  46. ↑ Cao, Jingjing; Luo, Chenglin; Yan, Rui; Peng, Rui; Wang, Kaijuan; Wang, Peng; Ye, Hua; Song, Chunhua (1 December 2016). "rs15869 at miRNA binding site in BRCA2 is associated with breast cancer susceptibility". Medical Oncology. 33 (12): 135. doi:10.1007/s12032-016-0849-2. ISSN   1357-0560. PMID   27807724. S2CID   26042128.
  47. ↑ Williams, Scott M.; Ritchie, Marylyn D.; III, John A. Phillips; Dawson, Elliot; Prince, Melissa; Dzhura, Elvira; Willis, Alecia; Semenya, Amma; Summar, Marshall (1 January 2004). "Multilocus Analysis of Hypertension: A Hierarchical Approach". Human Heredity. 57 (1): 28–38. doi:10.1159/000077387. ISSN   0001-5652. PMID   15133310. S2CID   21079485.
  48. ↑ Sanada, Hironobu; Yatabe, Junichi; Midorikawa, Sanae; Hashimoto, Shigeatsu; Watanabe, Tsuyoshi; Moore, Jason H.; Ritchie, Marylyn D.; Williams, Scott M.; Pezzullo, John C. (1 March 2006). "Single-Nucleotide Polymorphisms for Diagnosis of Salt-Sensitive Hypertension". Clinical Chemistry. 52 (3): 352–360. doi: 10.1373/clinchem.2005.059139 . ISSN   0009-9147. PMID   16439609.
  49. ↑ Moore, Jason H.; Williams, Scott M. (1 January 2002). "New strategies for identifying gene-gene interactions in hypertension". Annals of Medicine. 34 (2): 88–95. doi:10.1080/07853890252953473. ISSN   0785-3890. PMID   12108579. S2CID   25398042.
  50. ↑ De, Rishika; Verma, Shefali S.; Holzinger, Emily; Hall, Molly; Burt, Amber; Carrell, David S.; Crosslin, David R.; Jarvik, Gail P.; Kuivaniemi, Helena (1 February 2017). "Identifying gene-gene interactions that are highly associated with four quantitative lipid traits across multiple cohorts" (PDF). Human Genetics. 136 (2): 165–178. doi:10.1007/s00439-016-1738-7. ISSN   1432-1203. PMID   27848076. S2CID   24702049.
  51. ↑ De, Rishika; Verma, Shefali S.; Drenos, Fotios; Holzinger, Emily R.; Holmes, Michael V.; Hall, Molly A.; Crosslin, David R.; Carrell, David S.; Hakonarson, Hakon (1 January 2015). "Identifying gene-gene interactions that are highly associated with Body Mass Index using Quantitative Multifactor Dimensionality Reduction (QMDR)". BioData Mining. 8: 41. doi: 10.1186/s13040-015-0074-0 . PMC   4678717 . PMID   26674805.
  52. ↑ Duell, Eric J.; Bracci, Paige M.; Moore, Jason H.; Burk, Robert D.; Kelsey, Karl T.; Holly, Elizabeth A. (1 June 2008). "Detecting pathway-based gene-gene and gene-environment interactions in pancreatic cancer". Cancer Epidemiology, Biomarkers & Prevention. 17 (6): 1470–1479. doi:10.1158/1055-9965.EPI-07-2797. ISSN   1055-9965. PMC   4410856 . PMID   18559563.
  53. ↑ Xu, Jianfeng; Lowey, James; Wiklund, Fredrik; Sun, Jielin; Lindmark, Fredrik; Hsu, Fang-Chi; Dimitrov, Latchezar; Chang, Baoli; Turner, Aubrey R. (1 November 2005). "The Interaction of Four Genes in the Inflammation Pathway Significantly Predicts Prostate Cancer Risk". Cancer Epidemiology, Biomarkers & Prevention. 14 (11): 2563–2568. doi: 10.1158/1055-9965.EPI-05-0356 . ISSN   1055-9965. PMID   16284379.
  54. ↑ Lavender, Nicole A.; Rogers, Erica N.; Yeyeodu, Susan; Rudd, James; Hu, Ting; Zhang, Jie; Brock, Guy N.; Kimbro, Kevin S.; Moore, Jason H. (30 April 2012). "Interaction among apoptosis-associated sequence variants and joint effects on aggressive prostate cancer". BMC Medical Genomics. 5: 11. doi: 10.1186/1755-8794-5-11 . ISSN   1755-8794. PMC   3355002 . PMID   22546513.
  55. ↑ Lavender, Nicole A.; Benford, Marnita L.; VanCleave, Tiva T.; Brock, Guy N.; Kittles, Rick A.; Moore, Jason H.; Hein, David W.; Kidd, La Creis R. (16 November 2009). "Examination of polymorphic glutathione S-transferase (GST) genes, tobacco smoking and prostate cancer risk among men of African descent: a case-control study". BMC Cancer. 9: 397. doi: 10.1186/1471-2407-9-397 . ISSN   1471-2407. PMC   2783040 . PMID   19917083.
  56. ↑ Collins, Ryan L.; Hu, Ting; Wejse, Christian; Sirugo, Giorgio; Williams, Scott M.; Moore, Jason H. (18 February 2013). "Multifactor dimensionality reduction reveals a three-locus epistatic interaction associated with susceptibility to pulmonary tuberculosis". BioData Mining. 6 (1): 4. doi: 10.1186/1756-0381-6-4 . PMC   3618340 . PMID   23418869.
  57. ↑ Wilke, Russell A.; Reif, David M.; Moore, Jason H. (1 November 2005). "Combinatorial Pharmacogenetics". Nature Reviews Drug Discovery. 4 (11): 911–918. doi:10.1038/nrd1874. ISSN   1474-1776. PMID   16264434. S2CID   11643026.
  58. ↑ Motsinger, Alison A.; Ritchie, Marylyn D.; Shafer, Robert W.; Robbins, Gregory K.; Morse, Gene D.; Labbe, Line; Wilkinson, Grant R.; Clifford, David B.; D'Aquila, Richard T. (1 November 2006). "Multilocus genetic interactions and response to efavirenz-containing regimens: an adult AIDS clinical trials group study". Pharmacogenetics and Genomics. 16 (11): 837–845. doi:10.1097/01.fpc.0000230413.97596.fa. ISSN   1744-6872. PMID   17047492. S2CID   26266170.
  59. ↑ Ritchie, Marylyn D.; Motsinger, Alison A. (1 December 2005). "Multifactor dimensionality reduction for detecting gene-gene and gene-environment interactions in pharmacogenomics studies". Pharmacogenomics. 6 (8): 823–834. doi:10.2217/14622416.6.8.823. ISSN   1462-2416. PMID   16296945. S2CID   10348021.
  60. ↑ Moore, Jason H.; Asselbergs, Folkert W.; Williams, Scott M. (15 February 2010). "Bioinformatics challenges for genome-wide association studies". Bioinformatics. 26 (4): 445–455. doi:10.1093/bioinformatics/btp713. ISSN   1367-4811. PMC   2820680 . PMID   20053841.
  61. ↑ Sun, Xiangqing; Lu, Qing; Mukherjee, Shubhabrata; Mukheerjee, Shubhabrata; Crane, Paul K.; Elston, Robert; Ritchie, Marylyn D. (1 January 2014). "Analysis pipeline for the epistasis search – statistical versus biological filtering". Frontiers in Genetics. 5: 106. doi: 10.3389/fgene.2014.00106 . PMC   4012196 . PMID   24817878.
  62. ↑ Pendergrass, Sarah A.; Frase, Alex; Wallace, John; Wolfe, Daniel; Katiyar, Neerja; Moore, Carrie; Ritchie, Marylyn D. (30 December 2013). "Genomic analyses with biofilter 2.0: knowledge driven filtering, annotation, and model development". BioData Mining. 6 (1): 25. doi: 10.1186/1756-0381-6-25 . PMC   3917600 . PMID   24378202.
  63. ↑ Moore, Jason H. (1 January 2015). "Epistasis Analysis Using ReliefF". Epistasis. Methods in Molecular Biology. Vol. 1253. pp. 315–325. doi:10.1007/978-1-4939-2155-3_17. ISBN   978-1-4939-2154-6. ISSN   1940-6029. PMID   25403540.
  64. ↑ Moore, Jason H.; White, Bill C. (1 January 2007). "Genome-Wide Genetic Analysis Using Genetic Programming: The Critical Need for Expert Knowledge". In Riolo, Rick; Soule, Terence; Worzel, Bill (eds.). Genetic Programming Theory and Practice IV. Genetic and Evolutionary Computation. Springer US. pp. 11–28. doi:10.1007/978-0-387-49650-4_2. ISBN   9780387333755. S2CID   55188394.
  65. ↑ Greene, Casey S.; Sinnott-Armstrong, Nicholas A.; Himmelstein, Daniel S.; Park, Paul J.; Moore, Jason H.; Harris, Brent T. (1 March 2010). "Multifactor dimensionality reduction for graphics processing units enables genome-wide testing of epistasis in sporadic ALS". Bioinformatics. 26 (5): 694–695. doi:10.1093/bioinformatics/btq009. ISSN   1367-4811. PMC   2828117 . PMID   20081222.
  66. ↑ Bush, William S.; Dudek, Scott M.; Ritchie, Marylyn D. (1 September 2006). "Parallel multifactor dimensionality reduction: a tool for the large-scale analysis of gene-gene interactions". Bioinformatics. 22 (17): 2173–2174. doi:10.1093/bioinformatics/btl347. ISSN   1367-4811. PMC   4939609 . PMID   16809395.
  67. ↑ Sinnott-Armstrong, Nicholas A.; Greene, Casey S.; Cancare, Fabio; Moore, Jason H. (24 July 2009). "Accelerating epistasis analysis in human genetics with consumer graphics hardware". BMC Research Notes. 2: 149. doi: 10.1186/1756-0500-2-149 . ISSN   1756-0500. PMC   2732631 . PMID   19630950.
  68. ↑ Winham, Stacey J.; Motsinger-Reif, Alison A. (16 August 2011). "An R package implementation of multifactor dimensionality reduction". BioData Mining. 4 (1): 24. doi: 10.1186/1756-0381-4-24 . ISSN   1756-0381. PMC   3177775 . PMID   21846375.
  69. ↑ Calle, M. Luz; Urrea, Víctor; Malats, Núria; Van Steen, Kristel (1 September 2010). "mbmdr: an R package for exploring gene-gene interactions associated with binary or quantitative traits". Bioinformatics. 26 (17): 2198–2199. doi: 10.1093/bioinformatics/btq352 . ISSN   1367-4811. PMID   20595460.

Further reading

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.