The Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by French engineer and physicist Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, when no one realized that the waves were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.

Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes or metamaterials.

A metamaterial is any material engineered to have a property that is rarely observed in naturally occurring materials. They are made from assemblies of multiple elements fashioned from composite materials such as metals and plastics. These materials are usually arranged in repeating patterns, at scales that are smaller than the wavelengths of the phenomena they influence. Metamaterials derive their properties not from the properties of the base materials, but from their newly designed structures. Their precise shape, geometry, size, orientation and arrangement gives them their smart properties capable of manipulating electromagnetic waves: by blocking, absorbing, enhancing, or bending waves, to achieve benefits that go beyond what is possible with conventional materials.
In particle theory, the skyrmion is a topologically stable field configuration of a certain class of non-linear sigma models. It was originally proposed as a model of the nucleon by Tony Skyrme in 1961. As a topological soliton in the pion field, it has the remarkable property of being able to model, with reasonable accuracy, multiple low-energy properties of the nucleon, simply by fixing the nucleon radius. It has since found application in solid-state physics, as well as having ties to certain areas of string theory.

Victor Georgievich Veselago was a Soviet Russian physicist, doctor of physical and mathematical sciences, and a university professor. In 1967, he was the first to publish a theoretical analysis of materials with negative permittivity, ε, and permeability, μ.
In crystal optics, the index ellipsoid is a geometric construction which concisely represents the refractive indices and associated polarizations of light, as functions of the orientation of the wavefront, in a doubly-refractive crystal. When this ellipsoid is cut through its center by a plane parallel to the wavefront, the resulting intersection is an ellipse whose major and minor semiaxes have lengths equal to the two refractive indices for that orientation of the wavefront, and have the directions of the respective polarizations as expressed by the electric displacement vector D. The principal semiaxes of the index ellipsoid are called the principal refractive indices.

A split-ring resonator (SRR) is an artificially produced structure common to metamaterials. Its purpose is to produce the desired magnetic susceptibility in various types of metamaterials up to 200 terahertz.
In physics, engineering and materials science, bi-isotropic materials have the special optical property that they can rotate the polarization of light in either refraction or transmission. This does not mean all materials with twist effect fall in the bi-isotropic class. The twist effect of the class of bi-isotropic materials is caused by the chirality and non-reciprocity of the structure of the media, in which the electric and magnetic field of an electromagnetic wave interact in an unusual way.

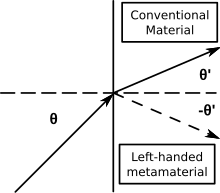
Negative-index metamaterial or negative-index material (NIM) is a metamaterial whose refractive index for an electromagnetic wave has a negative value over some frequency range.

Metamaterial antennas are a class of antennas which use metamaterials to increase performance of miniaturized antenna systems. Their purpose, as with any electromagnetic antenna, is to launch energy into free space. However, this class of antenna incorporates metamaterials, which are materials engineered with novel, often microscopic, structures to produce unusual physical properties. Antenna designs incorporating metamaterials can step-up the antenna's radiated power.

An acoustic metamaterial, sonic crystal, or phononic crystal is a material designed to control, direct, and manipulate sound waves or phonons in gases, liquids, and solids. Sound wave control is accomplished through manipulating parameters such as the bulk modulus β, density ρ, and chirality. They can be engineered to either transmit, or trap and amplify sound waves at certain frequencies. In the latter case, the material is an acoustic resonator.

A photonic metamaterial (PM), also known as an optical metamaterial, is a type of electromagnetic metamaterial, that interacts with light, covering terahertz (THz), infrared (IR) or visible wavelengths. The materials employ a periodic, cellular structure.
A nonlinear metamaterial is an artificially constructed material that can exhibit properties not yet found in nature. Its response to electromagnetic radiation can be characterized by its permittivity and material permeability. The product of the permittivity and permeability results in the refractive index. Unlike natural materials, nonlinear metamaterials can produce a negative refractive index. These can also produce a more pronounced nonlinear response than naturally occurring materials.
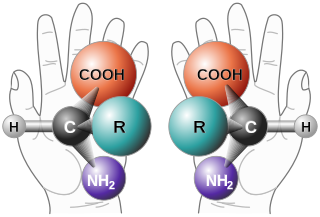
The term chiral describes an object, especially a molecule, which has or produces a non-superposable mirror image of itself. In chemistry, such a molecule is called an enantiomer or is said to exhibit chirality or enantiomerism. The term "chiral" comes from the Greek word for the human hand, which itself exhibits such non-superimposeability of the left hand precisely over the right. Due to the opposition of the fingers and thumbs, no matter how the two hands are oriented, it is impossible for both hands to exactly coincide. Helices, chiral characteristics (properties), chiral media, order, and symmetry all relate to the concept of left- and right-handedness.

The history of metamaterials begins with artificial dielectrics in microwave engineering as it developed just after World War II. Yet, there are seminal explorations of artificial materials for manipulating electromagnetic waves at the end of the 19th century. Hence, the history of metamaterials is essentially a history of developing certain types of manufactured materials, which interact at radio frequency, microwave, and later optical frequencies.
Dyakonov surface waves (DSWs) are surface electromagnetic waves that travel along the interface in between an isotropic and an uniaxial-birefringent medium. They were theoretically predicted in 1988 by the Russian physicist Mikhail Dyakonov. Unlike other types of acoustic and electromagnetic surface waves, the DSW's existence is due to the difference in symmetry of materials forming the interface. He considered the interface between an isotropic transmitting medium and an anisotropic uniaxial crystal, and showed that under certain conditions waves localized at the interface should exist. Later, similar waves were predicted to exist at the interface between two identical uniaxial crystals with different orientations. The previously known electromagnetic surface waves, surface plasmons and surface plasmon polaritons, exist under the condition that the permittivity of one of the materials forming the interface is negative, while the other one is positive. In contrast, the DSW can propagate when both materials are transparent; hence they are virtually lossless, which is their most fascinating property.
In optics, the Ewald–Oseen extinction theorem, sometimes referred to as just the extinction theorem, is a theorem that underlies the common understanding of scattering. It is named after Paul Peter Ewald and Carl Wilhelm Oseen, who proved the theorem in crystalline and isotropic media, respectively, in 1916 and 1915. Originally, the theorem applied to scattering by an isotropic dielectric objects in free space. The scope of the theorem was greatly extended to encompass a wide variety of bianisotropic media.
In the physics of continuous media, spatial dispersion is usually described as a phenomenon where material parameters such as permittivity or conductivity have dependence on wavevector. Normally, such a dependence is assumed to be absent for simplicity, however spatial dispersion exists to varying degrees in all materials.

Sergei Anatolyevich Tretyakov is a Russian-Finnish scientist, focused in electromagnetic field theory, complex media electromagnetics and microwave engineering. He is currently a professor at Department of Electronics and Nanoengineering, Aalto University, Finland. His main research area in recent years is metamaterials and metasurfaces from fundamentals to applications. He was the president of the European Virtual Institute for Artificial Electromagnetic Materials and Metamaterials and general chair of the Metamaterials Congresses from 2007 to 2013. He is a fellow/member of many scientific associations such as IEEE, URSI, the Electromagnetics Academy, and OSA. He is also an Honorary Doctor of Francisk Skorina Gomel State University.