
The astronomical unit is a unit of length defined to be exactly equal to 149,597,870,700 m. Historically, the astronomical unit was conceived as the average Earth-Sun distance, before its modern redefinition in 2012.
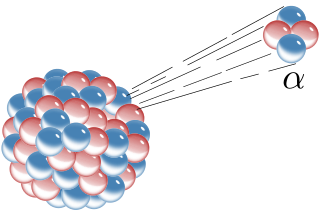
Alpha decay or α-decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle and thereby transforms or "decays" into a different atomic nucleus, with a mass number that is reduced by four and an atomic number that is reduced by two. An alpha particle is identical to the nucleus of a helium-4 atom, which consists of two protons and two neutrons. It has a charge of +2 e and a mass of 4 Da. For example, uranium-238 decays to form thorium-234.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.

Georg Ferdinand Ludwig Philipp Cantor was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Physics is a branch of science whose primary objects of study are matter and energy. Discoveries of physics find applications throughout the natural sciences and in technology. Historically, physics emerged from the scientific revolution of the 17th century, grew rapidly in the 19th century, then was transformed by a series of discoveries in the 20th century. Physics today may be divided loosely into classical physics and modern physics.

The second is the unit of time in the International System of Units (SI), historically defined as 1⁄86400 of a day – this factor derived from the division of the day first into 24 hours, then to 60 minutes and finally to 60 seconds each. "Minute" comes from the Latin pars minuta prima, meaning "first small part", and "second" comes from the pars minuta secunda, "second small part".

The cosmos is an alternative name for the universe or its nature or order. Usage of the word cosmos implies viewing the universe as a complex and orderly system or entity.

Eratosthenes of Cyrene was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to what is now known as the study of geography, and he introduced some of the terminology still used today.

George Gamow, sometimes Gammoff; born Georgiy Antonovich Gamov was a Soviet and American polymath, theoretical physicist and cosmologist. He was an early advocate and developer of Lemaître's Big Bang theory. Gamow discovered a theoretical explanation of alpha decay by quantum tunneling, invented the liquid drop model and the first mathematical model of the atomic nucleus, worked on radioactive decay, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, and molecular genetics.
In mathematics, transfinite numbers or infinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term transfinite was coined in 1895 by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term transfinite also remains in use.

The history of geodesy (/dʒiːˈɒdɪsi/) began during antiquity and ultimately blossomed during the Age of Enlightenment.

In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph (ℵ).
The timeline below shows the date of publication of possible major scientific breakthroughs, theories and discoveries, along with the discoverer. This article discounts mere speculation as discovery, although imperfect reasoned arguments, arguments based on elegance/simplicity, and numerically/experimentally verified conjectures qualify. The timeline begins at the Bronze Age, as it is difficult to give even estimates for the timing of events prior to this, such as of the discovery of counting, natural numbers and arithmetic.

White Light is a work of science fiction by Rudy Rucker published in 1980 by Virgin Books in the UK and Ace Books in the US. It was written while Rucker was teaching mathematics at the University of Heidelberg from 1978 to 1980, at roughly the same time he was working on the non-fiction book Infinity and the Mind.

Fredrik Carl Mülertz Størmer was a Norwegian mathematician and astrophysicist. In mathematics, he is known for his work in number theory, including the calculation of π and Størmer's theorem on consecutive smooth numbers. In physics, he is known for studying the movement of charged particles in the magnetosphere and the formation of aurorae, and for his book on these subjects, From the Depths of Space to the Heart of the Atom. He worked for many years as a professor of mathematics at the University of Oslo in Norway. A crater on the far side of the Moon is named after him.
In philosophy and theology, infinity is explored in articles under headings such as the Absolute, God, and Zeno's paradoxes.

Infinity is something which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .

Jorge Luis Borges and mathematics concerns several modern mathematical concepts found in certain essays and short stories of Argentinian author Jorge Luis Borges (1899–1986), including concepts such as set theory, recursion, chaos theory, and infinite sequences, although Borges' strongest links to mathematics are through Georg Cantor's theory of infinite sets, outlined in "The Doctrine of Cycles". Some of Borges' most popular works such as "The Library of Babel", "The Garden of Forking Paths", "The Aleph", an allusion to Cantor's use of the Hebrew letter aleph to denote cardinality of transfinite sets, and "The Approach to Al-Mu'tasim" illustrate his use of mathematics.

Beyond Infinity : An Expedition to the Outer Limits of Mathematics is a popular mathematics book by Eugenia Cheng centered on concepts of infinity. It was published by Basic Books and by Profile Books in 2017, and in a paperback edition in 2018. It was shortlisted for the 2017 Royal Society Insight Investment Science Book Prize.
From Zero to Infinity: What Makes Numbers Interesting is a book in popular mathematics and number theory by Constance Reid. It was originally published in 1955 by the Thomas Y. Crowell Company. The fourth edition was published in 1992 by the Mathematical Association of America in their MAA Spectrum series. A K Peters published a fifth "Fiftieth anniversary edition" in 2006.


















