Related Research Articles

Sir Andrew John Wiles is an English mathematician and a Royal Society Research Professor at the University of Oxford, specialising in number theory. He is best known for proving Fermat's Last Theorem, for which he was awarded the 2016 Abel Prize and the 2017 Copley Medal by the Royal Society. He was appointed Knight Commander of the Order of the British Empire in 2000, and in 2018, was appointed the first Regius Professor of Mathematics at Oxford. Wiles is also a 1997 MacArthur Fellow.

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain.

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations.
Kenneth Ira Appel was an American mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana–Champaign, solved one of the most famous problems in mathematics, the four-color theorem. They proved that any two-dimensional map, with certain limitations, can be filled in with four colors without any adjacent "countries" sharing the same color.

Wolfgang Haken was a German American mathematician who specialized in topology, in particular 3-manifolds.
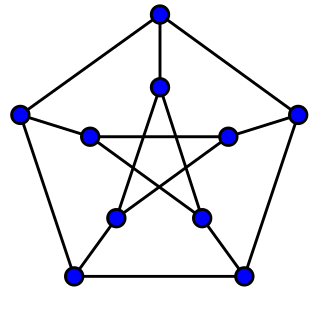
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.

In mathematics, the Heawood number of a surface is an upper bound for the number of colors that suffice to color any graph embedded in the surface.

In mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of points on a graph with alternating colors.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most Δ+µ colors, where µ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.
The discharging method is a technique used to prove lemmas in structural graph theory. Discharging is most well known for its central role in the proof of the four color theorem. The discharging method is used to prove that every graph in a certain class contains some subgraph from a specified list. The presence of the desired subgraph is then often used to prove a coloring result.
The problem in number theory known as "Fermat's Last Theorem" has repeatedly received attention in fiction and popular culture. The theorem was proved by Andrew Wiles in 1994.

In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c satisfy the equation an + bn = cn for any integer value of n greater than 2. The cases n = 1 and n = 2 have been known since antiquity to have infinitely many solutions.
The following is a timeline of scientific computing, also known as computational science.
This is a timeline of key developments in computational mathematics.
Dorothea Blostein is a Canadian computer scientist who works as a professor of computer science at Queen's University. She has published well-cited publications on computer vision,[BA] image analysis,[ZBC] and graph rewriting,[BFG] and is known as one of the authors of the master theorem for divide-and-conquer recurrences.[BHS] Her research interests also include biomechanics and tensegrity.

The Illinois Journal of Mathematics is a quarterly peer-reviewed scientific journal of mathematics published by Duke University Press on behalf of the University of Illinois. It was established in 1957 by Reinhold Baer, Joseph L. Doob, Abraham Taub, George W. Whitehead, and Oscar Zariski.
References
- ↑ Faltings, Gerd (July 1995), "The Proof of Fermat's Last Theorem by R. Taylor and A. Wiles" (PDF), Notices of the AMS, 42 (7): 743–746, ISSN 0002-9920
- ↑ K. Appel and W. Haken (1977), "Every planar map is four colorable. Part I. Discharging", Illinois J. Math21: 429–490. MR 543795
- ↑ K. Appel, W. Haken, and J. Koch (1977), "Every planar map is four colorable. Part II. Reducibility", Illinois J. Math21: 491–567. MR 543795
- ↑ Vendruscolo, M.; Najmanovich, R.; Domany, E. (1999), "Protein Folding in Contact Map Space", Physical Review Letters, 82 (3): 656–659, arXiv: cond-mat/9901215 , Bibcode:1999PhRvL..82..656V, doi:10.1103/PhysRevLett.82.656, S2CID 6686420
- ↑ Dill, K.A.; Ozkan, S.B.; Weikl, T.R.; Chodera, J.D.; Voelz, V.A. (2007), "The protein folding problem: when will it be solved?" (PDF), Current Opinion in Structural Biology, 17 (3): 342–346, doi:10.1016/j.sbi.2007.06.001, PMID 17572080, archived from the original (PDF) on 2011-07-20